Теоретическая механика. ТеорМех. Примеры. Методические рекомендации по решению задач

• Название: Методические рекомендации по решению задач
• Анкор: Теоретическая механика
• Дата: 20.10.2020
• Размер: 317.36 Kb.
• Имя файла: ТеорМех. Примеры.docx
• Тип: Методические рекомендации; #144413
• страница: 1 из 3

Методические рекомендации по решению задач

Рассмотрим, что может быть целью кинематических задач.

1. Нас может интересовать изменение кинематических величин в процессе движения, т.е. получение сведений об изменении координат, скорости, ускорения, а также соответствующих угловых величин.

2. В ряде задач, например, в задаче о движении тела под углом к горизонту, требуется узнать о значениях физических величин в конкретных состояниях: дальности полета, наибольшей величине подъема и т.д.

3. В случаях, когда тело одновременно участвует в нескольких движениях (например, качение шара) или рассматривается относительное движение нескольких тел, возникает необходимость установить соотношения между перемещениями, скоростями и ускорениями (линейными и угловыми), т.е. найти уравнения кинематической связи.

Несмотря на большое разнообразие задач по кинематике, можно предложить следующий алгоритм их решения:

1. Сделать схематический рисунок, изобразив начальное положение тел и их начальное состояние, т.е.   и   .

2. Выбрать систему отсчета на основании анализа условия задачи. Для этого нужно выбрать тело отсчета и связать с ним систему координат, указав начало отсчета координат, направление осей координат, момент начала отсчета времени. При выборе положительных направлений руководствуются направлением движения (скорости) или направлением ускорения.

3. Составить на основании законов движения систему уравнений в векторном виде для всех тел, а затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений следует обратить внимание на знаки "+" и "-" проекций входящих в них векторных величин.

4. Ответ необходимо получить в виде аналитической формулы (в общем виде), а в конце произвести числовые расчеты.

 

Пример 4. Даны уравнения движения точки х = 3t;  y=9t^2--4; где х, у - в см, t - в с. Найти уравнение траектории точки и для момента времени t₁ = 1с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение. Уравнения движения точки можно рассматривать как параметрические уравнения ее траектории. Чтобы получить уравнения траектории точки в координатной форме, исключим время t из уравнений ее движения



Траекторией точки является парабола.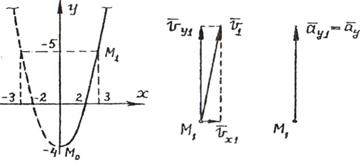



Приt₀= 0 иt₁= 1 с соответственно получаем точки М₀(0,- 4) и М₁(3,5).

Скорость и ускорение точки

v_х= = 3 [см/с];  

v_у =  = 18t [см/с];

а_х=   = 0;

а_у =  = 18 [см/с²].

Заметим, чтоv_x, а_х и а_у не зависят от времени t.

При t_l= 1 с получаем





Касательное и нормальное ускорения точки приt₁= 1 с





На рисунке показано положение точки М в заданный момент времени(t₁ = 1 с), а также выполнено построение векторов скорости и ускорения точки. Вектор  ₁ построен по составляющим   и  ; этот вектор совпадает по направлению с направлением касательной к траектории. Вектор  , построен по составляющим  и   .

Радиус кривизны траектории при t₁ = 1 с



Расчеты показывают, что радиус кривизны траектории в точке М₀(0,4) при t₀ = 0, ρ₀ = 0,5 [см].

 

Пример 5. Локомотив движется со скоростью 54 км/ч. При торможении он приобретает ускорение 0,5 м/с². Найти, на каком расстоянии от пункта остановки надо начать торможение и сколько време­ни оно будет продолжаться.

Решение. Локомотив, принятый за точку, совершает равнозамедленное движение в соответствии с уравнениями



Используя условия задачи, получим



где v₀= 54 [км/ч] = 15 [м/с];    а = 0,5 [м/с²];s₀= 0.

Из составленной системы уравнений находим время остановки и путь остановки локомотива





 

Пример 6. Сколько времени пассажир, сидящий у окна поезда, который идет со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, а длина 250 м?

Дано: 

Найти: t.



Решение. Неподвижную систему отсчета свяжем с Землей, подвижную – с поездом, в котором находится пассажир. Согласно закону сложения скоростей  , где   - скорость встречного поезда относительно первого. В проекциях на ось Ох:

.

Так как путь, пройденный встречным поездом относительно первого, равен длине поезда, то время

 ,  t=10 c.

 

Пример 7. Пароход идет от Нижнего Новгорода до Астрахани 5,0 суток, а обратно - 7,0 суток. Как долго будет плыть плот от Нижнего Новгорода до Астрахани? Стоянки и задержки в движении исключить.

Дано: t₁=5 сут, t₂=7 сут.

Найти: t₃



Решение. Неподвижную систему отсчета свяжем с берегом, подвижную – с водой. Будем считать, что скорость воды на всем пути одинакова и скорость парохода относительно воды постоянна и равна модулю мгновенной скорости парохода относительно воды.

Так как плот движется относительно берега со скоростью течения реки  , то время его движения  , где s – расстояние между городами. При движении парохода по течению его скорость согласно закону сложения скоростей  , или в проекциях на ось Ох:

                                                                                                                (1)

где   - скорость парохода относительно берега,   - скорость парохода относительно реки.

Зная время движения, можно найти скорость:

                                                                                                                          (2)

Из формул (1) и (2) имеем:

                                                                                                                 (3)

При движении парохода против течения  , или в проекциях на ось Ох  , где   - скорость парохода относительно берега.



С другой стороны,  . Тогда

                                                                                                                 (4)

Решая систему уравнений (3) и (4) относительно  , получим:



Найдем время движения плота:



t₃=35 сут.

 

Пример 8. При равноускоренном движении тело проходит за два первых равных последовательных промежутка времени по 4,0 с каждый пути s₁ = 24 м и s₂=64 м соответственно. Определите начальную скорость и ускорение тела.

Дано: t₁=t₂= 4,0 с, s₁ =24 м, s₂ = 64 м.

Найти:  .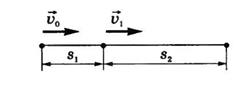



Решение. Запишем уравнения пути для s₁ и (s₁+s₂) соответственно. Так как начальная скорость в этом случае одинакова, то


                                               

Так как t1=t2, то

                                                            (2)

Выразив из (1)   и подставив ее в (2), получим:



Тогда начальная скорость 

 

Пример 9. Автомобиль, двигаясь по прямолинейной траектории равноускоренно с начальной скоростью 5,0 м/с, прошел за первую секунду путь, равный 6,0 м. Найдите ускорение автомобиля, мгновенную скорость в конце второй секунды и перемещение за 2,0 с.

Дано: 

Найти: 

Решение. Зная путь, пройденный телом за первую секунду, можно найти ускорение:



Скорость в конце второй секунды найдем по формуле



Перемещение за 2 с можно рассчитать по формулам:



Пример 10. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x = A + Bt + Ct³, где А=4 м, В=2м/с, С=-0,5 м/с³.

Для момента времени t₁=2 c определить: 1) координату точки х₁  точки; 2) мгновенную скорость v₁; 3) мгновенное ускорение а₁.

Дано: x = A + Bt + Ct³, А=4 м, В=2 м/с, С=-0,5 м/с³, t₁=2 c.

Найти: х₁; v₁; а₁.

Решение. 1.Подставим в уравнение движения вместо t заданное значение времени t₁:  x₁ = A + Bt₁ + Ct₁³. Подставим в это выражение значения А, В, С, t₁ и произведем вычисления:  х₁ = 4 м.

2. Мгновенная скорость:   Тогда в момент времени t₁ мгновенная скорость v₁ = B + 3Ct₁². Подставим сюда значения В,С, t₁:   v₁= – 4 м/с. Знак минус указывает на то, что в момент времени  t₁=2 c  точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение:   Мгновенное ускорение в момент времени t₁ равно а₁ = 6Сt₁.  Подставим значения С, t₁: а₁= –6 м/с². Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

 

Пример 11. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = A + Bt + Ct², где А=5 м,  В=4м/с,  С= -1м/с². Определить среднюю скорость v_хср за интервал времени от t₁=1 c до t₂=6 c.

Дано: х = A + Bt + Ct² , А=5м, В=4м/с, С=- 1м/с², t₁=1 c , t₂=6 c.

Найти: v_хср -?   а_хср -?

Решение. Средняя скорость за интервал времени t₂-t₁ определяется выражением v_ср=(х₂-х₁)/(t₂- t₁).

х₁ = A + Bt₁ + Ct₁²= 8 м,        х₂ = A + Bt₂ + Ct₂²= –7 м.

Подставим значения х₁, х₂, t₁ , t₂  и произведем вычисления: v_хср= 3 м/с.

 

Пример 12. Из вертолета,  находящегося на высоте h = 300 м, сбросили груз. Через какое время груз достигнет земли, если: а) вертолет неподвижен; б) вертолет опускается  со скоростью v₀=5 м/с;  3) вертолет поднимается со скоростью v₀=5 м/с. Описать графически соответствующие движения груза в осях s(t), v(t) и a(t).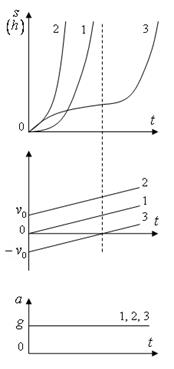



Решение. а) Груз, покинувший неподвижный вертолет, свободно падает, т.е. движется равноускоренно с ускорением свободного падения g. Время движения найдем из соотношения    Откуда    Графики движение объекта отмечены 1 на рисунке.

б) Движение груза, покинувшего вертолет, который опускается с постоянной скоростью v₀=5 м/с, является равноускоренным движением с постоянным ускорением g и описывается уравнением



Подстановка численных значений дает уравнение 9,8t²+10t-600=0.



Отрицательный результат не имеет физического смысла, поэтому время движения t=7,57 с.

Графики движение объекта отмечены 2 на рисунке.

3) Движение груза, покинувшего вертолет, который поднимается с постоянной скоростью v₀=5 м/с, cостоит из двух этапов. На первом  этапе – груз движется равнозамедленно с постоянным ускорением g, направленным противоположно скорости,  и описывается уравнениями



В верхней точке траектории скорость становится равной нулю, поэтому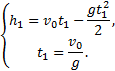



Подставляя второе уравнение системы в первое, получим



На втором этапе  – свободное падение с высоты h₀=h+h₁=300+1,28=301,28 м. 

Поскольку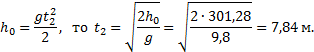



Графики движение объекта отмечены 3 на рисунке.