Реферат. Управление поставками и сбытом на предприятии к.р. Методические рекомендации по выполнению контрольной работы для студентов заочной формы обучения по дисциплине
 Скачать 1.92 Mb. Скачать 1.92 Mb.
|
|
Система с фиксированным интервалом времени между заказами Система с фиксированным интервалом времени между заказами — вторая и последняя система управления запасами, которая относится к основным. Классификация систем на основные и прочие вызвана тем, что две рассматриваемые системы лежат в основе всевозможных иных систем управления запасами. В системе с фиксированным интервалом времени между заказами, как ясно из названия, заказы делаются в строго определенные моменты времени, которые отстоят друг от друга на равные интервалы, например один раз в месяц, один раз в неделю, один раз в 14 дней и т. п. Следует только отметить особенности этой системы: - момент выдачи заявки определяется по достижению соответствующей даты, т.е., в отличие от рассмотренной выше системы, в данном случае контролируются не запасы, а время. -размер партии заказа в каждом цикле рассчитывается исходя из стремления после получения очередной партии иметь первоначально определенный максимальный размер запаса. Исходные данные для расчета параметров системы и их обозначения принимаем аналогичными данным ранее спроектированной системы. Гарантийный (страховой) запас позволяет обеспечивать потребность на время предполагаемой задержки поставки и рассчитывается следующим образом: Qстрах = Sп х Тз = 10 х 2 = 20 Максимальный запас рассчитывается исходя из условия получения всегда партии в размере ОРЗ: Qmax = Qстрах + ОРЗ = 20 + 100 = 120 Полученная партия ( ОРЗ ) расходуется полностью за 10 дней: ОРЗ : Sп = 100 : 10 = 10 Как видим, эти расчеты повторяют определение аналогичных параметров для системы с фиксированным размером заказа. Порядок дальнейших рассуждений при проектировании системы следующий ( рис. 4 ) – первый цикл ее работы : - Когда выдается заявка на пополнение запаса? Тогда, когда время придет ( дата контроля запасов и выдачи заявки ). Так, если первая полученная партия расходуется за 10 дней, а время выполнения заказа составляет 3 дня, то точка контроля должна быть за три дня до поставки, т.е. через 7 дней после первого пополнения запаса ( 10 – 3 = 7 ). - Когда придет новый заказ? Через 3 дня ( при отсутствии задержки ). Итого, от начала расходования запаса до момента получения новой партии пройдет 10 дней ( 7 + 3 ) = 10. - Какова величина запаса, при которой наступает плановая поставка новой партии? Эта величина определяется как разность между текущим запасом в точке контроля ( Qтек ) и запасом, потребленным за время ожидания заказа: ( Qтек – Sп х Т ). При этом текущий запас равен разности между Qмакс и запасом, израсходованным при работе до точки контроля ( 120 – 10 х 7 = 50 ). Следовательно, поставка новой партии происходит при достижении запасом значения 20 штук ( 50 – 10 х 3 = 20 ), т.е. страхового запаса. 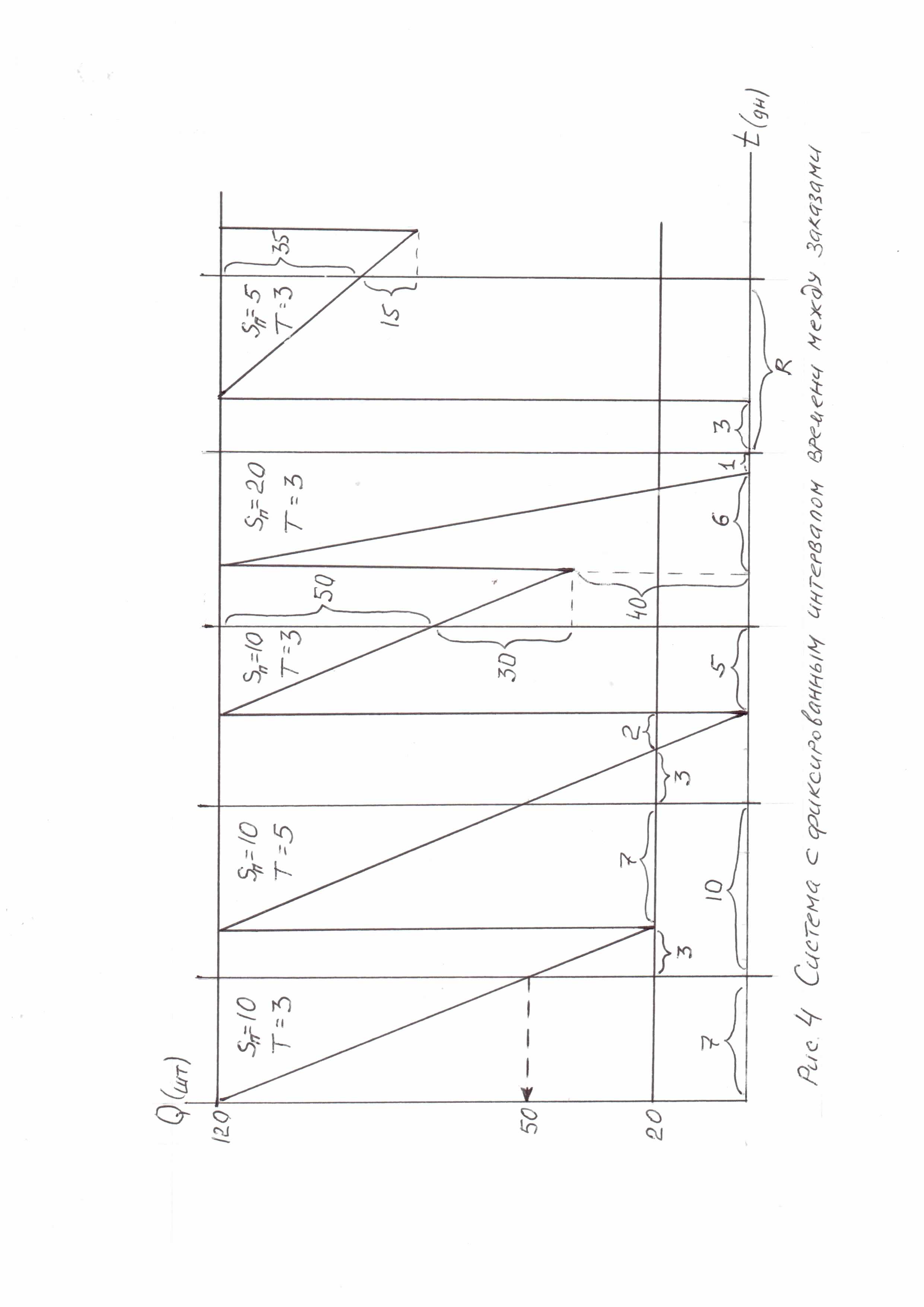 -Каков буде максимальный запас при поступлении заказа? Как указывалось выше, размер партии заказа в каждом цикле рассчитывается исходя из стремления после получения очередной партии иметь первоначально определенный максимальный размер запаса. В этом случае определение системой размера партии заказа состоит из суммирования размеров запаса, потребленного до точки контроля ( Qмакс –Qтек ), и запаса, который будет израсходован за время ожидания поставки ( Т х Sп ): Qзаказа = Qмакс – Qтек + Т х Sп = 120 – 50 + 3 х 10 = 100. Данными расчетами мы подтвердили тот очевидный факт, что при плановых значениях параметров системы, размер партии заказа равен ОРЗ. В этом случае, как и требуется, запас при получении партии достигнет значения 120 штук ( 20 + 100 = 120 ). - Когда наступит время для следующей точки контроля и выдачи заявки? Другими словами, чему равен фиксированный интервал времени между заказами ( R )? По графику несложно понять, что он равен времени расходования ОРЗ при плановом потреблении : R = ОРЗ : Sп = 100 : 10 = 10 дней. Проведем анализ реакции системы с фиксированным интервалом времени между заказами на ряд типовых сбоев. 1. . Задержка поставки партии ( прогнозируемый сбой ) при плановом потреблении: Sп = 10; Т = 5 ( Второй цикл работы системы на рис.4 ). - Когда выдается заявка на пополнение запаса? Тогда, когда время придет ( дата контроля запасов и выдачи заявки ), т.е. через 7 дней от начала расходования партии. - Когда придет новый заказ? Через 5 дней. Итого, от начала расходования запаса до момента получения новой партии пройдет 12 дней ( 7 + 5 ) = 12. - Какова величина запаса, при которой наступает плановая поставка новой партии? Эта величина определяется как разность между текущим запасом в точке контроля ( Qтек ) и запасом, потребленным за время ожидания заказа: ( Qтек – Sп х Т ). При этом текущий запас равен разности между Qмакс и запасом, израсходованным при работе до точки контроля ( 120 – 10 х 7 = 50 ). Следовательно, поставка новой партии происходит при достижении запасом значения 0 штук ( 50 – 10 х 5 = 0 ). -Каков буде максимальный запас при поступлении заказа? Как указывалось выше, размер партии заказа в каждом цикле рассчитывается исходя из стремления после получения очередной партии иметь первоначально определенный максимальный размер запаса. В этом случае определение системой размера партии заказа состоит из суммирования размеров запаса, потребленного до точки контроля ( Qмакс –Qтек ), и запаса, который будет израсходован за время ожидания поставки ( Т х Sп ): Qзаказа = Qмакс – Qтек + Т х Sп = 120 –5 0 + 5 х 10 = 120. В этом случае, как и требуется, запас при получении партии достигнет значения 120 штук ( 0 + 120 = 120 ). Следует отметить, что страховой запас « спас» систему от простоев при наступлении случая прогнозируемой задержки поставки. 2. .Восстановление системы при плановых параметрах ( Sп = 10; Т = 3 ) – цикл третий на рис.4. - Когда выдается заявка на пополнение запаса? Тогда, когда время придет ( дата контроля запасов и выдачи заявки ) – через 5 дней от начала расходования партии. - Когда придет новый заказ? Через 3 дня ( при отсутствии задержки ). Итого, от начала расходования запаса до момента получения новой партии пройдет 8 дней ( 5 + 3 ) = 8. - Какова величина запаса, при которой наступает плановая поставка новой партии? Эта величина определяется как разность между текущим запасом в точке контроля ( Qтек ) и запасом, потребленным за время ожидания заказа: ( Qтек – Sп х Т ). При этом текущий запас равен разности между Qмакс и запасом, израсходованным при работе до точки контроля ( 120 – 10 х 5 = 70 ). Следовательно, поставка новой партии происходит при достижении запасом значения 40 штук ( 70 – 10 х 3 = 40 ). -Каков буде максимальный запас при поступлении заказа? Как указывалось выше, размер партии заказа в каждом цикле рассчитывается исходя из стремления после получения очередной партии иметь первоначально определенный максимальный размер запаса. В этом случае определение системой размера партии заказа состоит из суммирования размеров запаса, потребленного до точки контроля ( Qмакс –Qтек ), и запаса, который будет израсходован за время ожидания поставки ( Т х Sп ): Qзаказа = Qмакс – Qтек + Т х Sп = 120 – 70 + 3 х 10 = 80. В этом случае, как и требуется, запас при получении партии достигнет значения 120 штук ( 40 + 80 = 120 ). 3. . Скачок потребления ( непрогнозируемый сбой ): Sп = 20; Т = 3 - четвертый цикл работы системы на рис. 4. - Когда выдается заявка на пополнение запаса? Тогда, когда время придет ( дата контроля запасов и выдачи заявки ) – через 7 дней от начала расходования партии. - Какова величина запаса, при которой наступает плановая поставка новой партии? Эта величина равна 0 штук, т.к. весь имеющийся запас в 120 штук расходуется за 6 дней : 120 : 20 = 6 Система будет простаивать 1 день до точки контроля и еще 3 дня ожидая получение заказа. Суммарное время простоя составит 4 дня. -Каков будет максимальный запас при поступлении заказа? В этом случае определение системой размера партии заказа состоит из суммирования размеров запаса, потребленного до точки контроля ( Qмакс –Qтек ), и запаса, который будет израсходован за время ожидания поставки ( Т х Sп ): Qзаказа = Qмакс – Qтек + Т х Sп = 120 – 0 + 3 х 0 = 120. В этом случае, как и требуется, запас при получении партии достигнет значения 120 штук ( 0 + 120 = 120 ). 4. Уменьшение потребления ( непрогнозируемый сбой ) Sп = 5; Т = 3 ( пятый цикл работы системы на рис. 4 ). - Когда выдается заявка на пополнение запаса? Тогда, когда время придет ( дата контроля запасов и выдачи заявки ) – через 7 дней от начала расходования партии. - Когда придет новый заказ? Через 3 дня ( при отсутствии задержки ). Итого, от начала расходования запаса до момента получения новой партии пройдет 10 дней ( 7 + 3 = 10 ). - Какова величина запаса, при которой наступает плановая поставка новой партии? Эта величина определяется как разность между текущим запасом в точке контроля ( Qтек ) и запасом, потребленным за время ожидания заказа: ( Qтек – Sп х Т ). При этом текущий запас равен разности между Qмакс и запасом, израсходованным при работе до точки контроля ( 120 – 5 х 7 = 85 ). Следовательно, поставка новой партии происходит при достижении запасом значения 70 штук ( 85 – 5 х 3 = 70 ). -Каков буде максимальный запас при поступлении заказа? В этом случае определение системой размера партии заказа состоит из суммирования размеров запаса, потребленного до точки контроля ( Qмакс –Qтек ), и запаса, который будет израсходован за время ожидания поставки ( Т х Sп ): Qзаказа = Qмакс – Qтек + Т х Sп = 120 – 85 + 3 х 5 = 50. В этом случае, как и требуется, запас при получении партии достигнет значения 120 штук ( 70 + 50 = 120 ). Сравнение основных систем управления запасами Можно предположить идеальную, сугубо теоретическую ситуацию, в которой исполнение заказа происходит мгновенно (другими словами, время поставки равно нулю). Тогда заказ можно производить в момент, когда запасы материальных ресурсов на складе равны нулю. При постоянной скорости потребления обе рассмотренные системы управления запасами (с фиксированным размером заказа и с фиксированным интервалом времени между заказами) становятся одинаковыми, так как заказы будут производиться через равные интервалы времени, а размеры заказов всегда будут равны друг другу. Гарантийные запасы каждой из двух систем сведутся к нулю. Такая ситуация проиллюстрирована на рис.5. 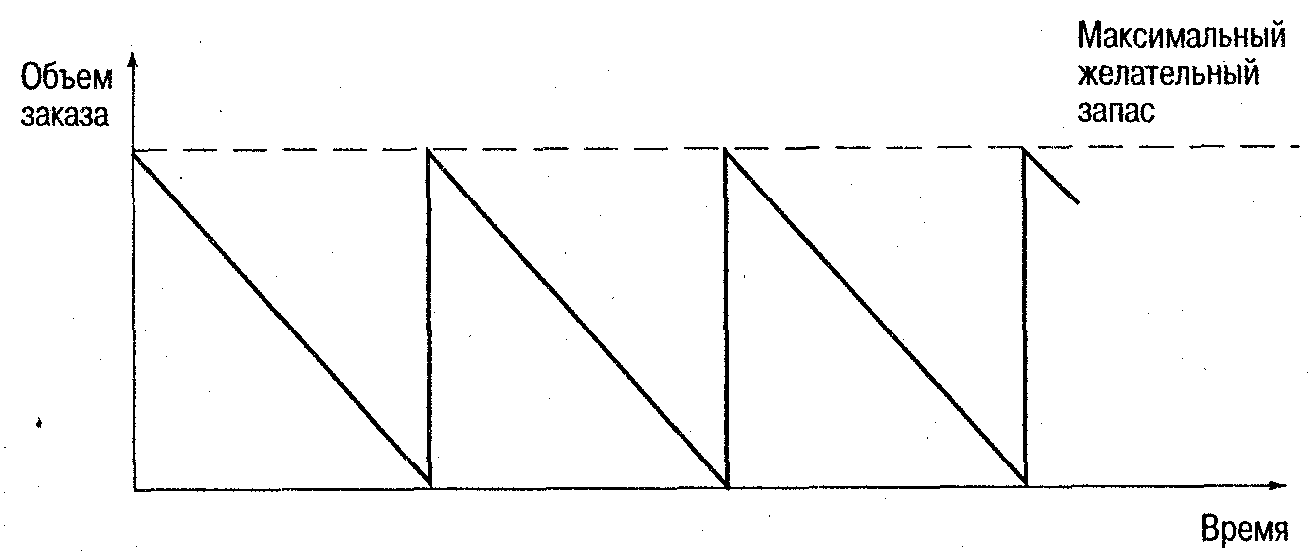 Рис. 5. График движения запасов в основных системах управления запасами при мгновенном исполнении заказа Сравнение рассмотренных систем управления запасами приводит к выводу о наличии у них взаимных недостатков и преимуществ. Система с фиксированным размером заказа требует непрерывного учета текущего запаса на складе. Напротив, система с фиксированным интервалом времени между заказами требует лишь периодического контроля количества запаса. Необходимость постоянного учета запаса в системе с фиксированным размером заказа можно рассматривать как основной ее недостаток. Напротив, отсутствие постоянного контроля за текущим запасом в системе с фиксированным интервалом времени между заказами является ее основным преимуществом перед первой системой. Следствием преимущества системы с фиксированным интервалом времени между заказами является то, что в системе с фиксированным размером заказа максимальный желательный запас всегда имеет меньший размер, чем в первой системе. Это приводит к экономии на затратах по содержанию запасов на складе за счет сокращения площадей, занимаемых запасами, что, в свою очередь, составляет преимущество системы с фиксированным размером заказа перед системой с фиксированным интервалом времени между заказами. Преимущества и недостатки рассмотренных систем управления запасами сведены в табл.1. Таблица 1 Сравнение основных систем управления запасами
Прочие системы управления запасами Разобранные выше основные системы управления запасами базируются на фиксации одного из двух возможных параметров — размера заказа или интервала времени между заказами. В условиях отсутствия отклонений от запланированных показателей и равномерного потребления запасов такой подход является вполне достаточным. Однако на практике чаще встречаются иные, более сложные ситуации Различное сочетание звеньев основных систем управления запасами, а также добавление принципиально новых идей в алгоритм работы системы приводит к возможности формирования, по сути дела, огромного числа систем управления запасами, отвечающих самым разнообразным требованиям., Остановимся на двух наиболее распространенных прочих системах: 1) системе с установленной периодичностью пополнения запасов до постоянного уровня; 2) системе «минимум—максимум». Система с установленной периодичностью пополнения запасов до постоянного уровня Эта система проектируется тогда, когда прогнозируется возможность временного увеличения потребления и необходимо предотвратить возникновение вероятных простоев. Алгоритм работы данной системы следующий: - при потреблении плановом или меньшем должен реализовываться принцип управления системы с фиксированным интервалом контроля, т.е выдача заявки на пополнение запаса происходит при достижении определенного времени ( даты ); - при скачке потребления должен реализовываться принцип управления системы с фиксированным размером заказа, т.е. заявка выдается при достижении порогового уровня. Другими словами, в каждом цикле реализуется тот принцип ( «временной» или «запасный» ), до которого успевает дойти система. Некоторые особенности проектирования и функционирования системы рассмотрим с использованием рис.6. Исходные данные : • оптимальный размер заказа, шт. ……….. ОРЗ = 100 • темп потребления, шт/день. ……………… Sп = 10 • время поставки, дни ………………………. Т = 3 • возможная задержка поставки, дни ( прогнозируемый сбой )………. …………… Тз = 2 • возможный скачок потребления, шт/день ( прогнозируемый сбой )…………………………….Sпс = 15 Проектирование системы для работы с плановым и меньшим потреблением аналогично рассмотренному выше примеру ( рис. 4 ). Это знакомая нам система с фиксированным интервалом контроля – первый цикл на рис.6. Но для предотвращения простоев при скачке потребления ( прогнозируемом ) необходимо организовать и контроль по запасам с помощью порогового уровня. В этом случае заявка должна выдаваться раньше достижения точки контроля по времени, а имеющийся пороговый запас обеспечит работу системы без простоев за время выполнения заказа. Следовательно, пороговый уровень равен 45 штукам: Qпор = Sпс х Т = 15 х 3 =45 Во втором цикле работы ( рис.6 ) рассмотрено поведение системы при возникновении прогнозируемого скачка. - Когда выдается заявка на пополнение запаса? Когда будет достигнута точка контроля или пороговый уровень; - Через сколько дней это произойдет? В этом случае, не дойдя 2 дня до точки контроля по времени, система раньше достигает порогового уровня ( через 5 )дней : (120 – 45 ) : 15 = 5 - Когда придет новый заказ? Через 3 дня ( при отсутствии задержки ). Итого, от начала расходования запаса до момента получения новой партии пройдет 8 дней: ( 5 + 3 ) = 8 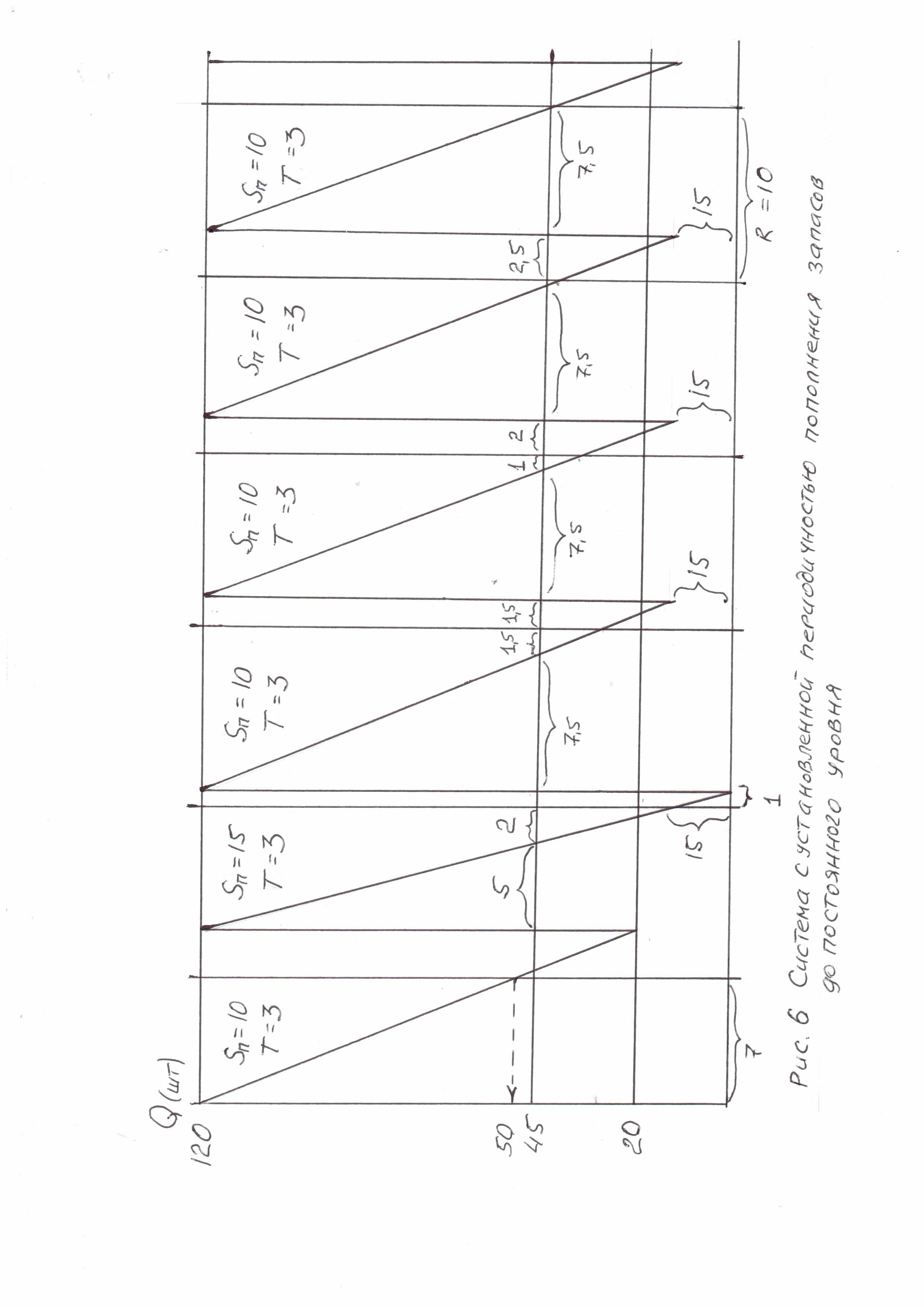 - Какова величина запаса, при которой наступает плановая поставка новой партии? Заявка выдается при достижении запасом уровня 45 штук, который за время выполнения заявки потребляется полностью : ( Т х Sп = 3 х 15 = 45 ). -Каков будет максимальный запас при поступлении заказа? Он будет равен 120 штукам: ( Qтек + ОРЗ ) = 0 + 120 = 120 Система без простоев отреагировала на прогнозируемый скачок потребления. Читатели могут самостоятельно убедиться в том, что при отсутствии порогово- го уровня в 45 штук, выдав заявку в точке контроля по времени, система простаивала бы без запаса в течении 2 дней. Но следует сказать, что для рассматриваемой системы существует определен- ный максимум скачка потребления, который может быть нейтрализован без на- рушения алгоритма ( методологии ) работы. Это объясняется тем, что порого- вый уровень не может быть больше значения Qтек при плановом потреблении ( больше 50 штук для наших условий ). В противном случае, даже при плановом потреблении момент достижения системой порогового уровня будет наступать раньше соответствующей даты контроля, что приведет в итоге к излишне час- тым случаям выдачи заказов и несменяемости определенной части страхового запаса. Из сказанного следует, что можно аналитически определить предельное значе- ние скачка потребления, при котором может быть реализована рассматриваемая система управления запасами : Sп пред = Qтек : Т = 50 : 3 = 16,7 Продолжая анализировать поведение системы на рис.6. необходимо отметить, что после скачка потребления «к норме» она приходит только через 4 цикла работы. Напомним, что «нормой» считается выдача заявки на пополнение запаса при плановом потреблении при достижении очередной даты контроля. В первом цикле после скачка потребления ( в третьем цикле с начала графика на Рис.6 ) запас снижается до порогового за 7.5 дней : ( 120 – 45 ) : 10 = 7.5 т.е. на 1.5 дня раньше наступления точки контроля по времени. При этом текущий запас, при котором пополняется запас новой партией, будет равен 15 штукам: Qпор – ( Т х Sп ) = 45 – 3 х 10 =15 Во втором цикле достижение порогового уровня происходит на 1 день раньше наступления даты контроля, а в третьем цикле на 0,5 дня. И только в четвертом цикле ( в шестом цикле с начала графика ) точки выдачи заказа «по запасам» и «по времени» совпадут, что приведет к стабилизации системы в следующем цикле ее работы. |
