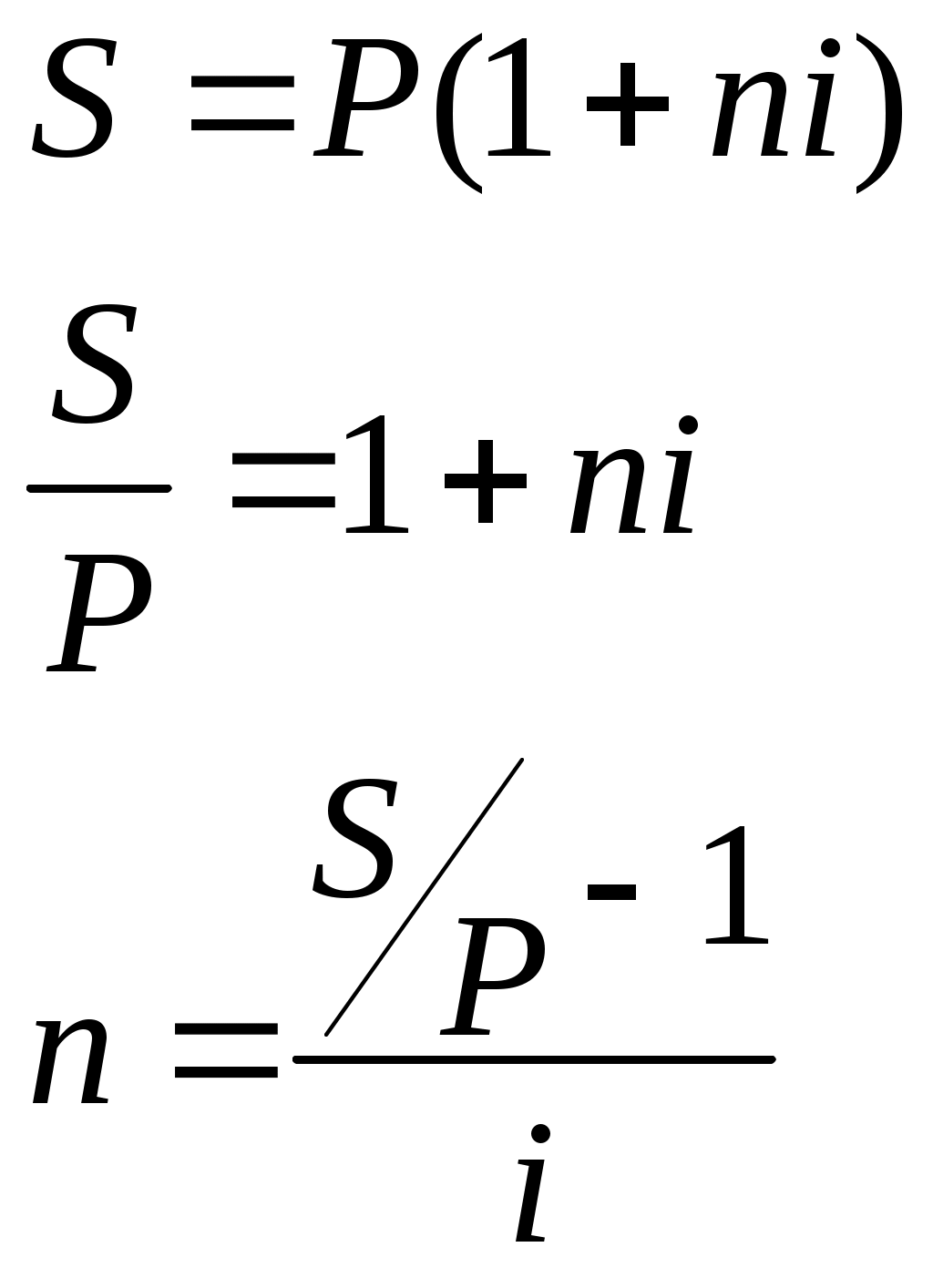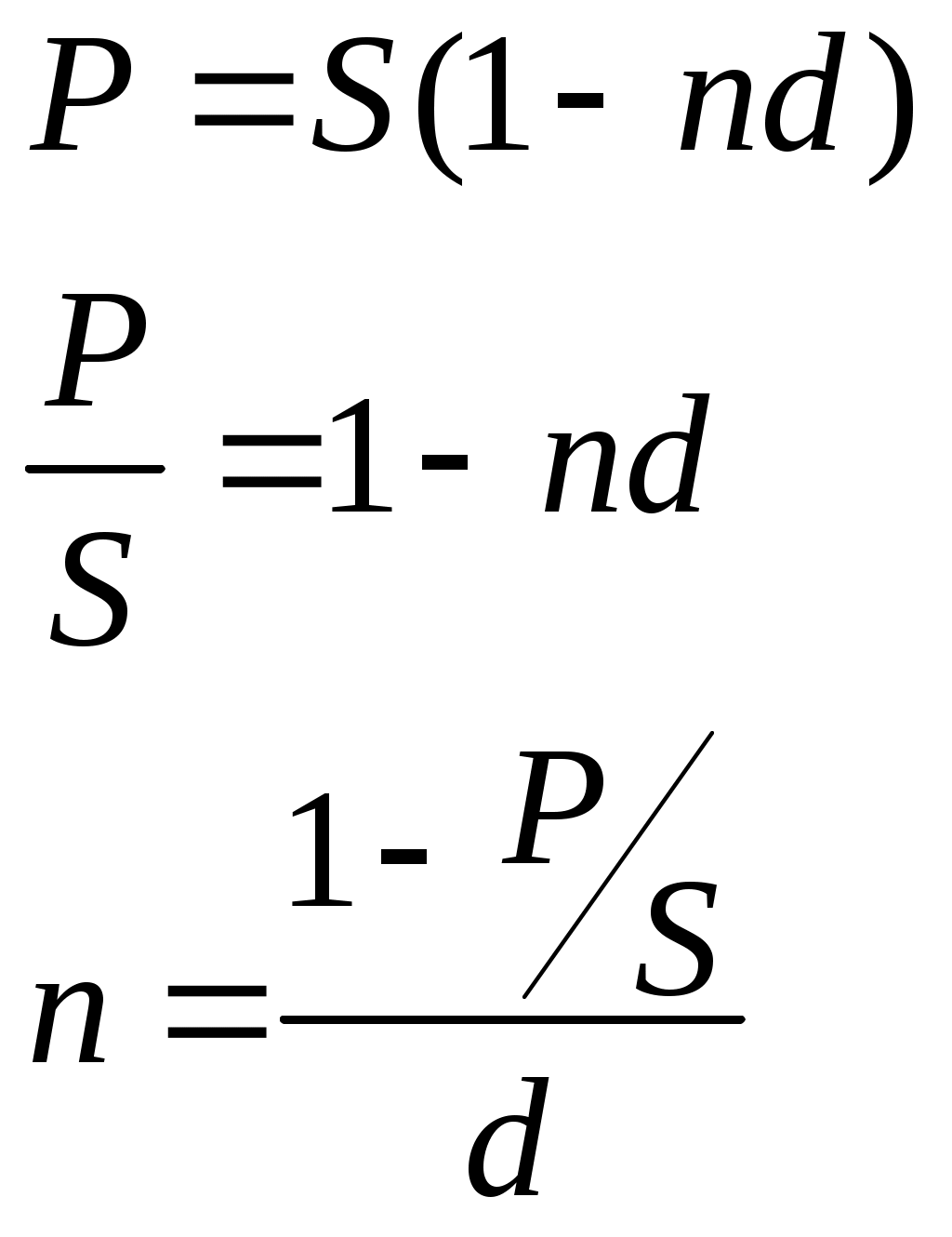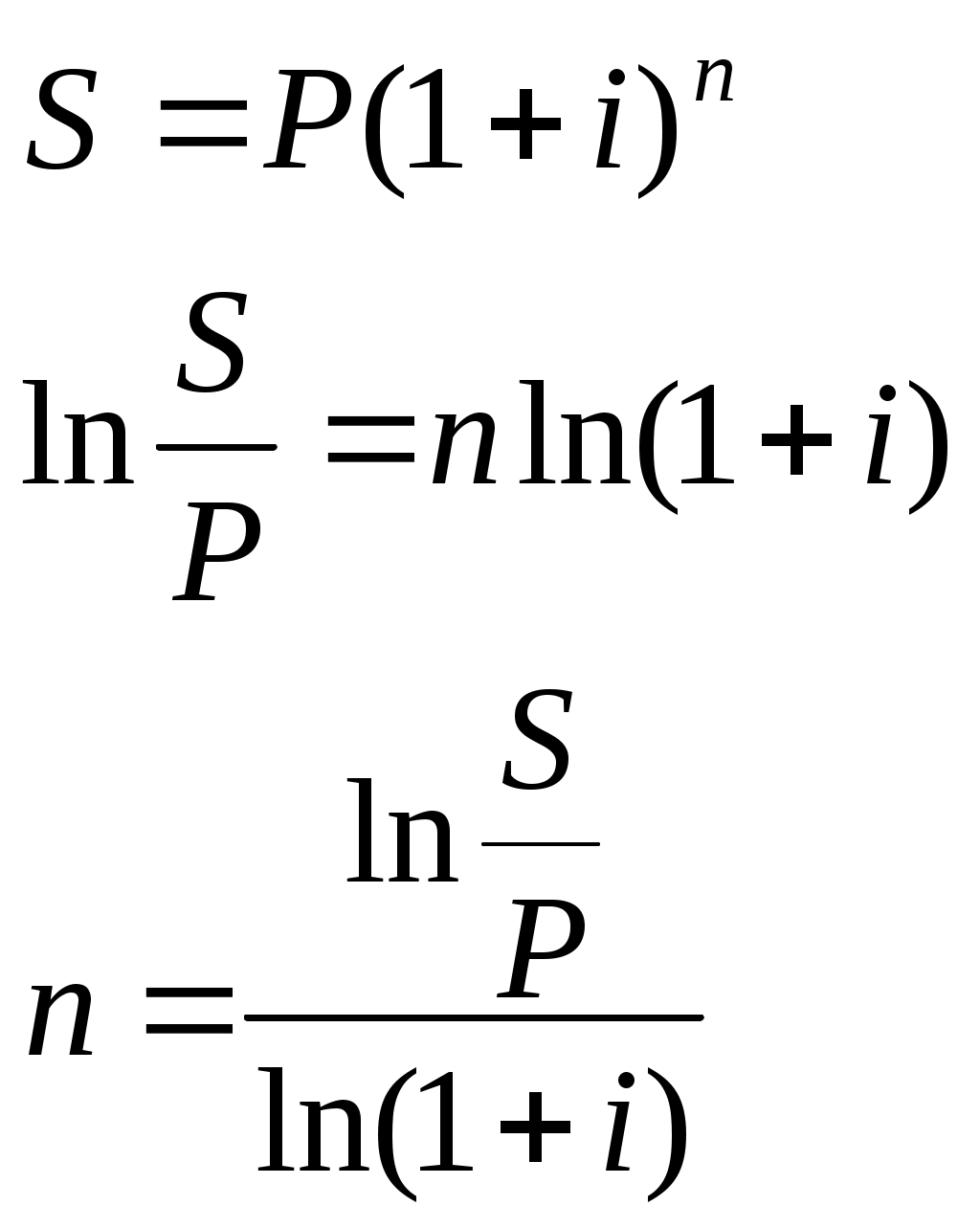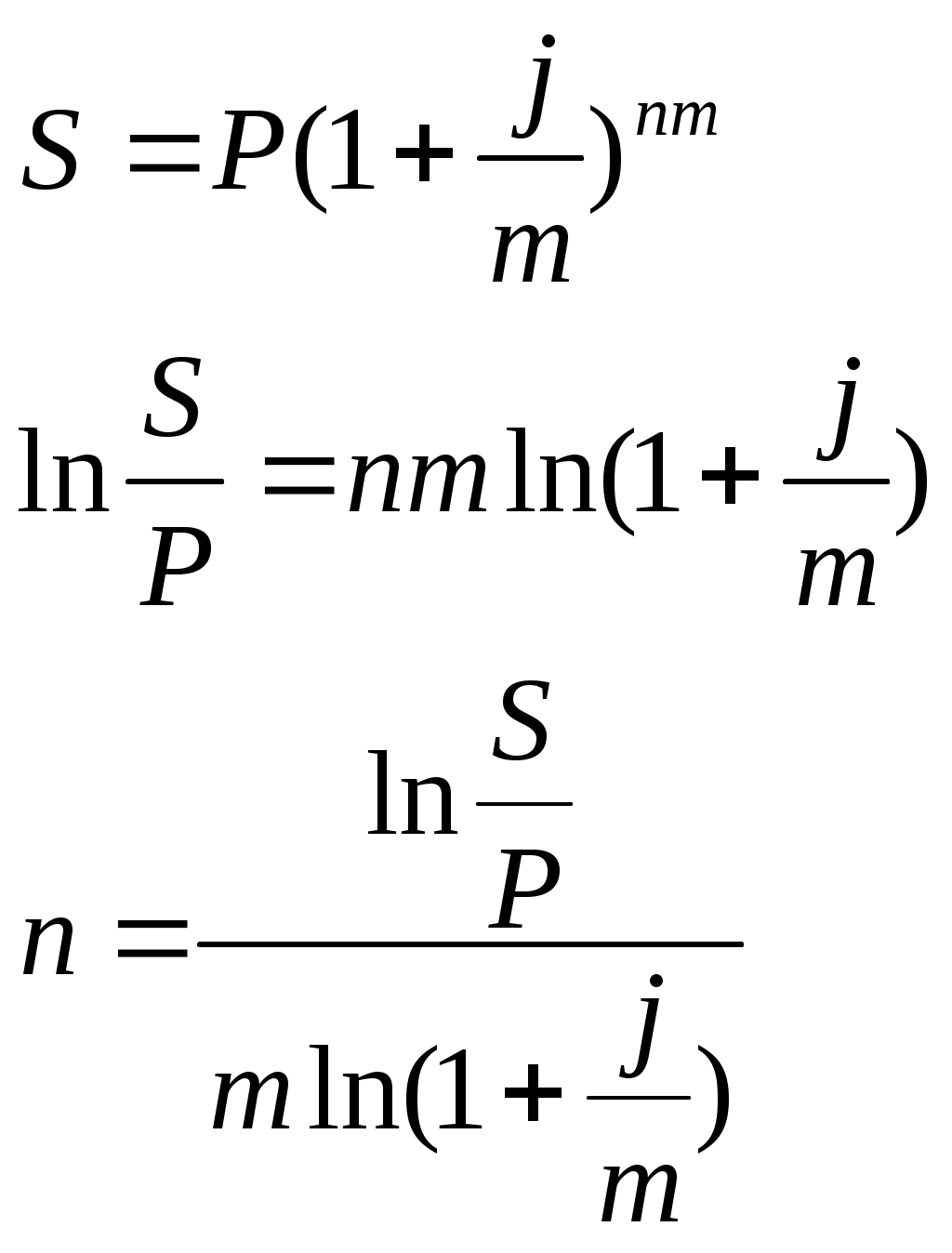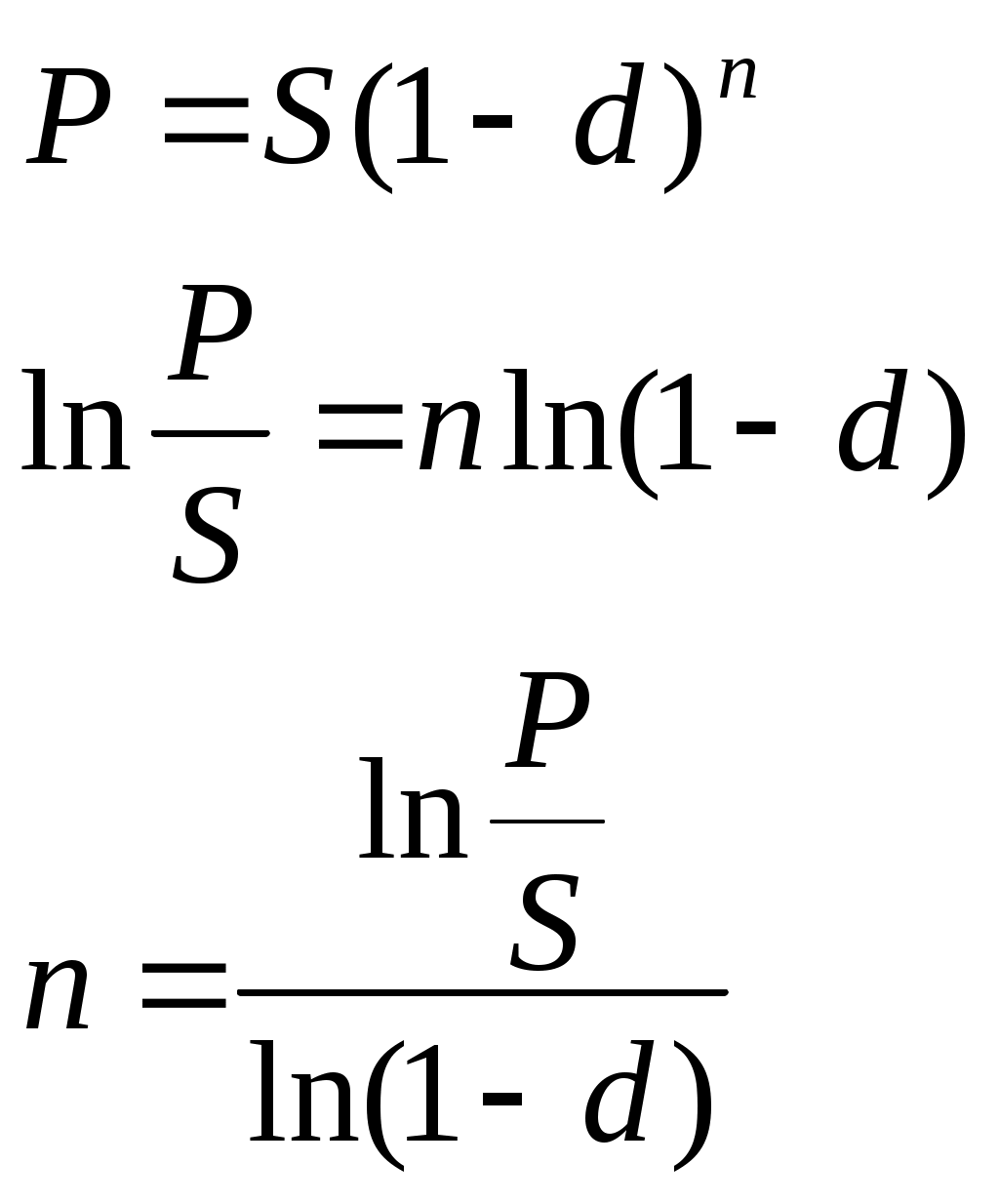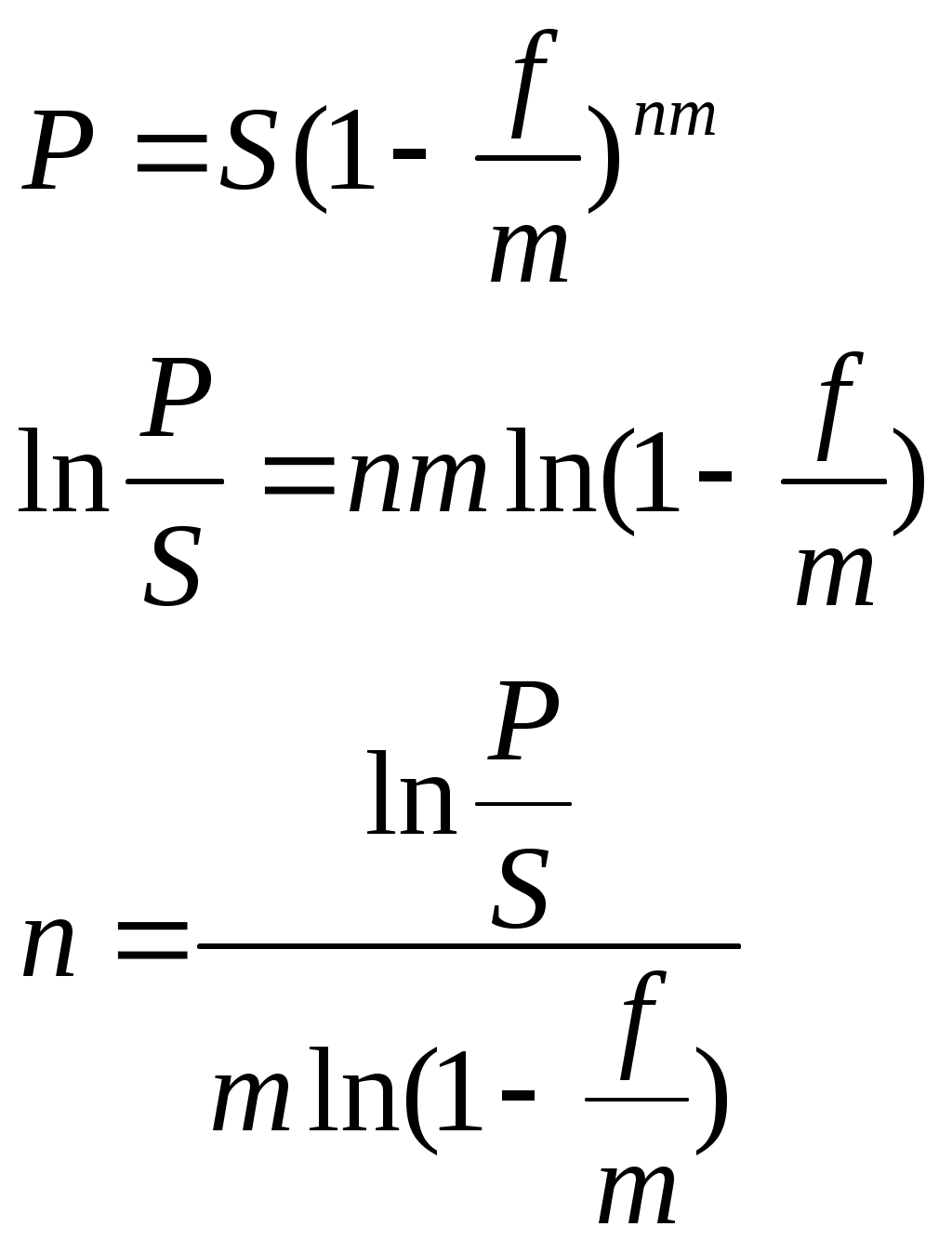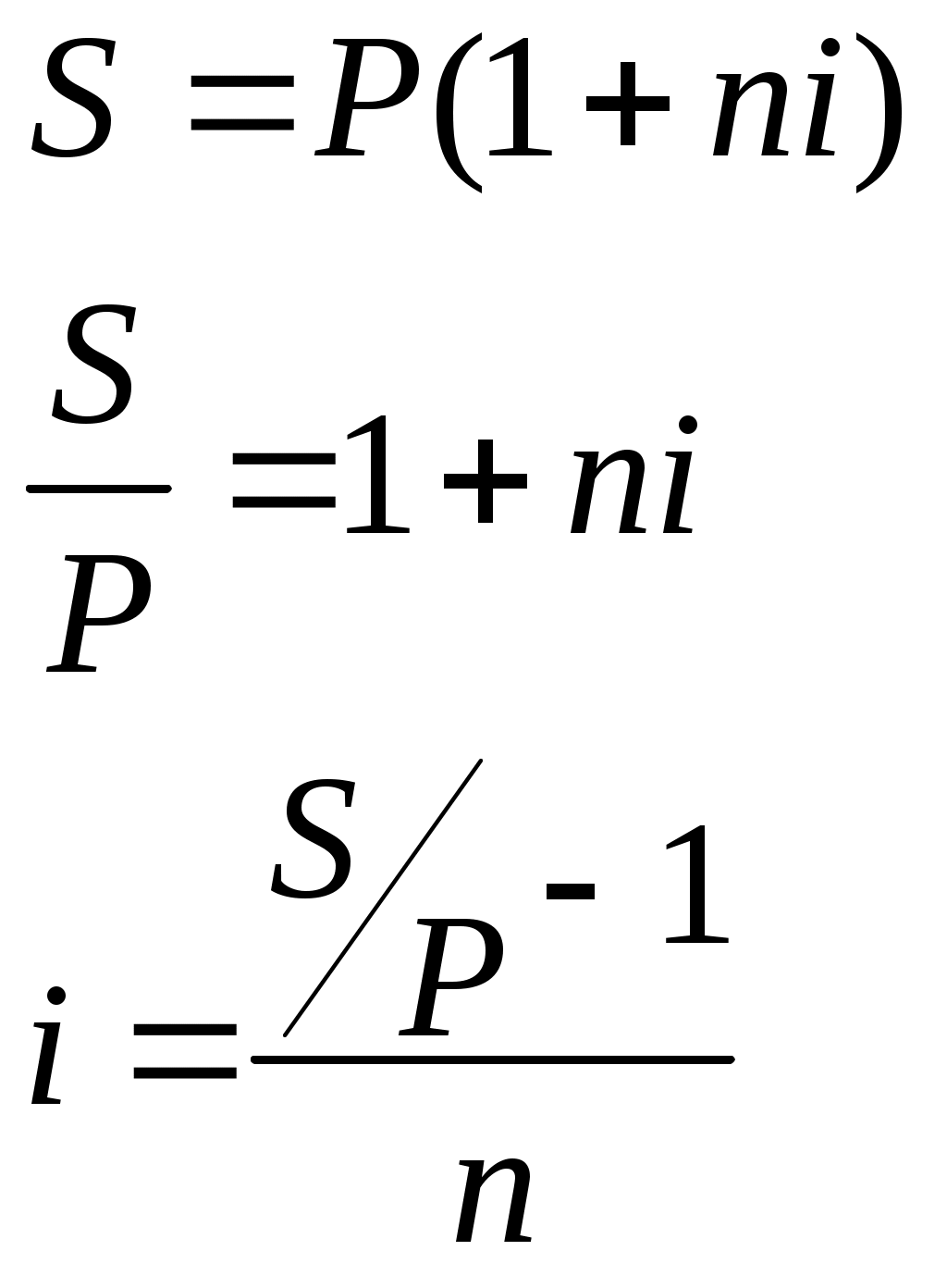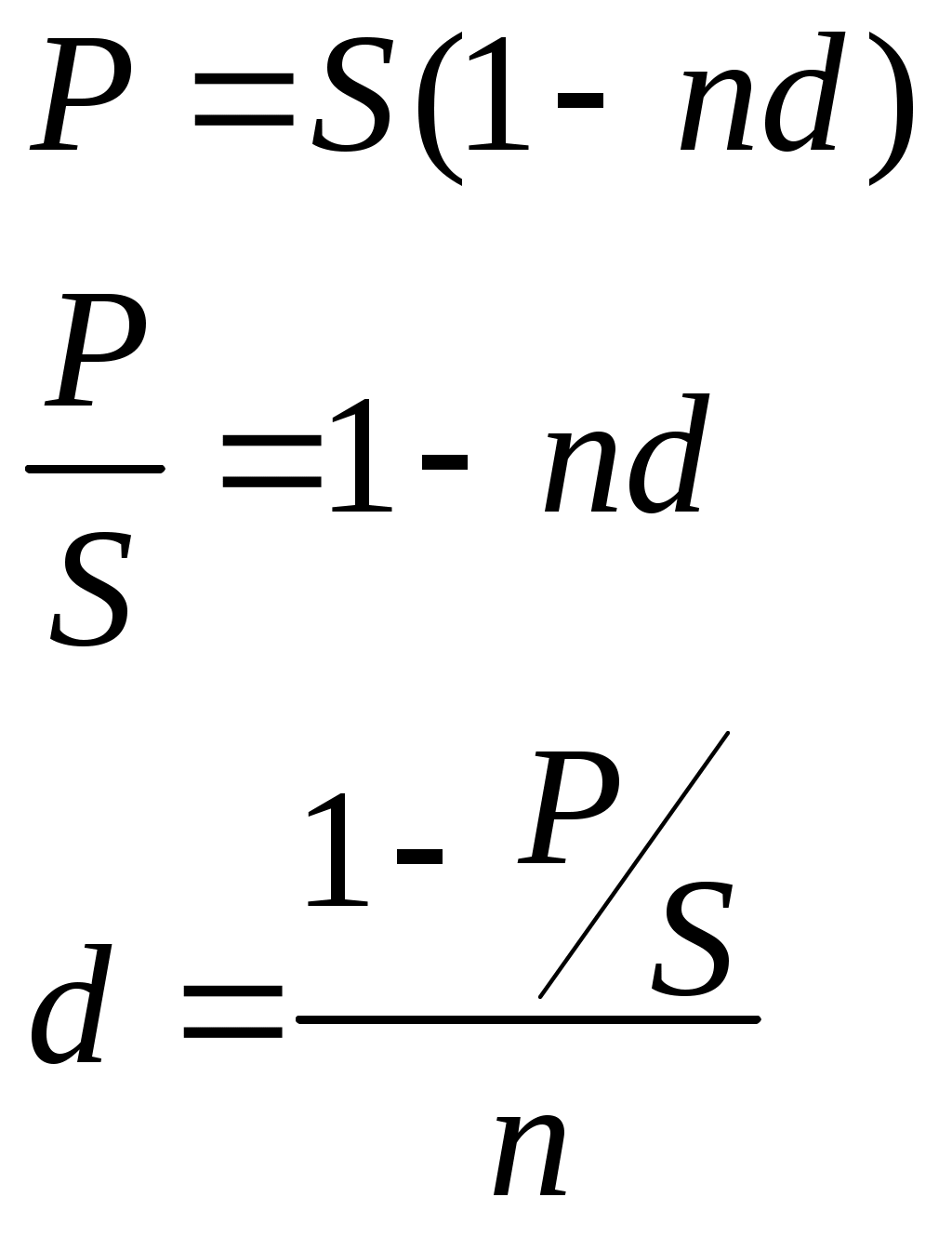Методические рекомендации по выполнению практических работ по учебной дисциплине
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
Контрольные вопросы Уровень и индекс инфляции. Инфляционная премия. Модели расчета процентных ставок, учитывающих инфляцию. Практическая работа №5 Исследование сравнения финансово-коммерческих операций. Цель: научиться проводить сравнение финансово-коммерческих операций. Теоретические обоснования Для определения срока или ставки финансовой операции необходимо, из уже знакомых формул наращения и дисконтирования по процентным и учетным ставкам, выразить период или ставку.
Практические задания Задача 1. Построить таблицы и графики ежегодного изменения коэффициентов наращения для различных ставок сложных процентов 5%, 10%, 15%, 20%, за период 8 лет. Задача 2. Построить таблицы и графики ежегодного изменения коэффициентов наращения для различных ставок сложных процентов 12%, 15%, 18%, 20%, за период 6 лет. Задача 3 Какова эффективная ставка процентов, если номинальная ставка равна 35 % при помесячном начислении процентов. Задача 4. Определить значение учетной ставки банка, эквивалентной ставке простых процентов 35 % годовых. Задача 5. Вексель учтен в банке по номинальной учетной ставке 20 % годовых с ежемесячным дисконтированием. Определить значение эффективной годовой ставки процентов. Задача 6. Определить значение учетной ставки банка, эквивалентной ставке простых процентов 30 % годовых, сроком 2 года. Задача 7. Определить значение учетной ставки банка, эквивалентной ставке сложных процентов 20 % годовых. Задача 8. Сумма в размере 4000 тыс. р. возрастает до 5000 тыс. р. при ставке сложных процентов 5% годовых. Определить срок выполнения такой финансовой операции. Задача 9. Срок платежа по векселю составляет 2 года. Эффективность операции учета в банке должна составлять 15 % годовых по простой ставки процентов. Определить эквивалентное значение учетной ставки. Задача 10. Вексель учтен в банке по учетной ставке 30 % годовых за полгода до срока его погашения. Определить значение эквивалентной простотой годовой ставки процентов. Задача 11. При учете векселя на сумму 500000 р., до срока оплаты которого осталось 60 дней, банк выплатил предъявителю 460000 р. Определить величину простой учетной ставки банка и эквивалентной ей процентной ставки. Задача 12. Определить эффективную учетную ставку и сумму дисконта, если известно, что финансовый инструмент на сумму 5 млн. р., срок платежа по которому наступает через пять лет, продан с дисконтом при поквартальном дисконтировании по номинальной учетной ставке 15 %. Задача 13. Сумма в размере 400 р. возрастает до 4500 р. при ставке сложных процентов 15% годовых. Определить срок выполнения такой финансовой операции, а также доходность операции в виде сложной учетной ставки. Задача 14. Определить доходность операции, в виде сложной процентной ставки, если за два года первоначальная сумма возросла в 2 раза. Начисление процентов раз в год. Определить эквивалентную ставку. Контрольные вопросы Виды финансово - коммерческих операций. Уравнения эквивалентности. Эффективная ставка процентов. Номинальная и эффективная ставки процентов. Потоки платежей и их характеристики. Практическая работа №6 Модели операций с акциями и облигациями. Цель: научиться проводить финансово-коммерческие операции с ценными бумагами Практические задания Задача 1. Курс акций на 11 июля составил: покупка 7300 руб., продажа 8000 руб., а на 28 сентября соответственно покупка 11750 руб., продажа 14750руб. Определить доход, полученный от покупки 100 акций 11 июля и их последующей продажи 28 сентября, а так же доходность операции купли-продажи в виде эффективной ставки простых процентов. Задача 2. Облигации, выпущенные банком с купонной ставкой 8,5%, продаются на первичном рынке по номиналу. Двумя годами раньше банк уже выпускал облигации, но с купонной ставкой 8%. Определить будет ли её текущая рыночная цена выше или ниже номинала. Задача 3. Акции номиналом 1000 руб. были куплены по цене 2,5 тыс. руб. за полгода для выплаты дивидендов. Дивиденд по акциям за год был объявлен в размере 200% годовых. После объявления о выплате дивидендов курс акции составил 2,8 тыс. руб. Определить текущую доходность в виде эффективной ставки процентов. Задача 4. Операция, связанная с покупкой и последующей продажей облигаций, должна принести через 3 года прибыль в 100 000 руб. Определите современную ценность этой суммы по сложной годовой учетной ставке d=30%. Задача 5. Облигация куплена по курсу 80 и будет погашена через 5 лет после покупки. Ежегодные проценты ( купонные платежи) выплачиваются в конце года по ставке 7% годовых. Определить доходность этой покупки по эффективной ставке процентов. Задача 6. Акция номинальной стоимостью 500 руб. приобретена по курсу 2500 руб. Дивиденд по акции составляет 200 руб. Определить конечную годовую доходность. Задача 6. Переводный вексель (тратта) выдан на 100 000 руб. с уплатой 12 ноября того же года. Владелец векселя учёл его в банке досрочно – 12 сентября по простой учетной ставке 10%. Определите сумму, полученную владельцем векселя в банке, если число дней в году принять равным K=360. Задача 7. Облигации номиналом 100 тыс. руб. и сроком обращения 180 дней были куплены в момент их выпуска по курсу 66,5 и проданы через 30 дней по курсу 88. Определить доходность купленных облигаций к погашению и текущую доходность купленных облигаций к погашению и текущую доходность купленных облигаций к аукциону в результате продаже, для расчетного количества дней в году 360. Задача 8. Курс акций на 23 июля составил: покупка 15300 руб., продажа 2000 руб., а на 2 сентября соответственно покупка 19750 руб., продажа 20750руб. Определить доход, полученный от покупки 100 акций 23 июля и их последующей продажи 2 сентября, а так же доходность операции купли-продажи в виде эффективной ставки простых процентов. Контрольные вопросы Виды операций с ценными бумагами. Модели расчета операций с облигациями. Модели расчета операций с акциями. Оценка доходов и доходности операции с ценными бумагами. Практические задания Практическая работа №7 Нахождение приближающейся функции в виде квадратного трехчлена. Цель: овладение практическими навыками построения эмпирических формул методом наименьших квадратов для параболы. Практические задания Указание по выполнению работы. Задания выполняются с помощью математического процессора MathCad и графической программы Advanced Grapher. Теоретические упражнения. Постановка задачи метода наименьших квадратов; метод нахождения параметров приближающей функции в общем виде y = f(x, a, b, c); нахождение приближающей функции в виде линейной функции и квадратного трехчлена; нахождение приближающей функции в виде других элементарных функций: степенной, показательной, дробно-линейной, логарифмической, гиперболы дробно-рациональной. Варианты к заданиям:
Задания: По заданной таблице значений xi и yi составьте точечный график и методом наименьших квадратов найдите и уточните приближающую функцию в виде линейной функции. Постройте график линейной функции с учетом поправки. Для найденной функции вычислите сумму квадратов уклонений. По заданной таблице значений xi и yi составьте точечный график и методом наименьших квадратов найдите и уточните приближающую функцию в виде функции квадратного трехчлена. Постройте график функции квадратного трехчлена с учетом поправки. Для найденной функции вычислите сумму квадратов уклонений. Контрольные вопросы. 1. В чем сущность метода наименьших квадратов? 2. Какие функции MathCAD реализует линейную аппроксимацию методом наименьших квадратов? 3. Какой диапазон изменения значений коэффициента корреляции? 4. Что такое эмпирическая формула и как ее подобрать? 5. Перечислите типовые функции регрессии. Практическая работа №8 Показательная функция. Цель: Овладение практическими навыками построения эмпирических формул методом наименьших квадратов для экспоненты. Теоретические обоснования Показательная зависимость имеет вид Во всех случаях Если найденная на опыте зависимость  Рисунок 2 График показательной функции Найдем коэффициенты Прологарифмируем равенство (6) : приняв обозначения Таким образом приближающая показательная функция нехитрыми преобразованиями сведена к линейной, следовательно, для определения коэффициентов 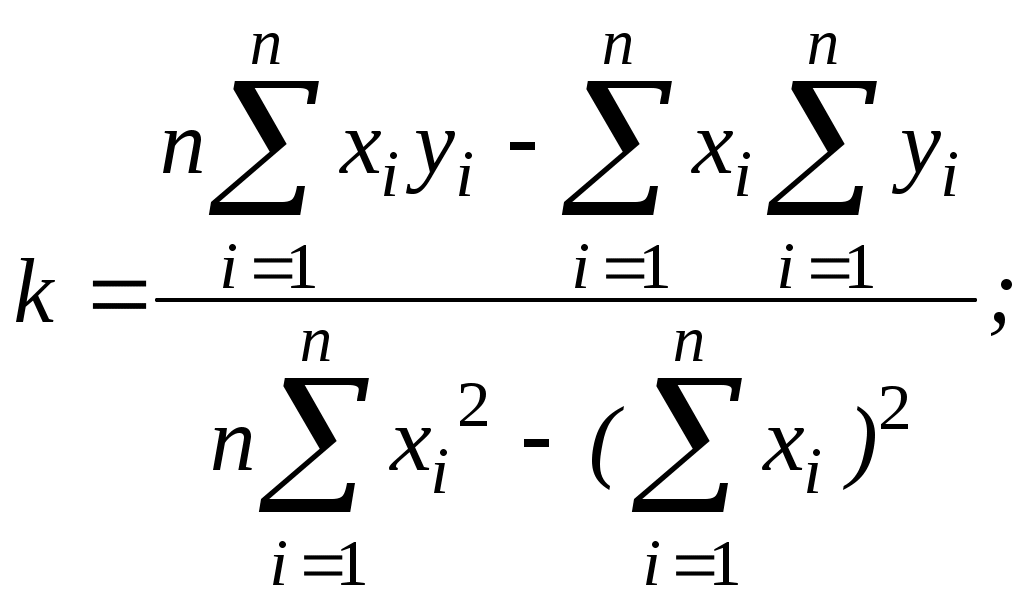 (9) (9)Итак, для нахождения приближающей функции в виде (6) нужно прологарифмировать значения функции в исходной таблице 1 и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы 3 приближающую функцию вида (8). Таблица 1 Таблица 3
Окончательно получаем: 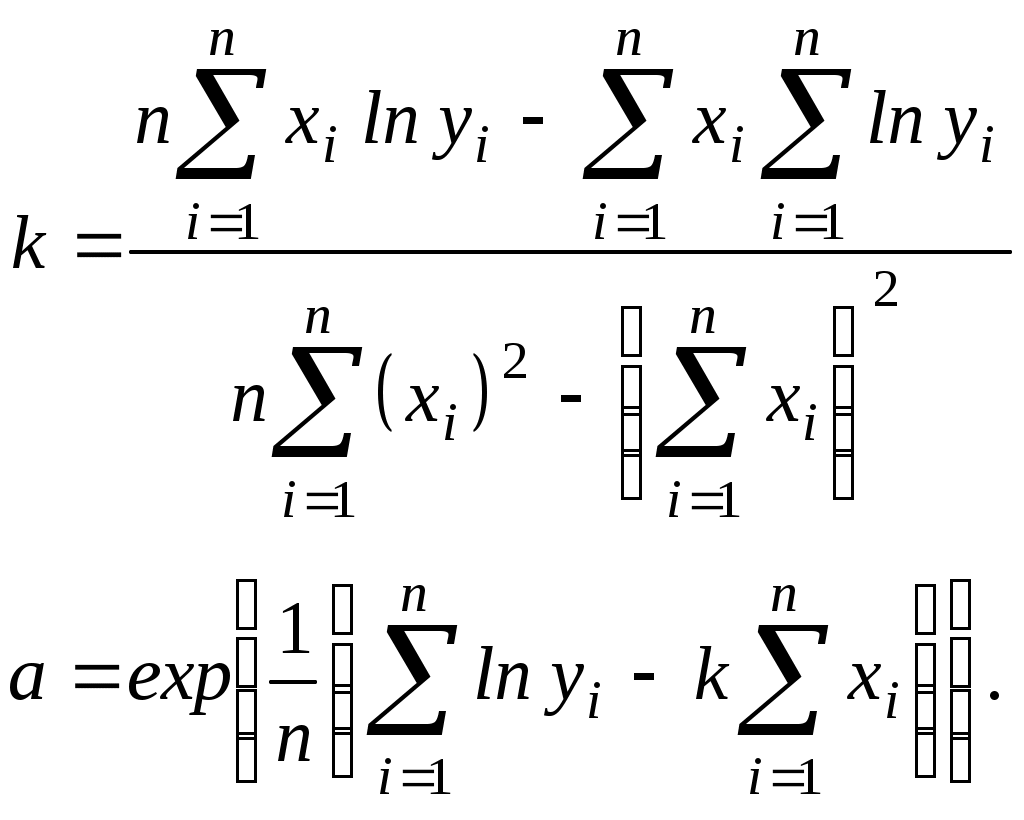 (9) (9) Рисунок 3 – График логарифмической функции Замечание: формулам соответствуют кривые, изображенные на рисунках 1 и 2, сдвинутые вверх или вниз на величину 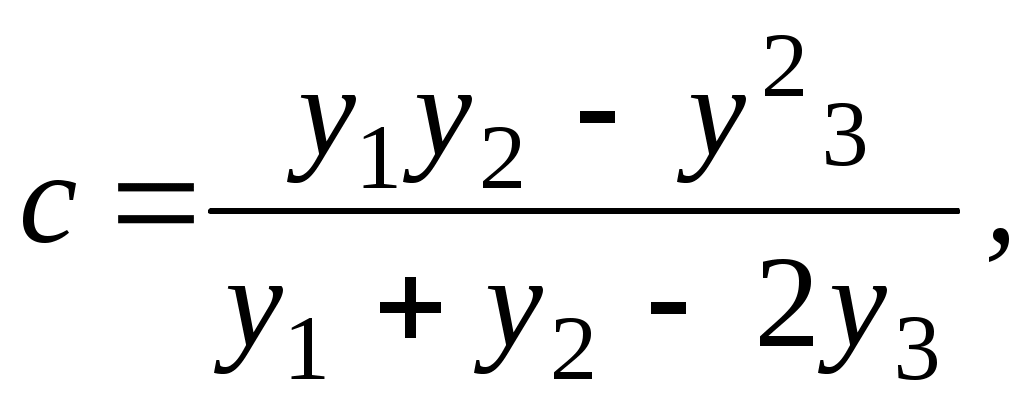 где | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||