Методические рекомендации по выполнению практических работ по учебной дисциплине
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего образования «Курский государственный университет» Колледж коммерции, технологий и сервиса Методические рекомендации по выполнению практических работ по учебной дисциплине Основы исследовательской деятельности для студентов четвертого курса специальности 09.02.05 Прикладная информатика (по отраслям)  Составитель: к.т. н., Ефимцева И. Б.- преподаватель колледжа коммерции, технологий и сервиса ФГБОУ ВО «Курский государственный университет» Курск, 2016 ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ
Порядок выполнения отчета по практической работе 1. Ознакомиться с теоретическим материалом по практической работе. 2. Выполнить предложенное задание согласно варианту по списку группы. 3. Продемонстрировать результаты выполнения предложенных заданий преподавателю. 4. Составить по практической работе отчет. 5. Ответить на контрольные вопросы. Практическая работа №1 Простые проценты. Цель: разобрать понятие простых процентов, сущность операции дисконтирования, понятие учетной ставки, научиться работать с формулами. Теоретические обоснования При начислении простых процентов по ставке i за базу берется первоначальная сумма долга Р. Наращенная сумма S растет линейно от времени. Под процентными деньгами или процентами I в финансовых расчетах понимают абсолютную величину дохода от предоставления денег в долг в любой форме: в виде выдачи денежной ссуды, продажи в кредит, помещении денег на сберегательный счет, учет векселя, покупка сберегательного сертификата или облигаций и т.д. В какой бы форме не выступали проценты, это всегда конкретное проявление такой экономической категории, как ссудный процент. При заключении финансового или кредитного соглашения стороны (кредитор и заемщик) договариваются о размере процентной ставки - отношения суммы процентных денег, выплачиваемых за фиксированный отрезок времени к величине ссуды. Продолжительность времени, к которой относится процентная ставка, называют периодом начисления. Ставка измеряется в процентах и задается величиной за год в виде десятичной или натуральной дроби. Начисление процентов, в основном, производится дискретно, т.е. в отдельные (обычно равноотстоящие) моменты времени (дискретные проценты). В качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуют ежедневное начисление, а в ряде случаев удобно применять непрерывные проценты. Процентные ставки, указываемые в контрактах, могут быть постоянными или переменными («плавающими»). Плавающие ставки часто применяются во внешнеэкономических операциях. Ставка процентов обычно устанавливается в расчете за год, поэтому при продолжительности ссуды менее года необходимо выяснить, какая часть процента уплачивается кредитору. Для этого величину n (срок ссуды) выражают в виде дроби: n = t/K, где: n - срок ссуды (измеренный в долях года), K - число дней в году (временная база), t - срок операции (ссуды) в днях. Существует несколько вариантов расчета процентов, различающихся выбором временной базы K и способом измерения срока пользования ссудой. Часто за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней в каждом). В этом случае говорят, что вычисляют обыкновенный или коммерческий процент. В отличие от него точный процент получают, когда за базу берут действительное число дней в году: 365 или 366. Определение числа дней пользования ссудой также может быть точным или приближенным. В первом случае вычисляют фактическое число дней между двумя датами, во втором - продолжительность ссуды определяется числом месяцев и дней ссуды, приближенно считая все месяцы равными, содержащими по 30 дней. В обоих случаях счет дней начинается со следующего дня после открытия операции. Подсчет точного числа дней между двумя датами можно осуществить на компьютере, взяв разность этих дат, или с помощью специальной таблицы, в которой представлены порядковые номера дат в году. Комбинируя различные варианты временной базы и методов подсчета дней ссуды, получаем три варианта расчета процентов, применяемые в практике финансовых вычислений: (1) точные проценты с точным числом дней ссуды (365/365) - британский; (2) обыкновенные проценты с точным числом дней ссуды (365/360) -французский; (3) обыкновенные проценты с приближенным числом дней ссуды (360/360) - германский. Вариант расчета с точными процентами и приближенным измерением времени ссуды не применяется. Проценты либо выплачиваются кредитору по мере их начисления, либо присоединяются к сумме долга. Процесс увеличения денег в связи с присоединением процентов к сумме долга называют наращением или ростом первоначальной суммы. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды (простые проценты) или к сумме с начисленными в предыдущем периоде процентами (сложные проценты). Таблица 1Простые проценты, наращение
Когда по заданной сумме, соответствующей концу финансовой операции, требуется найти исходную сумму, получаемую заемщиком, решается задача, обратная наращению. Такая операция называется дисконтированием конечной суммы долга. Основные формулы дисконтирования, необходимые для решения задач по разделу 1 (простые проценты), приведены в таблице 2. Таблица 2 Простые проценты, дисконтирование
Операции наращения и дисконтирования по своей сути противоположны, но ставка наращения и учетная ставка могут использоваться для решения обеих задач. В этом случае, в зависимости от применяемой ставки, можно различать прямую и обратную задачи (таблица 3).Таблица 3 Прямая и обратная задачи
Практические задания Задача 1. Вкладчик положил в банк под 15% годовых три тысячи рублей, какая сумма будет на счете вкладчика а) через три месяца; б) через год; в) через три с половиной года? Задача 2. Годовая ставка простых процентов составляет 14%. Через сколько лет вложенная сумма удвоится? Задача 3. Переводный вексель (тратта) выдан на сумму 100 000 руб. с уплатой 15.10. Владелец векселя учёл его в банке раньше 10.09 по учетной ставке 20%. Определить получаемую при учёте сумму и дисконт. Задача 4. Какую сумму необходимо положить в банк при условии 15% годовых так, чтобы накопить 50 000 руб. через 6 месяцев; через год; через 2 года 8 месяцев. Задача 5. Покупатель купил в кредит костюм стоимостью 9000 руб. и уплатил в момент приобретения 2000 руб., а на остальную сумму получил кредит на 6 месяцев под 12% годовых на условии гашения долга равными ежемесячными уплатами. Определите размер ежемесячного платежа. Задача 6. Финансовый инструмент на сумму S млн. руб., срок платежа по которому наступает через 4 года, продан с дисконтом по учётной ставке d% годовых. Какова сумма дисконта? S=25; d=15%. Задача 7. Переводный вексель (тратта) выдан на сумму 100 000 руб. с уплатой 15.10. Владелец векселя учёл его в банке раньше 10.09 по учетной ставке 20%. Определить получаемую при учёте сумму и дисконт. Задача 8. Покупатель купил в кредит костюм стоимостью 9000 руб. и уплатил в момент приобретения 2000 руб., а на остальную сумму получил кредит на 6 месяцев под 12% годовых на условии гашения долга равными ежемесячными уплатами. Определите размер ежемесячного платежа. Задача 9. Кредитор предоставил сумму в размере 4,5 млн. руб. с условием погашения долга через 100 дней в размере 5 млн. руб. Определить доходность операции для кредитора в виде простой и учетной ставок процентов. Задача 10. Вексель выдан на сумму S тыс. руб.владелец учел его в банке за t дней до погашения по учетной ставке d% годовых. Определить полученную владельцем сумму P и дисконт банка D для точных и приближенных процентов. S=18, t=30, d=20% Контрольные вопросы Виды финансово - коммерческих операций. Роль фактора времени в операциях. Понятие процента. Виды процентных ставок. Показатели финансовых операций. Модели связей показателей операций. Наращенная сумма множитель наращения. Модель развития операций по схеме простых процентов. Модели реинвестирования. Переменные процентные ставки. Схемы вложения денег в банк и модели расчета. Математическое дисконтирование. Коммерческий учет. Учетные ставки. Практическая работа №2 Сложные проценты. Цель: разобрать понятие сложных процентов, сущность операции дисконтирования, понятие учетной ставки, научиться работать с формулами. Теоретические обоснования При начислении сложных процентов по ставке i за базу берется сумма долга с начисленными на нее в предыдущем периоде процентами. Наращенная сумма S есть степенная функция. Таблица 4 Сложные проценты, наращение
Сложные проценты, дисконтирование
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

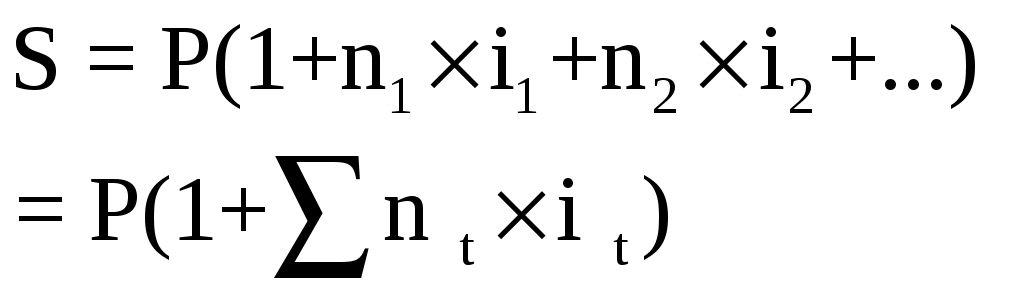 (5)
(5)