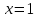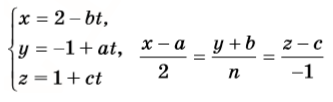|
СОР 11. Тема Показательная функция, ее свойства и график. Логарифм числа и его свойства. Логарифмическая функция, ее свойства и график. Производная и интеграл показательной функции. Производная логарифмической функции
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ»
Тема
|
Показательная функция, ее свойства и график. Логарифм числа и его свойства. Логарифмическая функция, ее свойства и график. Производная и интеграл показательной функции. Производная логарифмической функции.
|
Цели обучения
|
11.4.1.14 Знать определение показательной функции и строить ее график
11.4.1.17 Знать свойства логарифмов и применять их для преобразования логарифмических выражений
11.4.1.18 Знать определение логарифмической функции и строить ее график
11.4.1.20 Находить производную и интеграл показательной функции
11.4.1.21 Находить производную логарифмической функции
|
Критерии оценивания
|
Обучающийся
Строит график показательной функции;
Применяет свойства логарифмов для преобразования логарифмических выражений;
Применяет определение логарифмической функции при построении ее графика;
Находит производные показательной и логарифмической функций;
Находит интеграл показательной функции .
|
Уровень мыслительных навыков
|
Применение
|
Время выполнения
|
30 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
Количество баллов
|
4
|
5
|
3
|
5
|
Всего баллов
|
17 баллов
|
1 ВАРИАНТ
Постройте график функций:
а)  , б) , б) 
2.Найдите значение выражения : 
3.Найдите производную функции :
4. Вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц):
 , , 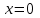 , ,  , , . .
2 ВАРИАНТ
1.Постройте график функций:
а)  , б) , б)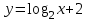
2.Найдите значение выражения: 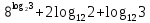
3.Найдите производную функции: 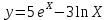
4.Вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц):
 , ,  , , 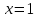 . .
ВАРИАНТ
1.Постройте график функций:
а) , б) у = , б) у = 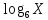 . .
2.Найдите значение выражения: 
3.Найдите производную функции :
4.Вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц):
 , ,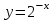 , ,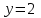 . .
4 ВАРИАНТ
1.Постройте график функций:
а) у =  , б) , б) 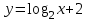
2.Найдите значение выражения 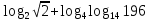
3.Найдите производную функции у = ln (2x – 11)+5Х
4.Вычислите площадь фигуры, ограниченной линиями (ответ округлите до единиц):
 у=3-Х у=3-Х 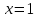
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Строит график показательной или логарифмической функции
|
1
|
определяет вид функции;
|
1
|
составляет и заполняет таблицу значений для заданной функции;
|
1
|
находит область определения функции;
|
1
|
строит график заданной функции;
|
1
|
Применяет свойства логарифмов для преобразования логарифмических выражений
|
2
|
использует определение логарифма;
|
1
|
применяет свойства степени логарифмов
|
1
|
использует основное логарифмическое тождество.
|
1
|
применяет свойства логарифмов;
|
1
|
вычисляет значение выражения;
|
1
|
Находит производные показательной и логарифмической функций
|
3
|
Применяет формулу нахождения производной показательной функции;
|
1
|
Применяет правила нахождения производных;
|
1
|
применяет формулу нахождения производной логарифмической функции;
|
1
|
Находит интеграл показательной функции
|
4
|
изображает данные линии на координатной плоскости и выделяет, интересующую нас фигуру
|
1
|
применяет свойства определенного интеграла;
|
1
|
находит интеграл показательной функции;
|
1
|
применяет формулу Ньютона-Лейбница;
|
1
|
Находит площадь фигуры
|
1
|
Итого:
|
17
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ
«ПРИМЕНЕНИЕ УРАВНЕНИЙ ПРЯМЫХ И ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ.»
Тема
|
Взаимное расположение прямой и плоскости в пространстве
Расстояние от точки до плоскости в пространстве
Нахождение угла между двумя прямыми в пространстве
|
Цели обучения
|
11.2.6 Знать взаимное расположение прямой и плоскости в пространстве
11.4.1 Знать формулу нахождения расстояния от точки до плоскости, применять ее при решении задач
11.4.2 Находить угол между прямыми (по заданным уравнениям прямых)
11.4.3 Применять условие параллельности и перпендикулярности прямых в пространстве при решении задач
|
Критерии оценивания
|
Обучающийся
Определяет взаимное расположение прямой и плоскости в пространстве
Определяет расстояние от точки до плоскости
Находит угол между прямыми в пространств
Применяет условие параллельности и перпендикулярности прямых в пространстве
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
20 мин
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
5
|
Количество баллов
|
1
|
3
|
3
|
3
|
3
|
итого
|
13 баллов
|
1 ВАРИАНТ
Определите взаимное расположение прямой и плоскости: x = –1 + 2t, y = 3 + 4t, z = 3t и 2x – 2y + z – 5 = 0
Найдите расстояние от точки A(1; 2; 3) до плоскости: 3x – y – 3z – 3 = 0
Треугольная пирамида АВСD задана координатами своих вершин: А(d; 0; –3), B(0; 3; c), C(–2; b; 3), D(2; –3; a). Найдите: угол между прямыми АВ и АС.
По условию 3 задания найти: угол между прямой АД и плоскостью АВС.
При каких значениях n прямые перпендикулярны

2 ВАРИАНТ
Определите взаимное расположение прямой и плоскости:
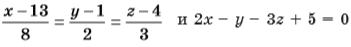
Найдите расстояние от точки A(1; 2; 3) до плоскости: 2x + y + 3z – 7 = 0
Треугольная пирамида АВСD задана координатами своих вершин: А(d; 0; –3), B(0; 3; c), C(–2; b; 3), D(2; –3; a). Найдите: ∠BAC.
По условию 3 задания найти: угол между прямой АД и плоскостью АВС
При каких значениях n прямые перпендикулярны
 
3 ВАРИАНТ
Определите взаимное расположение прямой и плоскости:
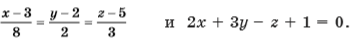
Найдите расстояние от точки A(1; 2; 3) до плоскости: 2x – y + 3z + 9 = 0
Треугольная пирамида АВСD задана координатами своих вершин: А(d; 0; –3), B(0; 3; c), C(–2; b; 3), D(2; –3; a). Найдите: угол между прямыми АД и АС
По условию 3 задания найти: угол между прямой АД и плоскостью АВС
При каких значениях n прямые перпендикулярны
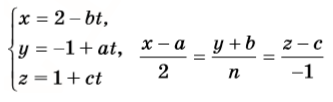
4 ВАРИАНТ
Определите взаимное расположение прямой и плоскости:
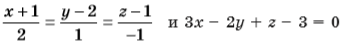
Найдите расстояние от точки A(1; 2; 3) до плоскости: 3x – 4y + 8 = 0
Треугольная пирамида АВСD задана координатами своих вершин: А(d; 0; –3), B(0; 3; c), C(–2; b; 3), D(2; –3; a). Найдите: угол между прямыми ВД и ВС.
По условию 3 задания найти: угол между прямой АД и плоскостью АВС
При каких значениях n прямые перпендикулярны

Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Определяет взаимное расположение
прямой и плоскости в пространстве.
|
1
|
использует скалярное произведение и условие перпендикулярности векторов
|
1
|
Определяет расстояние от точки до плоскости.
|
2
|
составляет уравнение прямой l, проходящей через точку А перпендикулярно плоскости α;
|
1
|
определяет точку пересечения В прямой l с плоскостью α
|
1
|
находит расстояние от точки А до точки В.
|
1
|
Определяет угол между прямыми в пространстве.
|
3
|
Определяет направяющие векторы прямых
|
1
|
Знает и применяет формулы нахождения угла между прямыми
|
1
|
Определяет угол между данными прямыми
|
1
|
Определяет угол между прямой и плоскостью в пространстве
|
4
|
Находит координаты направляющего вектора прямой АD и координаты вектора нормали плоскости АВС
|
1
|
Знает и применяет алгоритм нахождения угла между прямой и плоскостью
|
1
|
Находит синус угла между прямой и плоскостью
|
1
|
Применяет условие перпендикулярности прямых в пространстве.
|
5
|
Определяет направляющие векторы прямых
|
1
|
Записывает условие перпендикулярности векторов
|
1
|
Из полученного уравнения находит нужное значение n
|
1
|
Общий балл
|
13
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ
«ПРИМЕНЕНИЕ УРАВНЕНИЙ ПРЯМЫХ И ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ»
ФИ ОБУЧАЮЩЕГОСЯ _______________________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Определяет взаимное расположение прямой и плоскости в пространстве.
|
Затрудняется в определении взаимное расположение прямой и плоскости в пространстве
|
Допускает ошибки в определении взаимного расположения прямой и плоскости в пространстве.
|
Определяет взаимное расположение прямой и плоскости в пространстве
|
Определяет расстояние от точки до плоскости.
|
Затрудняется в нахождении расстояния от точки до плоскости
|
Применяет формулу расстояния от точки до плоскости, допускает вычислительные ошибки.
|
Находит расстояние от точки до плоскости.
|
Находит угол между прямыми в пространстве.
|
Затрудняется в нахождении угла между прямыми в пространстве.
|
Использует скалярное произведение для нахождения угла между прямыми в пространстве, допускает вычислительные ошибки.
|
Определяет косинус угла между прямыми в пространстве.
|
Находит угол между прямой и плоскостью в пространстве
|
Затрудняется в нахождении угла между прямой и плоскостью в пространстве.
|
Использует скалярное произведение для нахождения угла между прямой и плоскостью в пространстве, допускает вычислительные ошибки.
|
Определяет синус угла между прямой и плоскостью в пространстве.
|
Применяет условие перпендикулярности прямых в пространстве.
|
Затрудняется в применении условия перпендикулярности прямых в пространстве
|
Использует скалярное произведение для установления перпендикулярности прямых в пространстве, допускает вычислительные ошибки.
|
Применяет условие перпендикулярности прямых в пространстве при решении задач
| |
|
|
 Скачать 2.26 Mb.
Скачать 2.26 Mb. , б)
, б) 


 ,
, 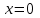 ,
,  ,
, .
. , б)
, б)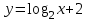
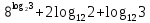
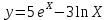
 ,
,  ,
, 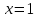 .
. , б) у =
, б) у = 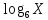 .
.

 ,
,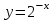 ,
,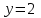 .
. , б)
, б) 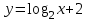
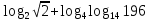
 у=3-Х
у=3-Х