|
|
СОР 11. Тема Показательная функция, ее свойства и график. Логарифм числа и его свойства. Логарифмическая функция, ее свойства и график. Производная и интеграл показательной функции. Производная логарифмической функции
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТЕЛА ВРАЩЕНИЯ И ИХ ЭЛЕМЕНТЫ»
Тема
|
Цилиндр и его элементы. Развертка, площадь боковой и полной поверхности цилиндра. Конус и его элементы. Развертка, площадь боковой и полной поверхности конуса. Касательная плоскость к сфере
|
Цели обучения
|
11.1.11 Уметь выполнять развёртки многогранников и тел вращений
11.3.4 Выводить формулы площади боковой и полной поверхности цилиндра и применять их при решении задач
11.3.6 Выводить формулы площади боковой и полной поверхности конуса и применять их при решении задач
11.4.4 Решать задачи на взаимное расположение плоскости и сферы в координатах
11.3.5 Решать задачи на нахождение элементов тел вращения (цилиндра, конуса, усеченного конуса, шара)
|
Критерии оценивания
|
Обучающийся
Распознает развертки тел вращения
Находит площадь поверхности конуса и площадь поверхности цилиндра
Решает задачи на взаимное расположение плоскости и сферы в координатах
Находит элементы конуса
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
30 мин
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
Количество баллов
|
4
|
8
|
4
|
итого
|
16 баллов
|
1 ВАРИАНТ
1. а) Определите по развертке тело.

b) Вычислите площади боковой и полной поверхности
3. Сфера задана уравнением (x+1)2 + y2 +(z-3)2 = 25.
а) Покажите, что точка A(-1;3; -1) принадлежит сфере.
Запишите координаты вектора ОА, где О — центр сферы.
Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку А
Найдите расстояние от центра сферы до плоскости 2x- y+2z-5=0 и определите взаимное расположение сферы и данной плоскости.
Периметр осевого сечения конуса равен 9 см, а угол развертки боковой поверхности 450. Найдите высоту конуса.
2 ВАРИАНТ
а) Определите по развертке тело.

b) Вычислите площади боковой и полной поверхности
Сфера задана уравнением x2 + (y-2) 2 +(z-3)2 = 16.
а) Покажите, что точка В(0;2; -1) принадлежит сфере.
Запишите координаты вектора ОВ, где О — центр сферы.
с) Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку В.
Найдите расстояние от центра сферы до плоскости x- y+z-1=0 и определите взаимное расположение сферы и данной плоскости.
Периметр осевого сечения конуса равен 18 см, а угол развертки боковой поверхности 900 . Найдите высоту конуса.
ВАРИАНТ
а) Определите по развертке тело.

b) Вычислите площади боковой и полной поверхности, если L=8 см, RB = 3см, RH =6 см.
Сфера задана уравнением (x+2)2 + (y-1) 2 +z2 = 9.
а) Покажите, что точка С(1;1; 0) принадлежит сфере.
Запишите координаты вектора ОС, где О — центр сферы.
Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку С.
Найдите расстояние от центра сферы до плоскости x+ y-z-2=0 и определите взаимное расположение сферы и данной плоскости.
Периметр осевого сечения конуса равен 12 см, а угол развертки боковой поверхности 600 . Найдите высоту конуса.
ВАРИАНТ
а) Определите по развертке тело.

b) Вычислите площади боковой и полной поверхности, если L=10 см, RB = 5см, RH =7 см.
Сфера задана уравнением (x-3)2 + (y+4) 2 +z2 = 25.
Покажите, что точка D(3;1; 0) принадлежит сфере.
b) Запишите координаты вектора ОD, где О — центр сферы.
с) Составьте общее уравнение плоскости, касательной к сфере, проходящей через точку D.
Найдите расстояние от центра сферы до плоскости 2x+ y-z-1=0 и определите взаимное расположение сферы и данной плоскости.
Периметр осевого сечения конуса равен 6 см, а угол развертки боковой поверхности 300 . Найдите высоту конуса.
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Распознает развертки тел вращения.
|
1 a
|
записывает название фигуры на первом рисунке;
|
1
|
Находит площадь
поверхности конуса и площадь поверхности
цилиндра.
|
1 b
|
определяет радиус окружности;
|
1
|
находит площадь поверхности цилиндра;
|
1
|
находит площадь поверхности конуса;
|
1
|
Решает задачи на
взаимное расположение плоскости и сферы в координатах.
|
2
|
показывает принадлежность точки А сфере;
|
1
|
указывает координаты центра сферы;
|
1
|
находит координаты вектора ОА;
|
1
|
подставляет координаты вектора-
нормали в общее уравнение плоскости;
|
1
|
подставляет координаты точки А в общее уравнение плоскости;
|
1
|
записывает общее уравнение плоскости;
|
1
|
применяет формулу расстояния от точки до плоскости;
|
1
|
находит расстояние и делает вывод о взаимном расположении сферы и плоскости;
|
1
|
Находит элементы конуса.
|
3
|
использует периметр сечения и выражает через неизвестную радиус и образующую конуса;
|
1
|
использует формулу для нахождения длины дуги, составляет уравнение;
|
1
|
находит радиус и образующую конуса;
|
1
|
находит высоту конуса.
|
1
|
Итого:
|
16
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ»
Тема
|
Параллельные прямые, их признаки и свойства. Сумма углов треугольника. Внешний угол треугольника. Признаки равенства прямоугольных треугольников. Свойства прямоугольного треугольника .
|
Цели обучения
|
7.1.2.5 Применять признаки параллельности прямых при решении задач
7.1.1.17 Применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач
7.1.1.19 Применять теорему о внешнем угле треугольника
7.1.1.27 Применять свойства прямоугольного треугольника
|
Критерии оценивания
|
Обучающийся
Определяет параллельность прямых, используя признаки параллельности
Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач
Применяет свойства прямоугольного треугольника при решении задач
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
Количество баллов
|
3
|
5
|
3
|
итого
|
12 баллов
|
1 ВАРИАНТ
 
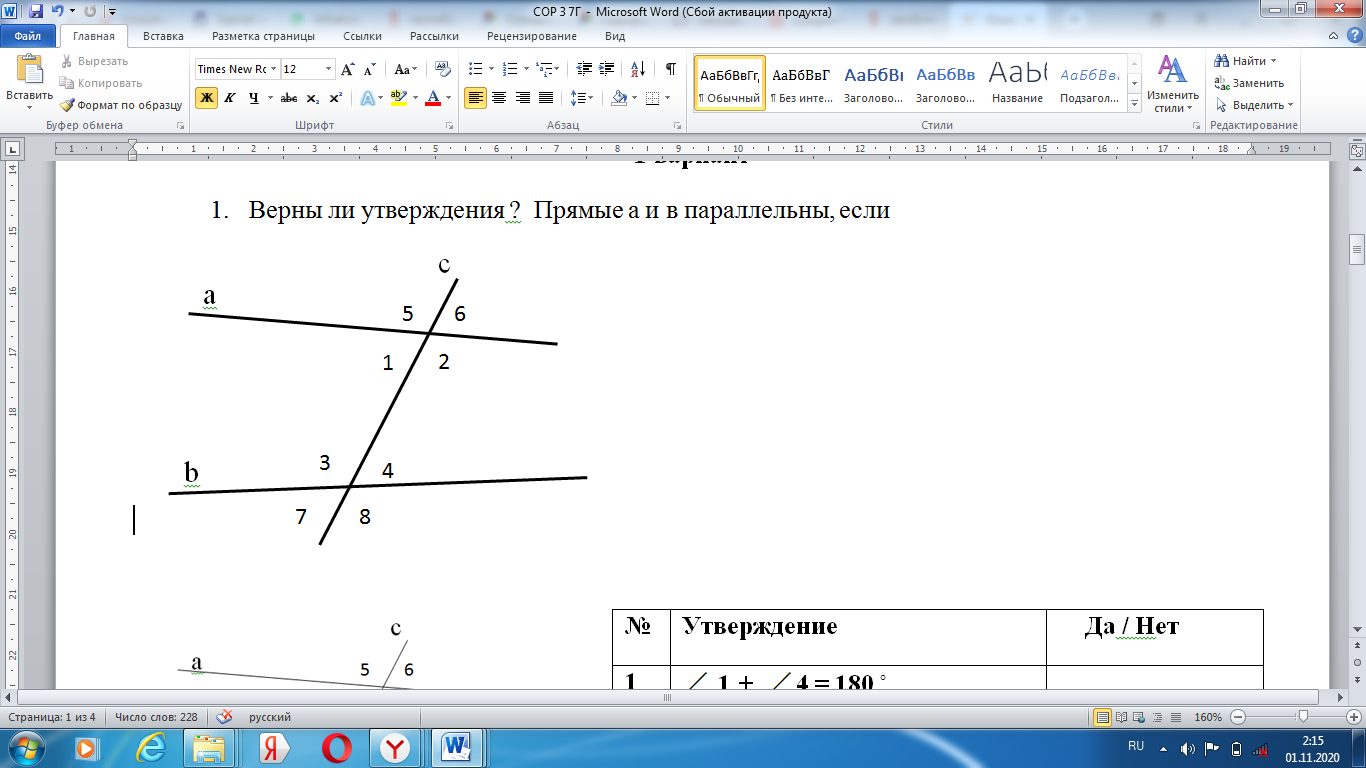
Верны ли утверждения ? Прямые а и b параллельны, если
№
|
Утверждение
|
Да / Нет
|
1
|
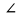 1 + 1 + 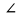 4 = 180 ◦ 4 = 180 ◦
|
|
2
|
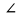 5 = 5 = 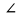 3 3
|
|
3
|
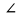 2 + 2 + 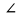 4 = 180 ◦ 4 = 180 ◦
|
|
4
|
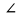 6 = 6 = 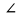 7 7
|
| |
|
|
 Скачать 2.26 Mb.
Скачать 2.26 Mb.







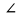 1 +
1 +