!_МУ для лаб. Методические указания для выполнения лабораторных работ по теме анализ и моделирование деятельности организации с целью принятия управленческих решений
 Скачать 2.84 Mb. Скачать 2.84 Mb.
|
Пример выполнения задачи прогнозированияПрогноз произведем на основании уравнения регрессии (применения функции ЛИНЕЙН в задаче прогнозирования)1-способ Менеджер условного офиса решил построить регрессионное уравнение (модель), прогнозирующее продажи одной из книг. В его распоряжении были данные по продажам этой книги за последние 10 недель. Агенты офиса фиксировали также уровень рекламы и количество конкурирующих товаров (книг на аналогичную тему). Используя функцию ЛИНЕЙН, менеджер построил уравнение множественной регрессии. На рис.3.1 показан лист рабочей книги Excel, где размещены данные о продажах и где построено уравнение регрессии, основываясь на этих данных: Примечание: Формулу необходимо ввести как формулу массива в первую ячейку. Потом выделяется весь диапазон, нажимается F2, а затем Ctrl+Shift+Enter.  Рис. 3.1. Построение уравнения регрессии по данным продаж Менеджер построил это уравнение дважды, получив два уравнения - Y1 и Y2, используя выборки измерений разного объема (см. данные на рис.). Этот полезный прием позволяет понять, насколько полученные коэффициенты критичны к измерениям. Менеджер достаточно тщательно проанализировал все данные, возвращаемые функцией ЛИНЕЙН для двух ее вызовов. Обратите внимание, массивы результатов работы функции на рисунке 3.1 подсвечены. С содержательной точки зрения важен следующий полученный результат. Оба измеряемых параметра - уровень рекламы и число конкурирующих книг - являются статистически значимыми. Большее влияние на уровень продаж оказывает число книг - конкурентов. Менеджер решил использовать полученные уравнения как для прогноза будущих продаж, так и для принятия таких решений, как, скажем, повышение уровня рекламы. Чтобы визуально увидеть влияние уровня рекламы на продажи, менеджер использовал полученные уравнения для построения графиков Y1(U) и Y2(U) при фиксированных значениях параметров T и V. Результаты работы можно увидеть на рисунке 3.2. 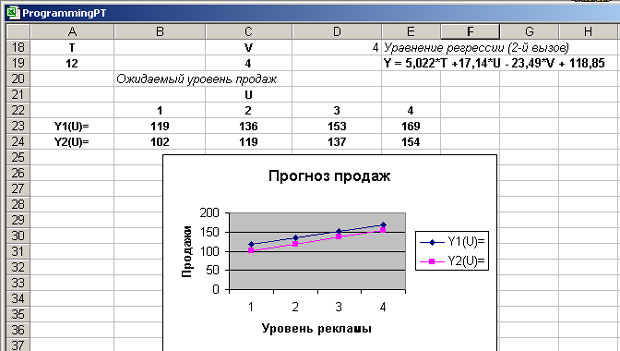 Рис. 3.2. Прогнозирование продаж в зависимости от уровня рекламы Полученные графики наглядно показывают, что при переходе от первого уровня рекламы к четвертому можно в полтора раза повысить продажу книг. Это предложение экономически целесообразно и менеджер представил его для принятия решений руководителю организации. 2- способ построения регрессии с использованием раздела меню Сервис – Анализ данных. Выполнить самостоятельно! 2.2. Функция ТЕНДЕНЦИЯВ основе всех других функций Excel, используемых для прогноза и регрессионного анализа лежит функция ЛИНЕЙН. Так, если уравнение регрессии уже построено, вычислить значение в новой точке нетрудно. Функция ТЕНДЕНЦИЯ решает эту простую задачу. Она неявно вызывает функцию ЛИНЕЙН и, используя полученные оценки параметров, вычисляет прогнозируемые значения в новых точках. Обращение к ней имеет вид: ТЕНДЕНЦИЯ (Известные_У, Ивестные_Х, Новые значения_Х, Конст) Здесь мы видим один новый параметр, задающий в общем случае матрицу новых значений Х. Все остальные параметры имеют тот же смысл, что и функции ЛИНЕЙН. В результате возвращается вектор прогнозных значений У, вычисленный в точках, заданных матрицей новых значений Х. Каждая ее строка задает одну точку. 2.3. Функция ПРЕДСКАЗ - частный случай функции ТЕНДЕНЦИЯ - используется в линейной модели с двумя параметрами, когда уравнение регрессии имеет вид: y = a*x + b (3.26) В этом случае Y и X представляют одномерные массивы данных. Вызов функции таков: ПРЕДСКАЗ( x; Известные_Y; Известные_X) Здесь x - точка, для которой строится прогноз. ЛГРФПРБЛ_Построение_нелинейного_уравнения_регрессии'>2.4. Функция ЛГРФПРБЛ Построение нелинейного уравнения регрессии, которое простым преобразованием сводится к задаче линейной регрессии. Такое преобразование осуществляет функция ЛГРФПРБЛ. Формально здесь используется нелинейная модель: y = b* a1x1 * a2x2 * … * amxm (3.27) Простым логарифмированием модель сводится к линейной. ln(y) = x1* ln(a1) + x2*ln(a2) + … + xm*ln(am) + b (3.28) Функция ЛГРФПРБЛ имеет те же параметры, что и функция ЛИНЕЙН. Обращение к ней: ЛГРФПРБЛ(Известные_значения_Y; Известные_значения_X; Конст; Статистика) Эта функция вызывает функцию ЛИНЕЙН, подавая ей на вход не сами измерения Y, а их логарифмы. Полученные оценки достаточно подвергнуть обратному преобразованию - взять экспоненту, и задача решена. Так строится нелинейное уравнение регрессии. Этот прием позволяет самому строить новые модели нелинейной регрессии. 2.5. Функция РОСТ Последняя из стандартных функций этого семейства - РОСТ - непосредственно вычисляет значения прогноза в новых точках, используя результаты вызова функции ЛГРФПРБЛ. РОСТ связана с функцией ЛГРФПРБЛ, как ТЕНДЕНЦИЯ связана с ЛИНЕЙН. Обращение к функции имеет вид: РОСТ(Известные_Y, Известные_X, Новые_значения_X, Конст) |
