Методические указания и индивидуальные задания для студентов технических специальностей

• Название: Методические указания и индивидуальные задания для студентов технических специальностей
• Анкор: VAiAG.doc
• Дата: 29.08.2018
• Размер: 0.84 Mb.
• Имя файла: VAiAG.doc
• Тип: Методические указания; #23762
• страница: 1 из 4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЮГО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Р ейтинговая
И нтенсивная
Т ехнология
М одульного
О бучения
ВЕКТОРНАЯ АЛГЕБРА АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Методические указания и индивидуальные задания для студентов технических специальностей
МОДУЛЬ – 2

КУРСК 2001
Составитель А.В.Бойков

УДК 519

Векторная алгебра. Аналитическая геометрия: Методические

указания и индивидуальные задания для студентов технических

специальностей / Курск.гос.техн.ун-т; Сост. А.В.Бойков. Курск,

2001. 37с.

Методические указания отражают требования образователь-

ного стандарта уровня подготовки специалистов по техническим

специальностям. Работа содержит теоретические индивидуаль-

ные упражнения, практические индивидуальные задания, кон-

трольные вопросы, указания к использованию ЭВМ, указания к

выполнению заданий, рекомендуемую литературу по темам

“Векторная алгебра” и “Аналитическая геометрия”.

Предназначены для студентов технических специальностей.
Табл. 3. Ил. 2. Библиогр.: 8 назв.

Рецензент канд. физ.-мат. наук, доцент кафедры высшей

математики В.И. Дмитриев

Текст печатается в авторской редакции

ЛР №020280 от 09. 12. 96. ПЛД № 50-25 от 1. 04.97.

Подписано в печать ________. Формат 60х84 1/16. Печать офсет-

ная. Усл. печ. л…… Уч.-изд. л…… Тираж 100 экз. Заказ ………...

Бесплатно.

Курский государственный технический университет.

Подразделение оперативной полиграфии Курского Государствен-

ного технического университета.

Адрес университета и подразделения оперативной полиграфии:

305040 Курск, ул. 50 лет Октября, 94.

СОДЕРЖАНИЕ

Введение…………………………………………………….4

1. Индивидуальные задания……………………………….5

1. 
   Теоретические упражнения……………………...…5
   
2. 
   Практические задания………………………………8
   
   1. 
      Задание 1………………………………………..8
      
   2. 
      Задание 2………………………………………..9
      
   3. 
      Задание 3………………………………………10
      
   4. 
      Задание 4………………………………………10
      
   5. 
      Задание 5………………………………………11
      
   6. 
      Задание 6………………………………………11
      
   7. 
      Задание 7………………………………………11
      
   8. 
      Задание 8………………………………………11
      
   9. 
      Задание 9………………………………………12
      
   10. 
       Задание 10……………………………………..15
       
   11. 
       Задание 11……………………………………..23
       
   12. 
       Задание 12………………………………….….24
       

2. Использование ЭВМ…………………………………...25

3. 
   Образцы выполнения некоторых заданий……………27
   
4. 
   Контрольные вопросы…………………………………35
   

Список рекомендуемой литературы…………………….37

ВВЕДЕНИЕ

Цель преподавания математики в вузе – ознакомить студен-тов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по матема-тике и ее приложениям; развить логическое мышление и повы-сить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.

Важным фактором усвоения математики и овладения ее методами является самостоятельная работа студента.

Одной из форм организации самостоятельной работы студен-тов является система РИТМО – система рейтинговой интенсив-ной технологии модульного обучения. Как показывает опыт ряда вузов нашей страны эта система активизирует самостоятельную работу студентов и способствует более глубокому изучению курса математики.

Предлагаемые методические указания являются пособием к одному из модулей системы РИТМО, используемой в течении десяти лет в преподавании математики в Курском Государствен-ном техническом университете. Методические указания посвяще-ны разделам “Векторная алгебра” и “Аналитическая геометрия” (до тем кривые и поверхности второго порядка) и содержат индивидуальные задания (теоретическое упражнение и практи-ческие задания), контрольные вопросы, рекомендуемую литера-туру, указания к использованию ЭВМ (Маthcad) при выполнении заданий модуля, образцы выполнения некоторых (наиболее труд-ных) заданий.

Предусмотрены три уровня сложности заданий модуля. Студент должен выполнить одно теоретическое упражнение и некоторое количество практических заданий, в зависимости от выбранного им (или преподавателем) уровня сложности:

первый уровень - №№ 3-5, 8, 9(а,б), 11(а,б);

второй уровень - №№ 1-9, 11(а-е,и-л);

третий уровень - №№ 1-12.

1. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Выбор индивидуального задания к модулю-2 осуществляет-ся по номеру варианта студента n. При этом используются параметр Р_к - остаток от деления номера варианта n на число к, и выражение [n / k] - целая часть от деления n на k. Например, если n = 7, то Р₂=1, Р₃=1, Р₄=3, Р₅=2, Р₆=1, Р₇=0, Р₈=7, Р₉=7 и т.д. Если n = 7 и к = 4, то [n/k] = [7/4] = 1.

При выполнении индивидуальных заданий модуля рекомен- дуется использовать следующую литературу:

[1, гл. 1, §§ 1-4; гл. 2, §§ 4-5; 2, §§ 5-14; 3, гл. 3, §§3-9; 4, гл. I-III;

5, гл.2, §§ 1-3; 6-8].

1. 
   ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
   

Выполнить теоретическое упражнение номер m, где m=P₃₀ +1.

1. Сформулировать и доказать свойства проекции вектора на ось.
2. Записать и доказать соотношения между координатами вектора
и координатами точек “начала” и “конца” вектора.
3. Сформулировать и доказать необходимое и достаточное усло-
вие коллинеарности векторов.
4. Записать и доказать формулы, выражающие координаты точки,
делящей отрезок в заданном отношении, через координаты кон-
цов этого отрезка.
5. Записать и доказать формулы для длины и направляющих коси-
нусов вектора, выражающие эти величины через декартовы ко-
ординаты вектора.
6. Доказать свойства скалярного произведения векторов.
7. Записать и доказать формулу, выражающую скалярное произ-
ведение векторов через их декартовы координаты.
8. Сформулировать и доказать необходимое и достаточное усло-
вие ортогональности векторов.
9. Записать и доказать формулы для косинуса угла между двумя

векторами в пространствах V₂ и V₃.
10. Доказать свойство [] = - [] векторного произведе-

ния векторов.

11. Используя свойства векторного произведения, доказать фор-
мулу, выражающую векторное произведение векторов через
их декартовы координаты.
12. Записать и доказать формулы для вычисления площади парал-
лелограмма и треугольника с помощью векторного произведе-
ния векторов.
13. Записать и доказать формулу, выражающую смешанное про-
изведение векторов через их декартовы координаты.
14. Доказать свойства смешанного произведения векторов.
15. Записать и доказать формулы для вычисления объема парал-
лелепипеда и треугольной пирамиды с помощью смешанного
произведения векторов.
16. Сформулировать и доказать необходимое и достаточное усло-
вие компланарности векторов пространства V₃.
17. Доказать, что любая прямая на плоскости имеет уравнение
Ах + Ву + С = 0, где = (A;B) нормальный вектор этой

прямой.
18. Вывести уравнение прямой на плоскости, проходящей через
точку М₀(х₀;у₀) с угловым коэффициентом k.
19. Доказать, что любая прямая на плоскости имеет параметри-
ческие уравнения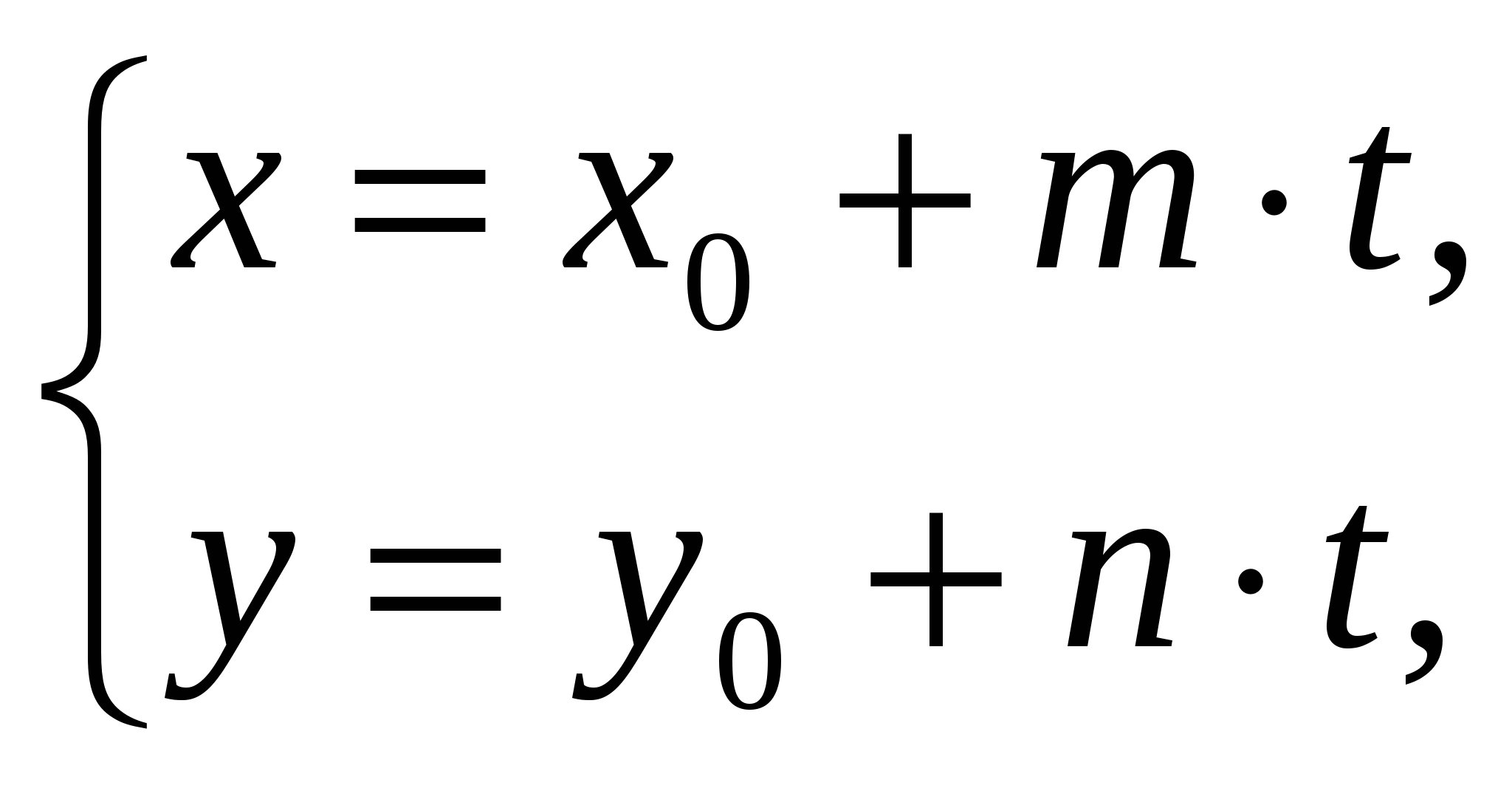
,
где (), - произвольная точка прямой, а вектор () –
направляющий вектор этой прямой. Записать каноническое
уравнение прямой.
20. Доказать, что любая прямая в пространстве имеет параметри-
ческие уравнения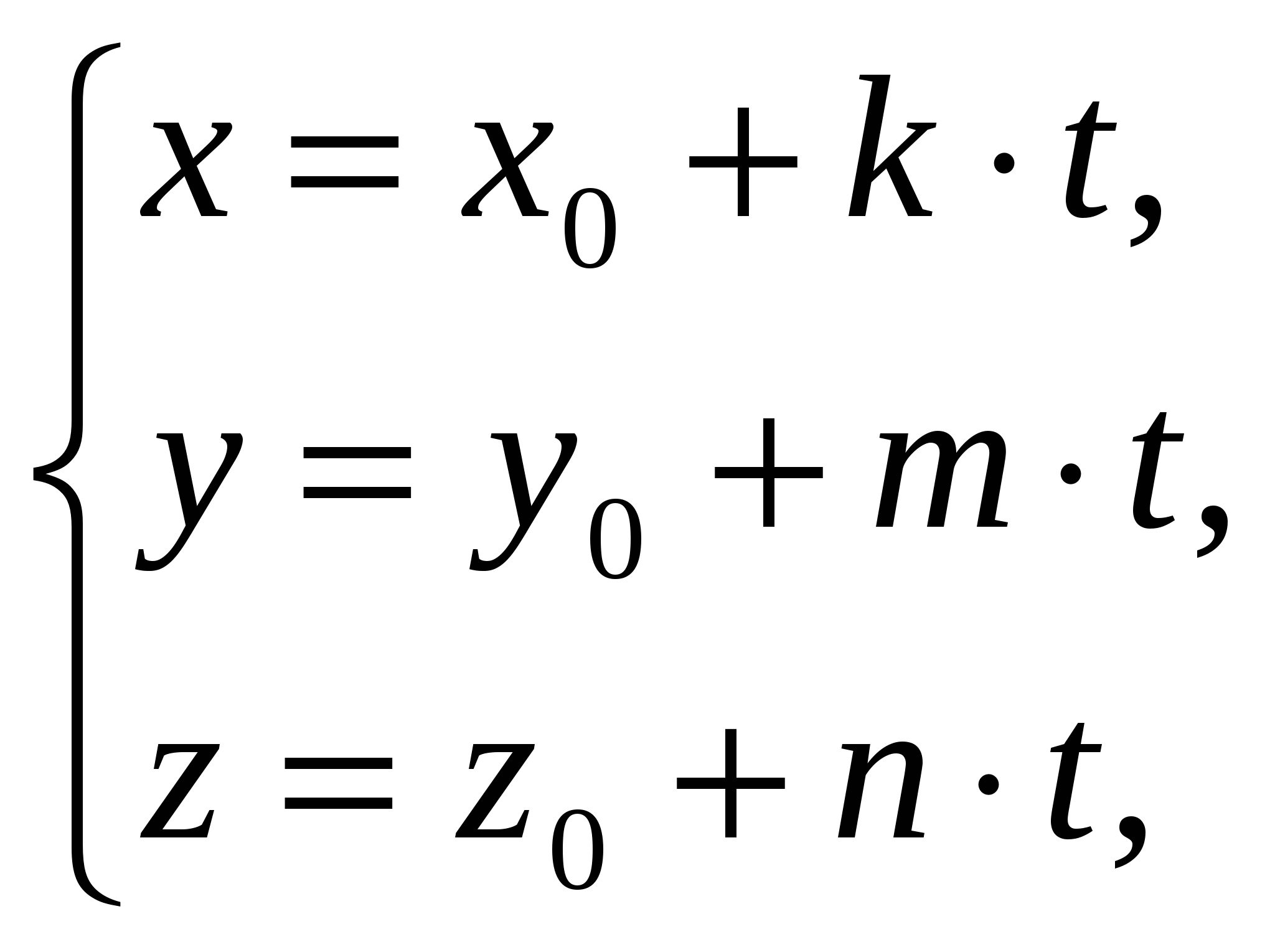




где (), - произвольная точка прямой, а вектор
() - направляющий вектор этой прямой. Записать
каноническое уравнение прямой.
21. Вывести формулу для косинуса угла между двумя прямыми

на плоскости, заданными общими уравнениями. Доказать

условия параллельности и перпендикулярности прямых.
22. Вывести формулу для тангенса угла между двумя прямыми на

плоскости, заданными уравнениями с угловым коэффициен-

том. Сформулировать и доказать условия параллельности и
перпендикулярности прямых.
23. Вывести формулу для косинуса угла между двумя прямыми на
плоскости, заданными каноническими (параметрическими )
уравнениями. Сформулировать и доказать условия параллель-
ности и перпендикулярности прямых.
24. Записать и доказать формулы для расстояния от точки до пря-
мой на плоскости и от точки до плоскости в пространстве.
25. Записать и доказать формулу для расстояния от точки до пря-
мой в пространстве.
26. Доказать, что любая плоскость в пространстве имеет уравне-
ние Ах + Ву + Сz + D = 0, где = (A;B;C) нормальный век-
тор этой плоскости.
27. Вывести уравнение плоскости проходящей через три заданные
точки, не лежащие на одной прямой.
28. Вывести формулу для косинуса угла между двумя плоскостя-
ми. Сформулировать и доказать условия параллельности и
перпендикулярности плоскостей.
29. Вывести формулу для косинуса угла между двумя прямыми в
пространстве, заданными каноническими (параметрическими)
уравнениями. Сформулировать и доказать условия параллель-
ности и перпендикулярности прямых.
30. Вывести формулу для синуса угла между прямой и плос-
костью. Сформулировать и доказать условия параллельности
и перпендикулярности прямой и плоскости.
1.2. ПРАКТИЧЕСКИЕ ЗАДАНИЯ

1.2.1. ЗАДАНИЕ 1
Решить задачу номер m из табл.1.1, где m = Р₄ +1.

Таблица 1.1

Индивидуальные условия к заданию 1

№ задачи m	Условие задачи		Угол α
1	2		3
1	А О С В	К двум тросам подве- шен груз || = 100кГ. Определить силы (в кГ), возникающие в тросах, если угол АСВ равен α, угол ОВС равен 90˚	=90˚+2˚·([n/4]+1)
2	А С В	Груз весом ||=100кГ поддерживается дву- мя стержнями АВ и СВ. Определить силы (в кГ), возникающие в стержнях, если угол АСВ равен 90˚, угол АВС равен α	α = 3·([n/4] + 1)
3	А В С	К двум тросам АС и ВС, одинаковой дли- ны, подвешен груз весом ||= 100 кГ. Определить силы (в кГ), возникающие в тросах, если угол АСВ равен α	α = 6˚·([n/4] + 1)

Продолжение табл. 1.1

1	2		3
4	С В А	Груз весом ||=100кГ поддерживается дву- мя стержнями АС и ВС. Определить силы (в кГ), возникающие в стержнях , если угол ВАС равен α, и Угол АВС равен 120˚	α = 2˚·([n/4] + 1)

1.2.2. ЗАДАНИЕ 2
Решить задачу номер m из табл.1.2, где m = Р₅ + 1

Таблица 1.2

Индивидуальные условия к заданию 2

№ задачи m	Условие задачи
1	2
1	Точка О-точка пересечения медиан треугольника АВС. Найти координаты точки В, если= (-1;Р3;0), = (1;Р5;-2), О(2;-1;Р7)
2	Точка О-точка пересечения медиан треугольника АВС. Найти координаты точки О, если А(Р3;-1;-2), С(-3;Р5;1), = (4;0;Р7)