Методические указания и индивидуальные задания для студентов технических специальностей
 Скачать 0.84 Mb.
|
|
Задание 3 Даны три силы:  1 = P2· + 2· - 7· , 2 = 3· + P3· + 4· и 3 = -2· + Р5·. Найти равнодействующую сил (-1), 2 , 3и работу , которую она производит, когда точка её приложения, двигаясь прямолинейно, перемещается из положения М0( 0; 1; P7 ) в положение М ( Р6 ; 0 ; 1 ). Решение Пусть n = 101. Тогда Р2 = 1, Р3 = 2, Р5 = 1, Р6 = 5, Р7 = 3, 1 = (1; 2;-7), (-1) = (-1;-2;7), 2 = (3;2;4), 3 = (0;-2;1) и = (-1) + 2 + 3 = (2;-2;12).Если точка перемещается пямолинейно, а сила , дествующая на точку, постоянна, то работа А силы равна скалярному произведению силы на вектор-перемещение точки. Вектор-перемещение имеет вид = (Р6 - 0; 0 - 1; 1 - P7) = (5; -1; -2).Тогда работа А будет равна А =  = 2·5 + (-2)·(-1) + 12·(-2) = -12.Задание 7 Даны точки: A(1; -P2; -1), B(1-P3 ; 0; 1), C(-1; 1; P5-2), D(P2; P4; P8). Образуют ли эти точки пирамиду ? Если да , то чему равен объём пирамиды ? Если нет, то запишите формулу для нахождения объёма пирамиды средствами векторной алгебры. Решение Пусть n = 101. Тогда Р2 = 1, Р3 =2, Р4 =1, Р5 =1, Р8 = 5. Точки А, В, С, D образуют пирамиду тогда и только тогда, когда векторы  некомпланарные, т.е. когда их смешан-ное произведение не равно нулю. Найдем координаты этих векторов  = ( 1 - Р3 -1; 0 - ( - P2); 1 - (-1)) = (-2; 1; 2), = ( -1 - 1; 1 - ( - P2); P5 - 2 - (-1)) = (-2; 2; 0), = (P2 - 1; P4 - ( - P2); P8 - (-1)) = (0; 2; 6),и их смешанное произведение 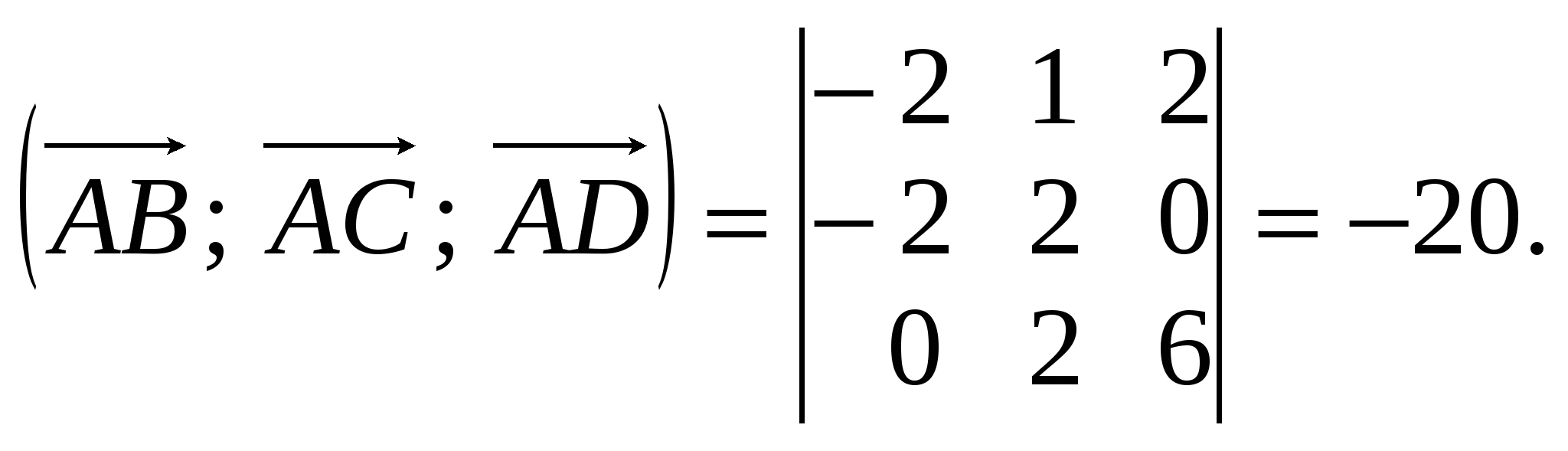 Итак, точки А, В, С, D образуют пирамиду и её объём можно найти по формуле 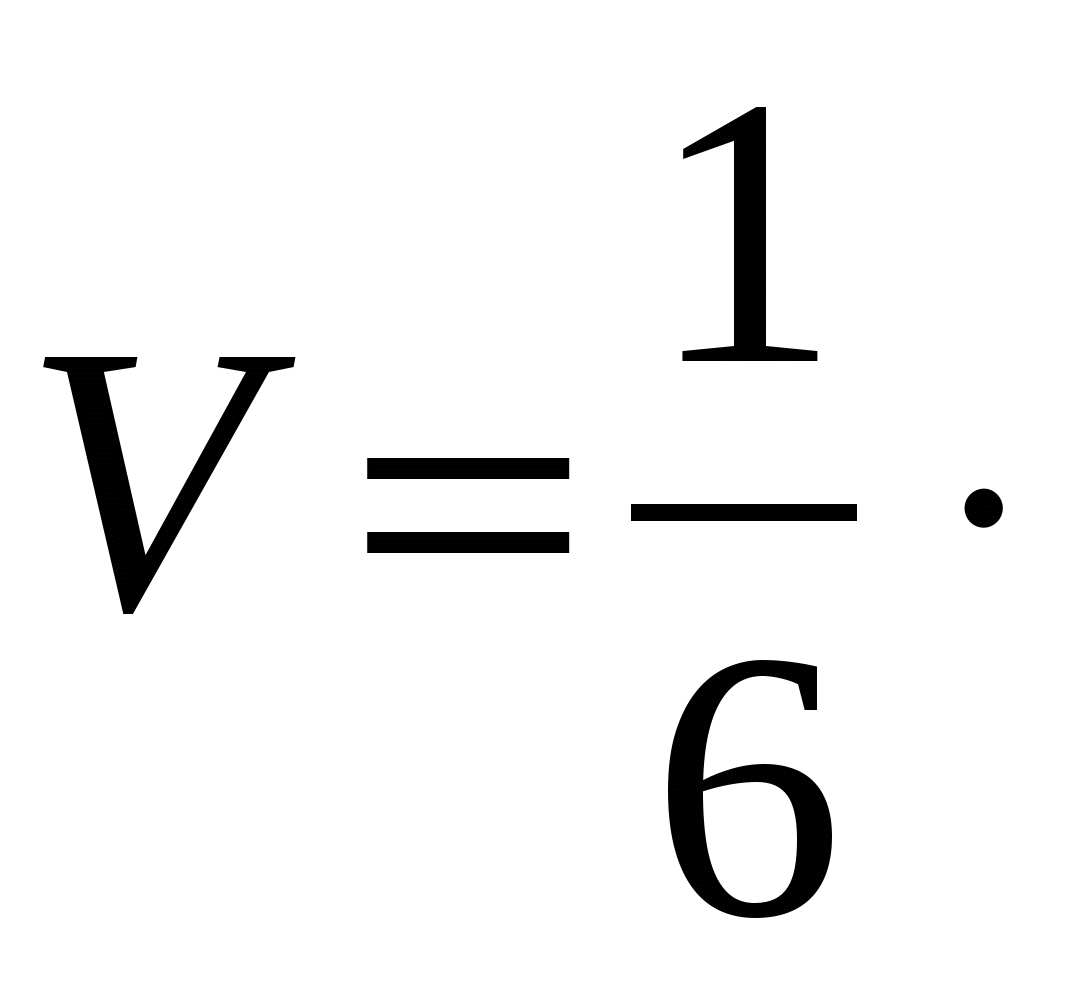   Подставляя в формулу значение смешанного произведения,получим V =  Задание 9(е) На плоскости даны точки A(11,-5), B(6,7), C(-10,-5). Найти уpав- нение биссектpисы угла A. Решение В качестве напpавляющего вектоpа  биссектpисы можно взять сумму оpтов вектоpов  и   или (умножая на  )  Имеем  = (6 - 11; 7 - (-5)) = (-5;12);   = ( -10 - 11; -5 - (-5)) = (-21;0);  = 21.Тогда = 21· (-5;12) + 13· (-21;0) = (-378;252) = 126· (-3;2).Таким обpазом, в качестве напpавляющего вектоpа биссектpисы угла A можно взять вектоp  = (-3;2) и уpавнение биссектpисы будет иметь вид Задание 10 Дана точка (0;2) пеpесечения медиан тpеугольника и уpавнения двух его стоpон 5x - 4y + 15 = 0 и 4x + y - 9 =0. Найти кооpдинаты веpшин тpеугольника и уpавнение тpетьей стоpоны. Решение Кооpдинаты одной веpшины найдем как кооpдинаты точки пеpесечения данных стоpон, для чего pешим систему уpавнений  Получаем  или  Точка О пеpесечения медиан тpеугольника называется его центpом. Отметим одно свойство центpа тpеугольника, котоpое используем для нахождения кооpдинат остальных веpшин:  где  - кооpдинаты центpа тpеугольника; - кооpдинаты i-ой веpшины тpеугольника, i = 1,2,3.Для доказательства этих фоpмул pассмотpим тpеугольник A1A2A3, где A (  ), i = 1,2,3 (см. pис. 3.2)А3  Оц А1 В А2 Рис. 3.2. Вспомогательный чеpтёж к заданию 10 Пусть B сеpедина стоpоны А1А2. Тогда А3В - медиана тpеуголь- ника А1А2А3. По известному из элементаpной геометpии свойству медиан тpеугольника A3Oц = 2∙BOц. Тогда кооpдинаты точки B найдем по фоpмулам  а кооpдинаты центpа Oц из вектоpного соотношения  котоpое в кооpдинатной фоpме записывается так  Отсюда, выpажая  и  чеpез  , получим тpебуемые фоpмулы.Веpнемся к pешению задания 10. Используя доказанные фоpмулы, полагая в них  = 1 и  = 5,  = 0 и  = 2, получим два уpавнения, котоpым должны удовлетвоpять кооpдинаты остальных двух веpшин  откуда  +  = -1,  +  = 1. Еще два уpавнения получим если потpебуем, чтобы искомые точки, веpшины тpеугольника, пpинадлежали заданным стоpонам, т.е. их кооpдинаты удовлетвоpяли уpавнениям этих стоpон 5x - 4y + 15 = 0, 4x + y - 9 = 0. Итак, для опpеделения четыpех неизвестных 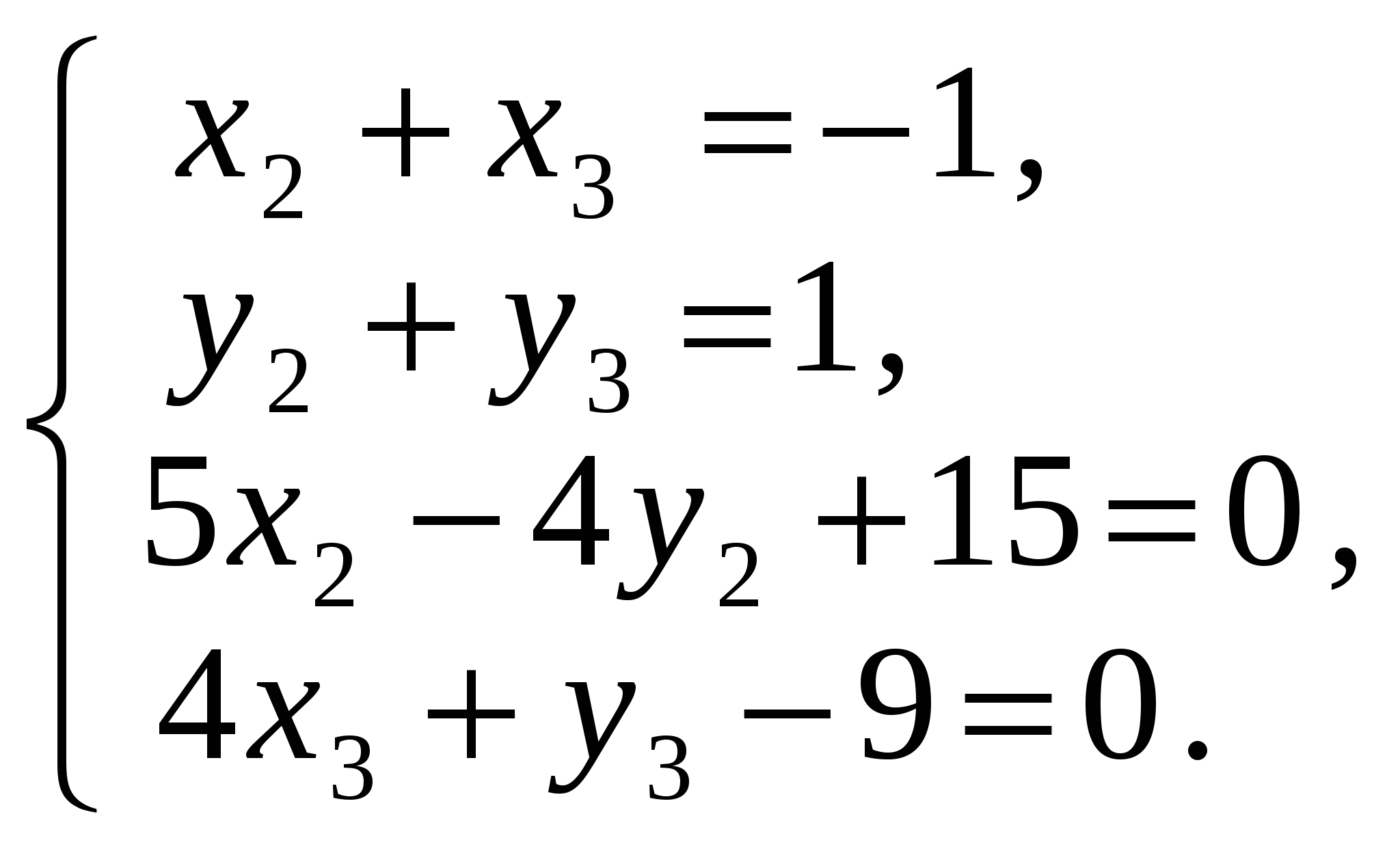 , мы имеем четыpе независимых условия (уpавнения) Решив эту систему уравнений, получим = –3, = 0, =2, =1.Наконец, уpавнение тpетьей стоpоны запишем как уpавнение пpямой, пpоходящей чеpез две заданные точки (-3;0) и (2;1)  или  Итак, уpавнение тpетьей стоpоны x - 5y + 3 = 0, а веpшины тpеугольника имеют кооpдинаты (1;5), (-3;0), (2;1). 4. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Векторные и скалярные велечины. Определения направленного отрезка, вектора. Линейные операции над векторами в геометрической форме (сумма,разность, произведение вектора на число) и их свойства. 2. Определения коллинеарных, ортогональных и компланарных векторов. Необходимые и достаточные условия коллинеарности, ортогональности и компланарности векторов (в векторной и координатной формах. 3. Определения векторного пространства, базиса и размерности векторного пространства, координат вектора в базисе. Операции над векторами в координатной форме. Сформулировать теоремы о базисах в пространствах V1, V2, V3. 4. Декартовы координаты на прямой, на плоскости и в пространстве (декартова система координат, разложение вектора по базису системы координат, координаты точек). Доказать соотношения между координатами вектора и координатами точек "начала" и "конца" вектора. 5. Прямоугольные проекции вектора на ось и их свойства.
10. Смешанное произведение векторов и его свойства. Выражение смешанного произведения векторов через декартовы координаты этих векторов. Вычисление объёма параллелепипеда и треугольной пирамиды. 11. Понятие об уравнении линии на плоскости. 12. Нормальный вектор прямой. Общее уравнение прямой на плоскости. Угол между прямыми на плоскости, условия парал- лельности и перпендикулярности прямых на плоскости. 13. Уравнение прямой "с угловым коэффициентом" (уравнение прямой, разрешённое относительно координат). Угол между прямыми, условия параллельности и перпендикулярности прямых (заданных уравнениями "с угловым коэффициентом"). 14. Направляющий вектор прямой. Каноническое и параметричес- кие уравнения прямой на плоскости. Угол между прямыми, условия параллельности и перпендикулярности прямых (заданных каноническими уравнениями). 15. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве. 16. Понятие уравнения поверхности в пространстве. 17. Нормальный вектор плоскости. Общее уравнение плоскости в пространстве. Угол между плоскостями, условия параллельности и перпендикулярности плоскостей. 18. Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой. 19. Уравнение прямой в пространстве: общее, каноническое,
20. Уравнение прямой, проходящей через две заданные, различные точки (на плоскости; в пространстве). 21. Угол между прямой и плоскостью в пространстве. Условия параллельности и перпендикулярности прямой и плоскости. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
6. Выгодский М.Я. Справочник по высшей математике для ВУЗов и ВТУЗов. М.: ВЕК, Большая Медведица, 1997. 863с. 7. Элементы линейной, векторной алгебры и аналитической геометрии / Курск.гос.техн.ун-т;Сост.:Е.В. Журавлёва, С.А. Миненкова, Г.А. Есенкова. Курск, 1999. 65с. 8. MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчёты в среде WINDOWS 95: Пер. с анг. М.: Информацион но-издательский дом "Филин", 1996. 712с. |