Методические указания и индивидуальные задания для студентов технических специальностей
 Скачать 0.84 Mb.
|
1.Вызов шаблона вектора и его ввод Из окна матричной и векторной палитры вызвать панель ввода матрицы. Для этого щелкнуть (левой кнопкой мыши) по кнопке Указать размеры n,1 матрицы в соответствующих полях откры- вающейся панели и щелкнуть по кнопке ОК (n - размерность вектора, число строк; 1 - число столбцов). Набрать матрицу-вектор, передвигаясь с помощью кнопок со стрелками. После набора последнего числа нажать клавишу ПРОБЕЛ. 2. Операции над векторами Операции над векторами можно выполнять используя кнопки матричной и векторной палитры, калькулятора и клавиатуры. Последовательность действий иллюстрирует следующий пример. ПРИМЕР 2.1 Введём векторы 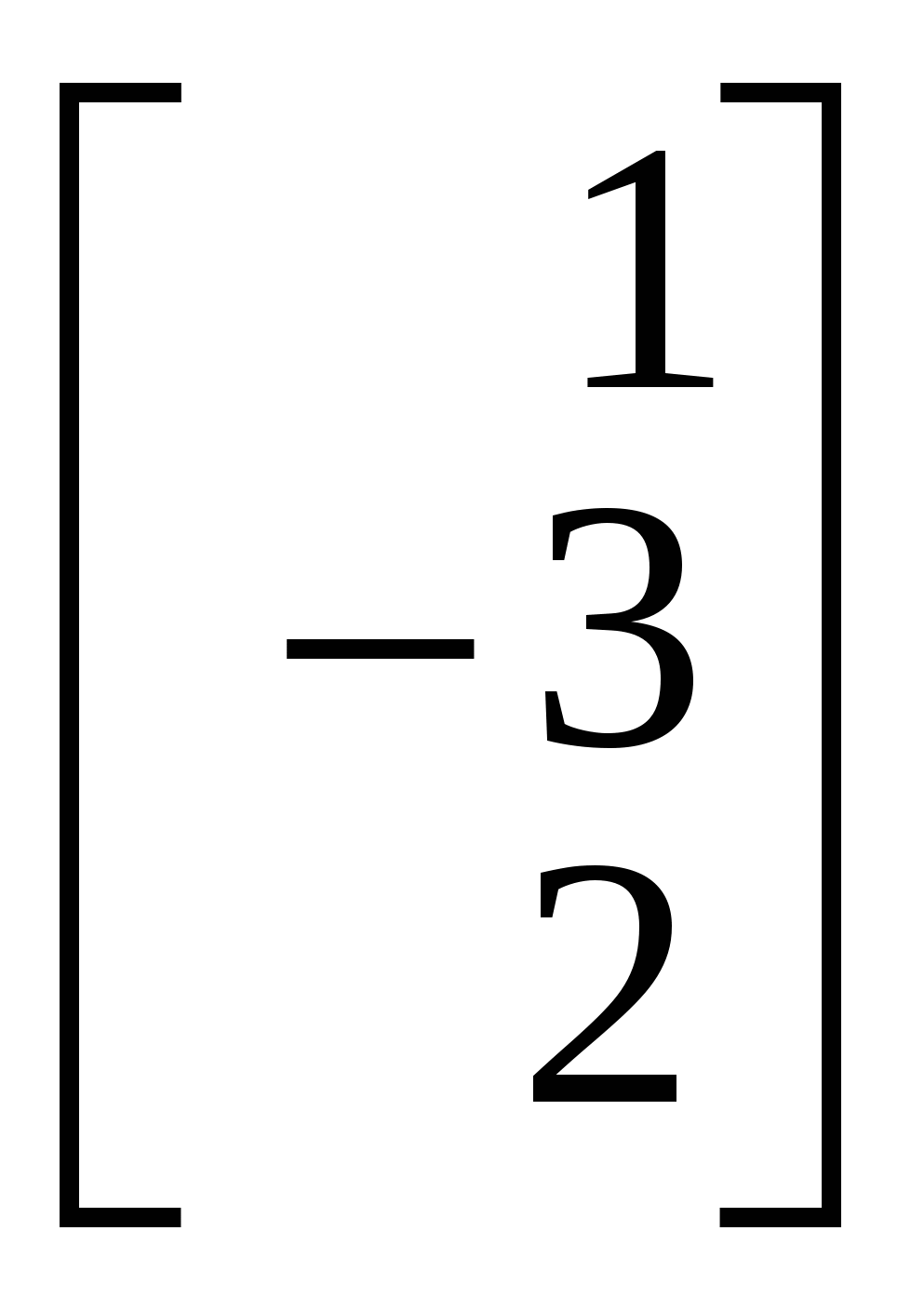 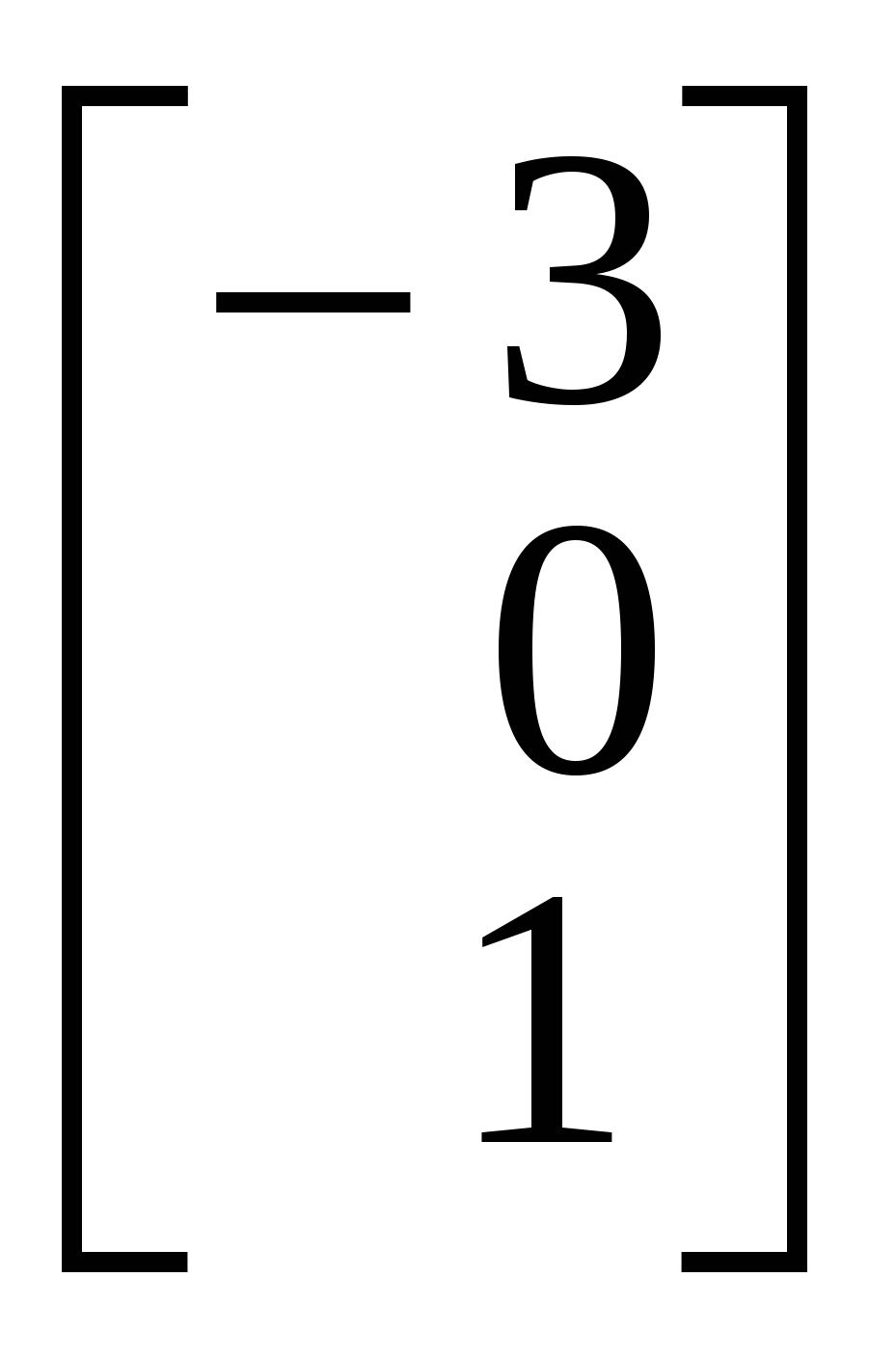и число λ = -1.5:  ;   ; λ = -1.5.Найдем сумму  и разность  векторов  и  , произведение вектора  на число λ, скалярное ( ) и векторное ( )произведения векторов 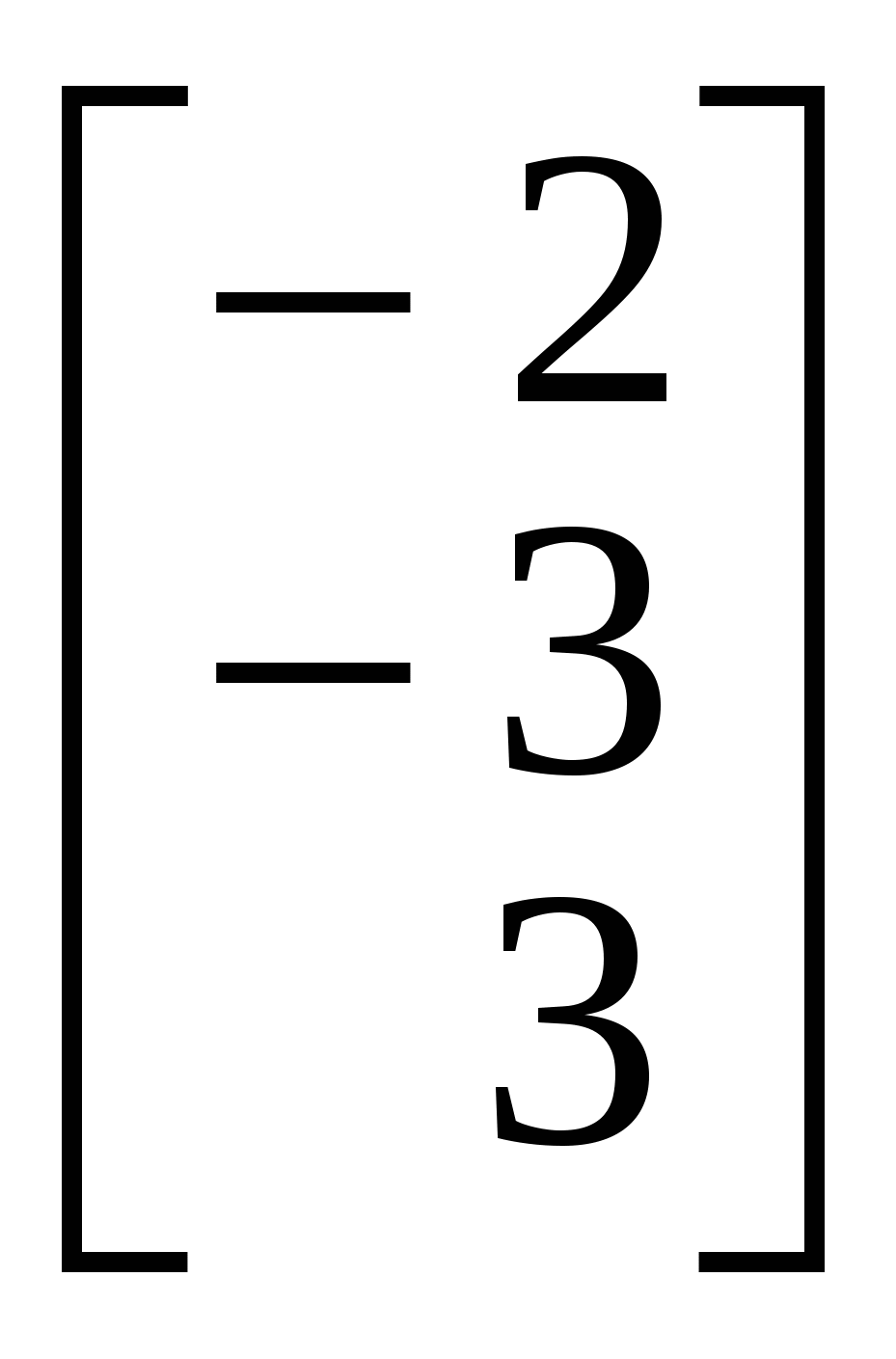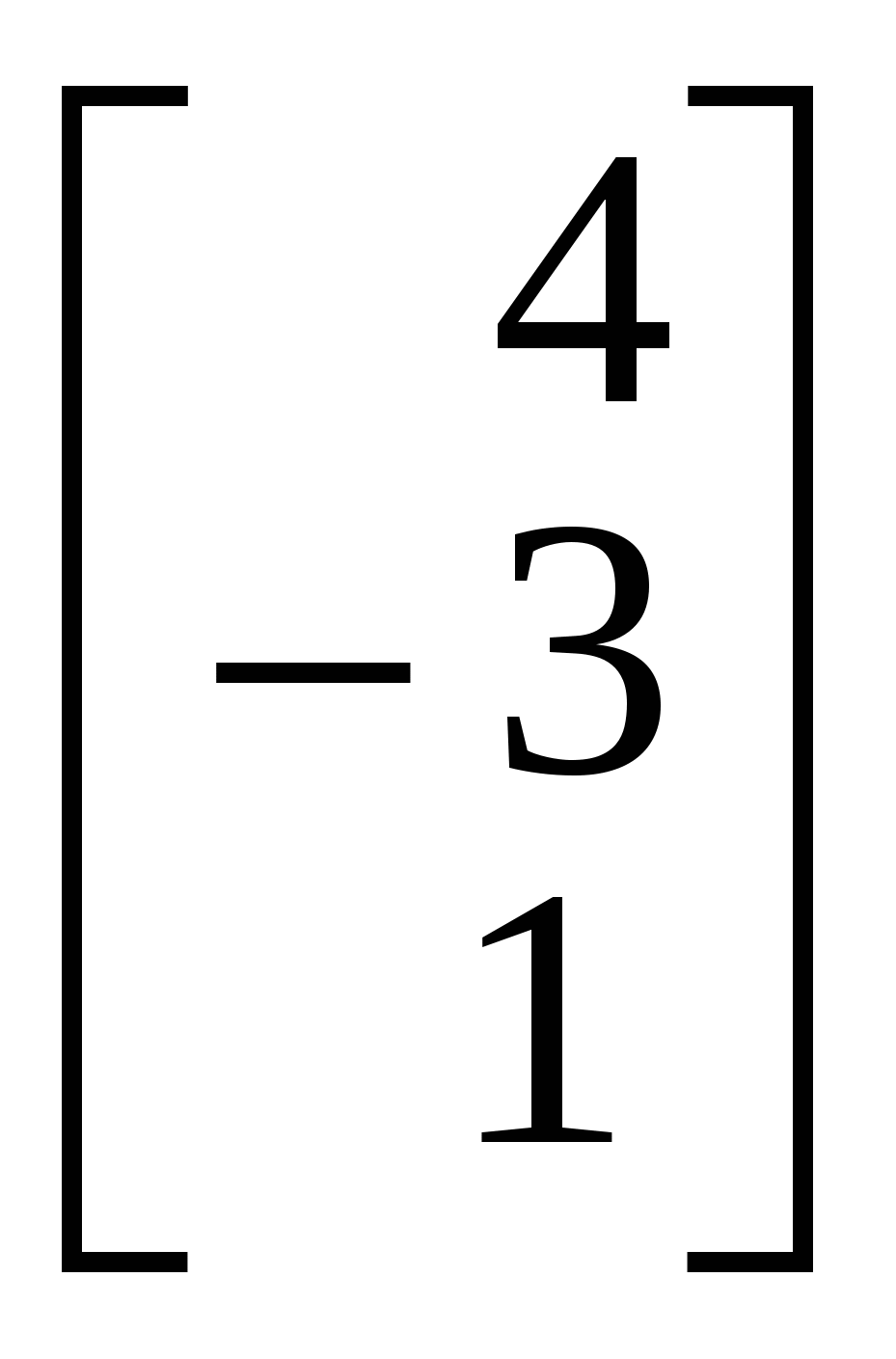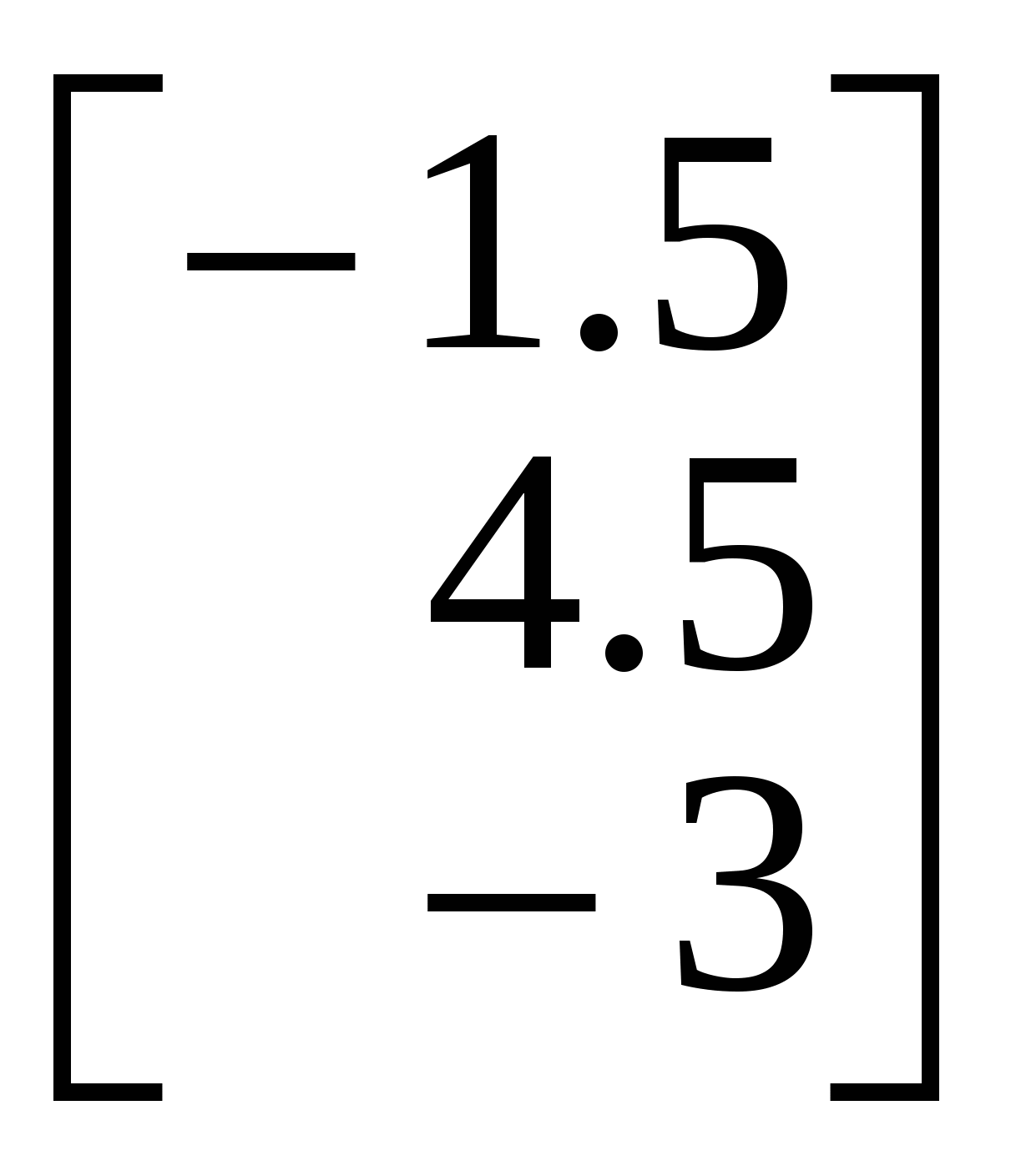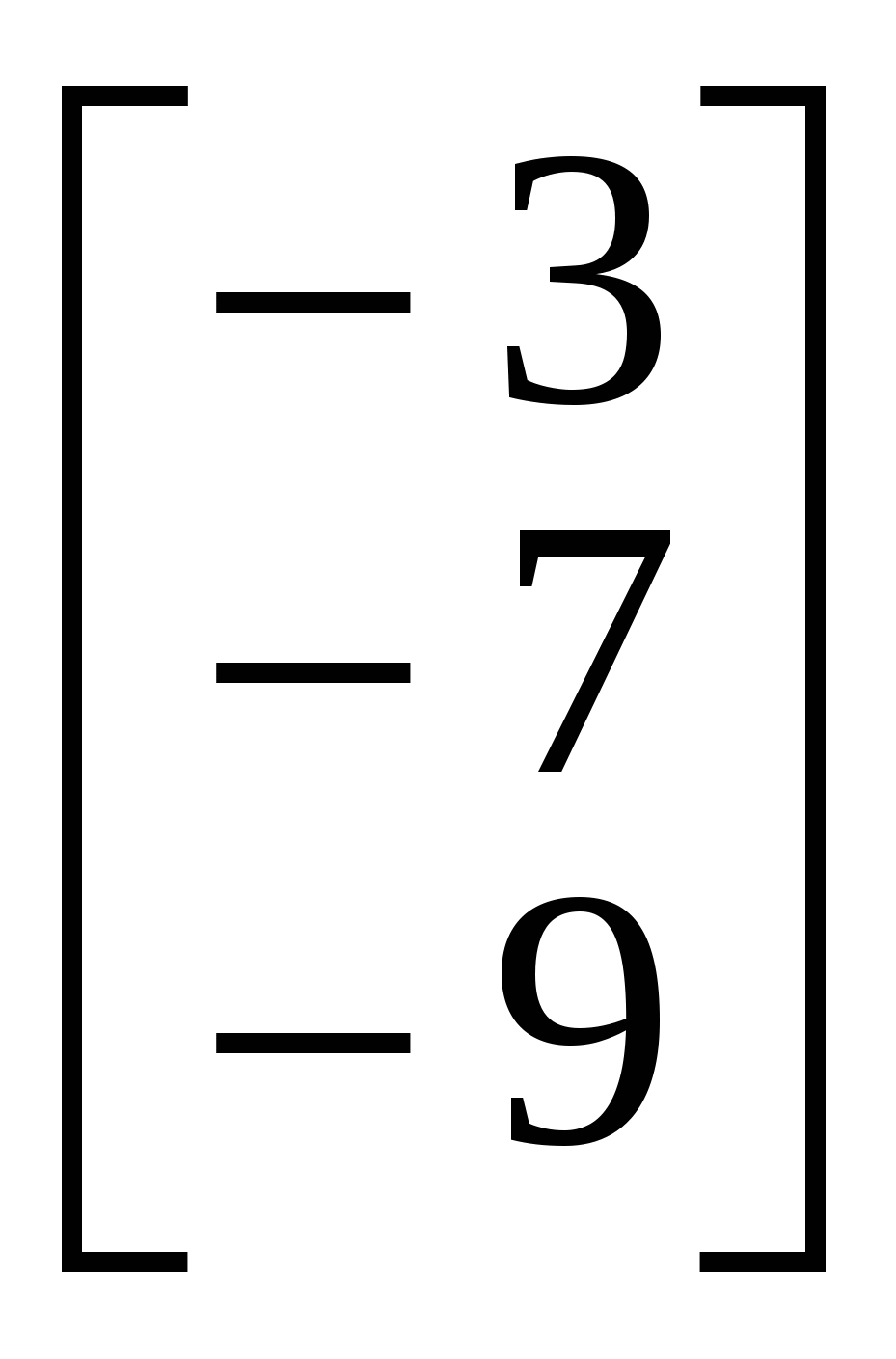и  :   ;   ;   ;  -1;   .3. Вычисление длины и направляющих косинусов вектора Длину и направляющие косинусы вектора можно найти исполь- зуя кнопки матричной и векторной палитры, калькулятора, палит- ры греческих букв, клавиатуры. Последовательность действий иллюстрирует следующий пример. ПРИМЕР 2.2 Введём вектор 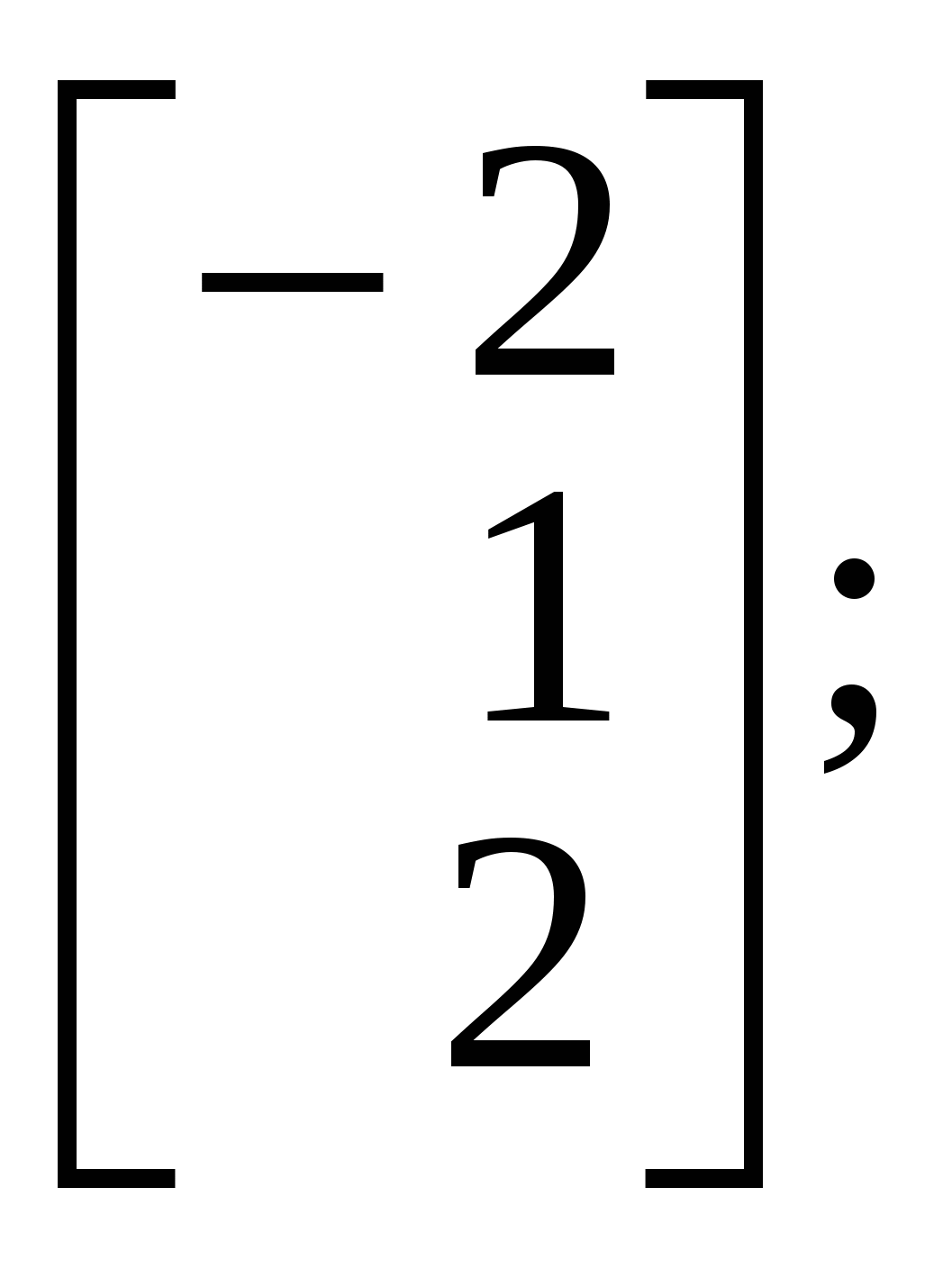и его координаты:   := -2;  := 1;  := 2.Найдём длину вектора и его направляющие косинусы:  cos : = cos : =  ; cos : =  ;Δ = 3; cos = -0.667; cos= 0.333; cos= 0.667. Направляющие косинусы вектора можно найти иначе, - умножая вектор 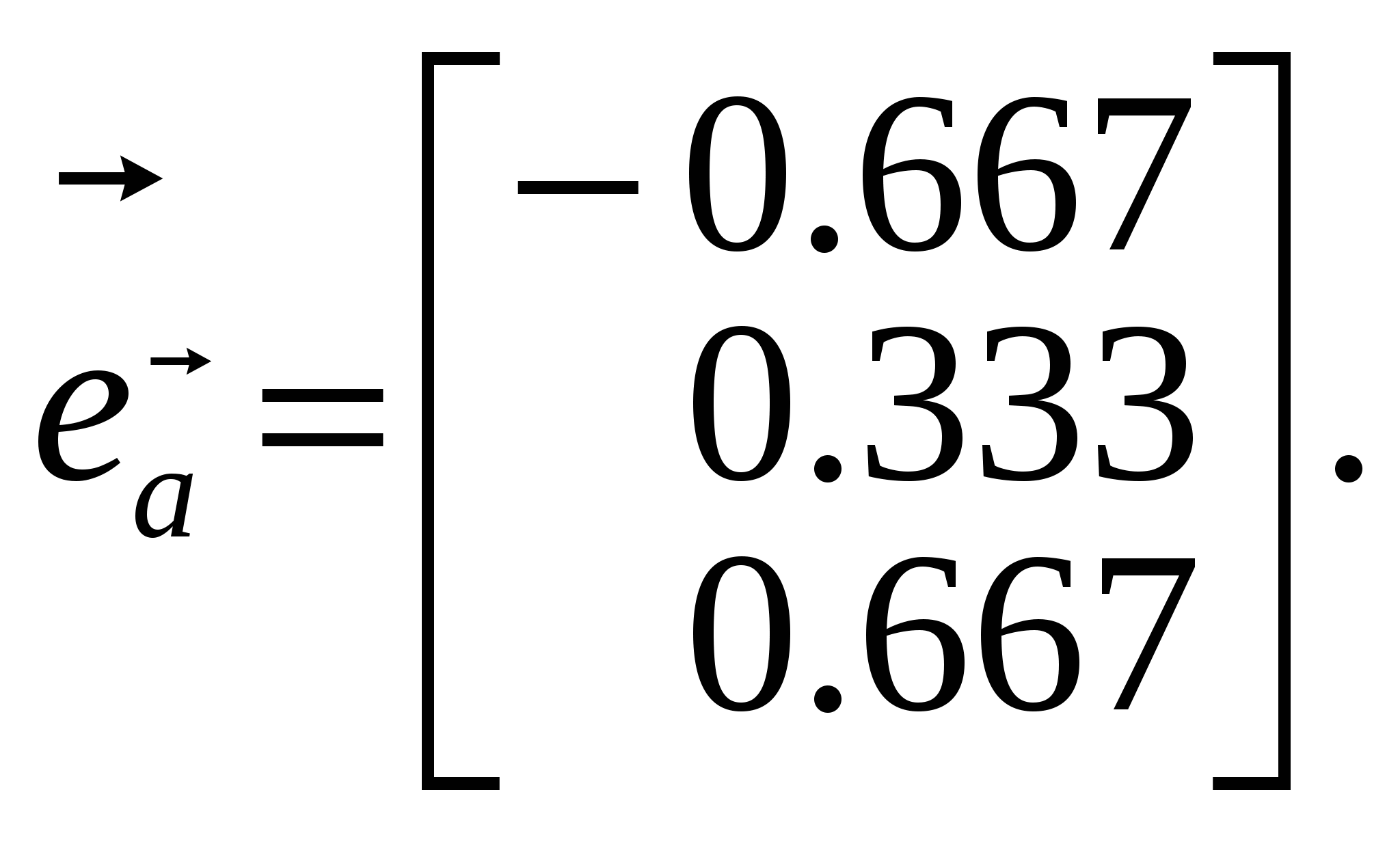на число  , т.е. найдя орт  вектора    4. Нахождение угла между векторами Рассмотрим следующий пример. ПРИМЕР 2.3 Введём векторы 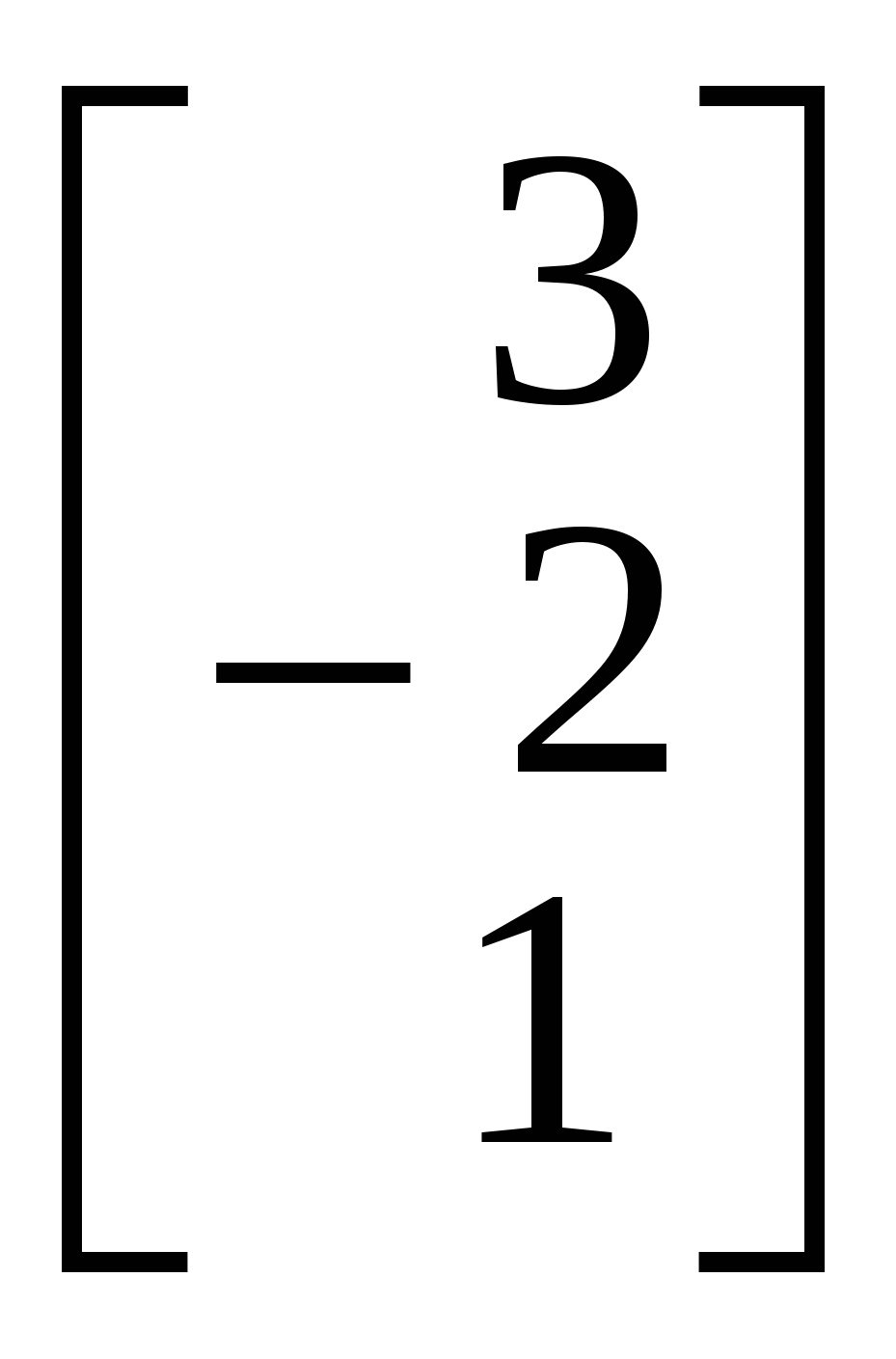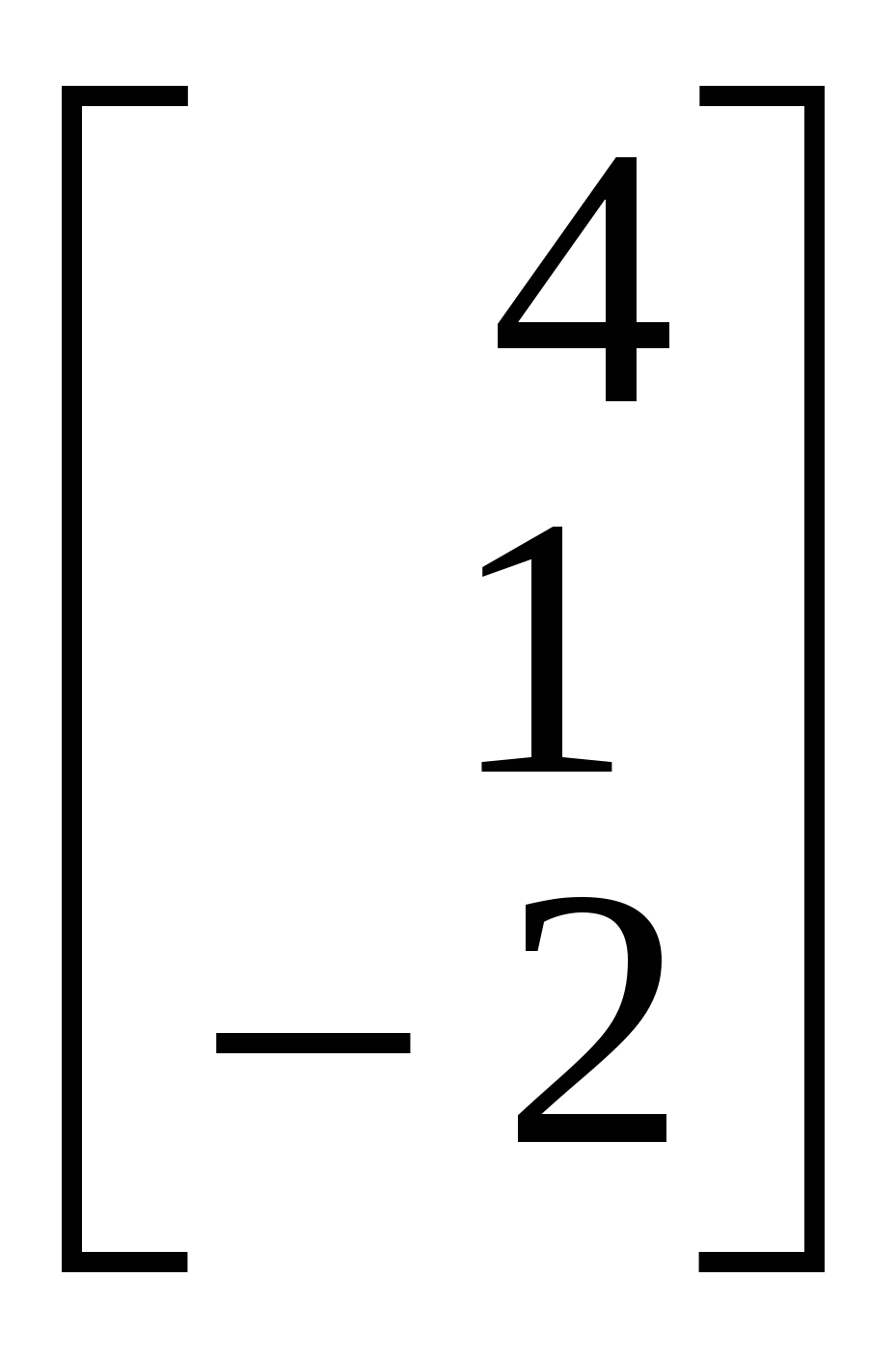и  : ;   .Найдём косинус угла  и угол между векторами  и  : ;   cos = 0.467; = 1.085 (рад.);  = 62.188˚. Чтобы вызвать функцию arccos нужно нажать клавишу  напанели инструментов и в открывшемся списке выбрать acos. 5. Составление уравнений Составление уравнений рассмотрим на примере нахождения уравнения плоскости проходящей через три заданные точки, не принадлежащие одной прямой. Пусть заданы точки А1(2;-1;3), А2(1;1;1), А3(- 4;0;3). Их радиус векторы 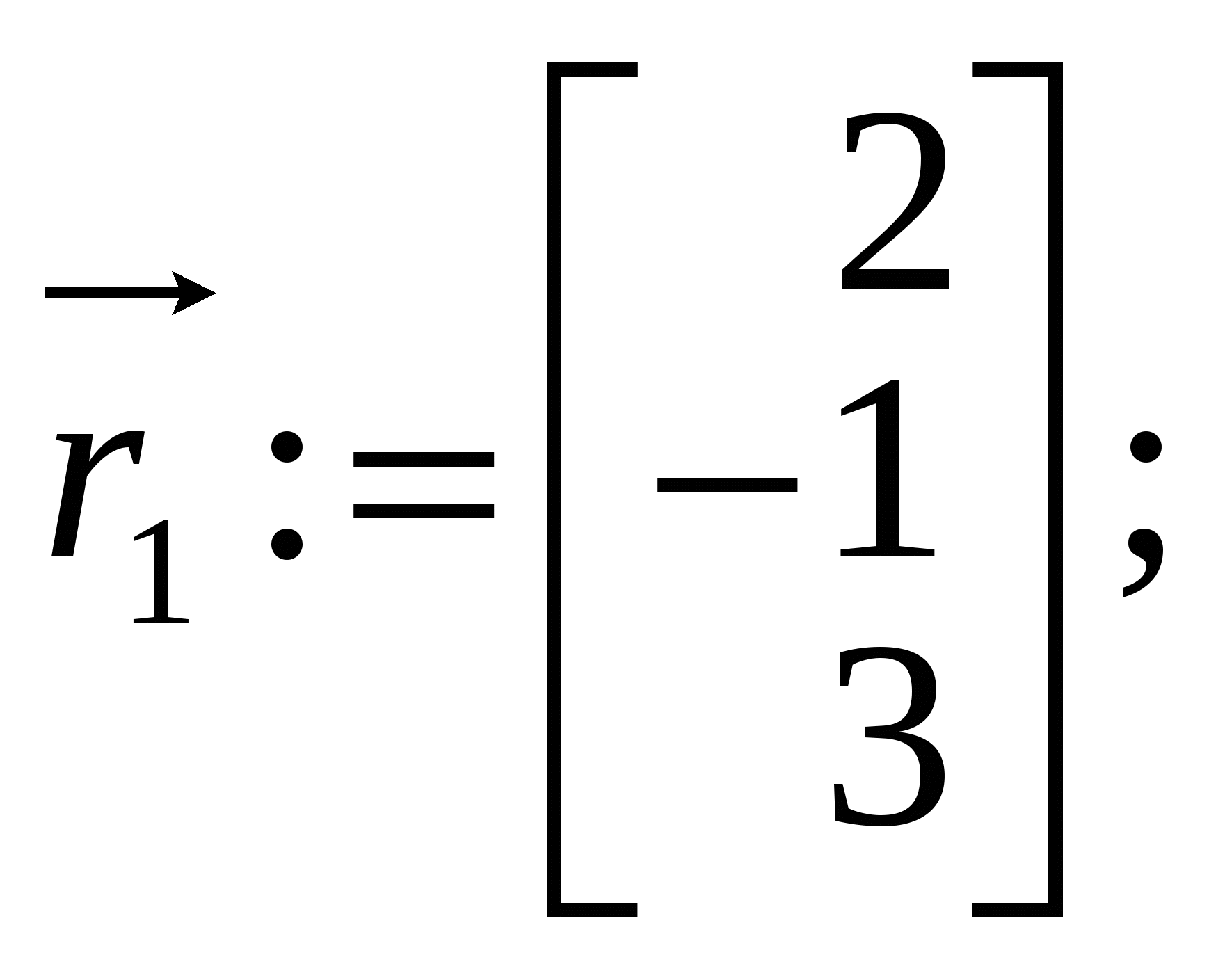 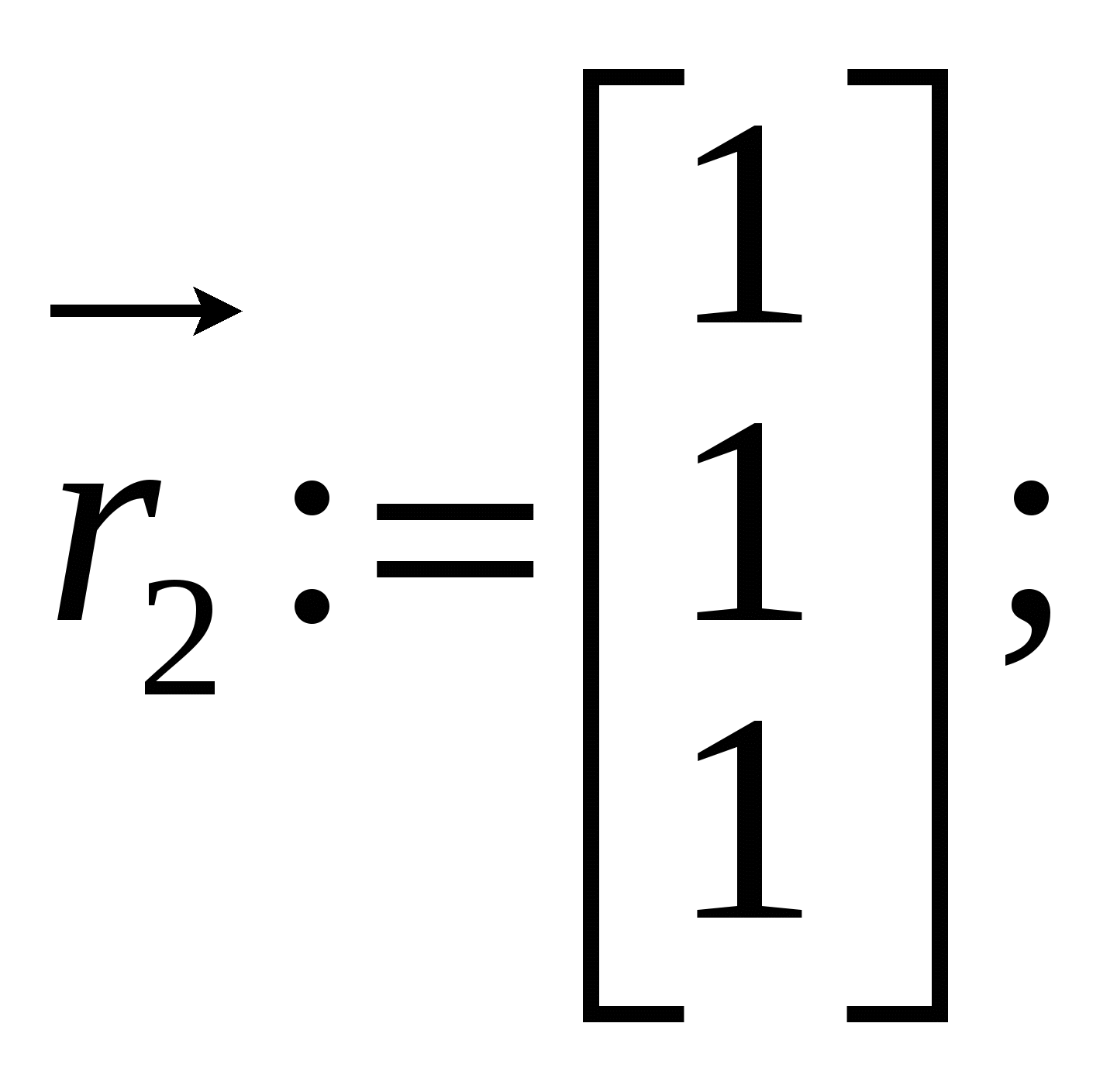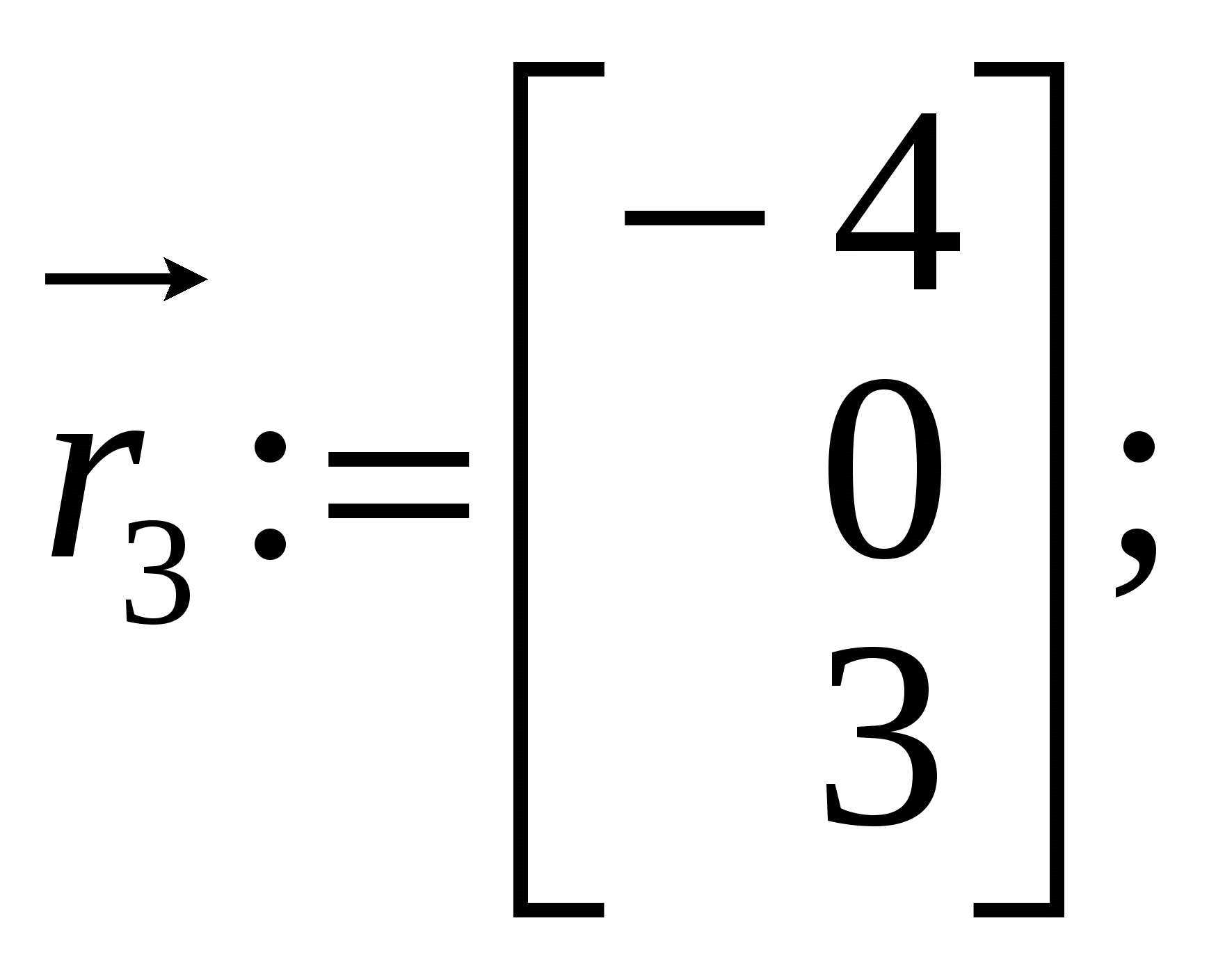, , имеют такие же координаты. Пусть  = ,  = . Тогда, вводя векторы     получим 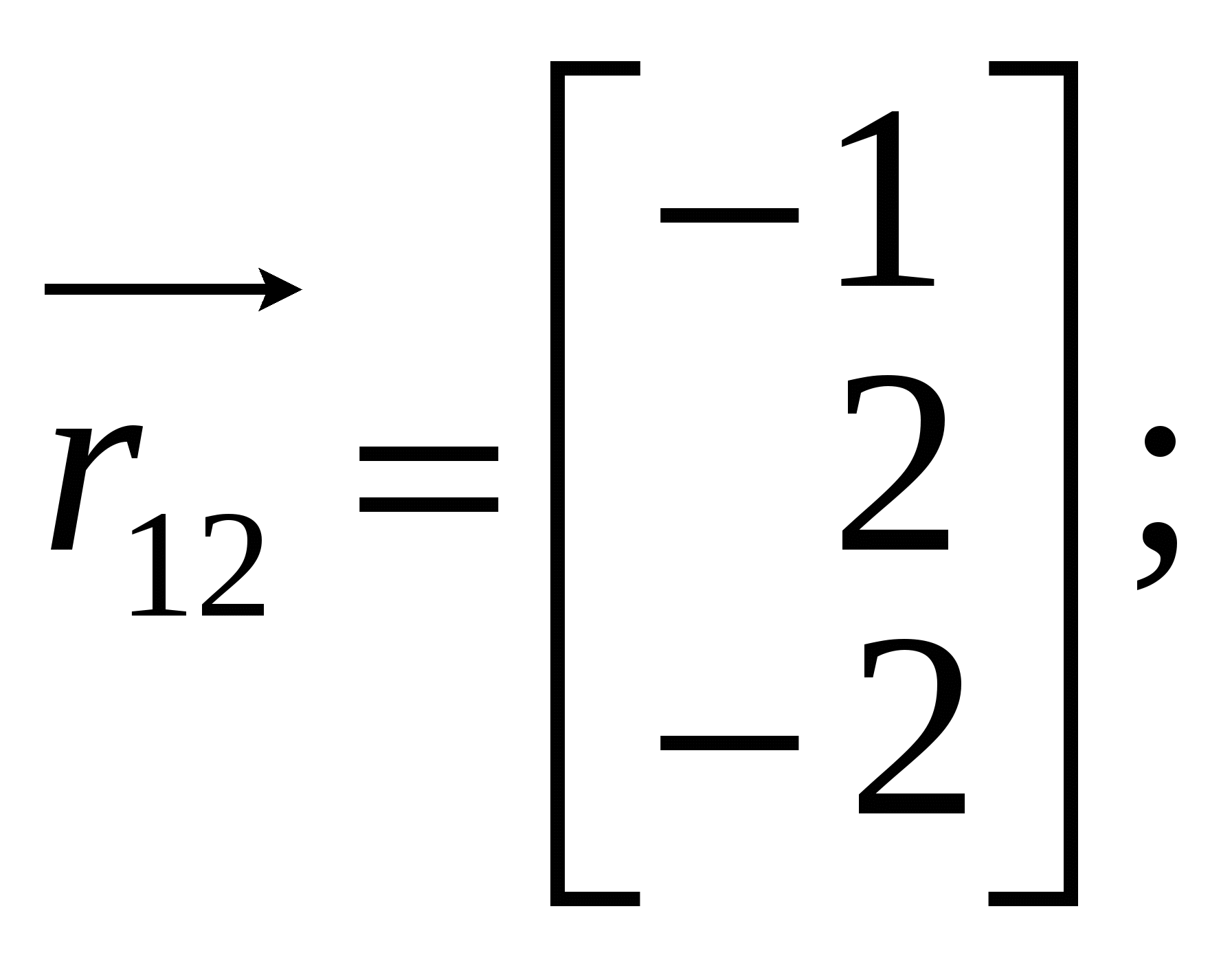 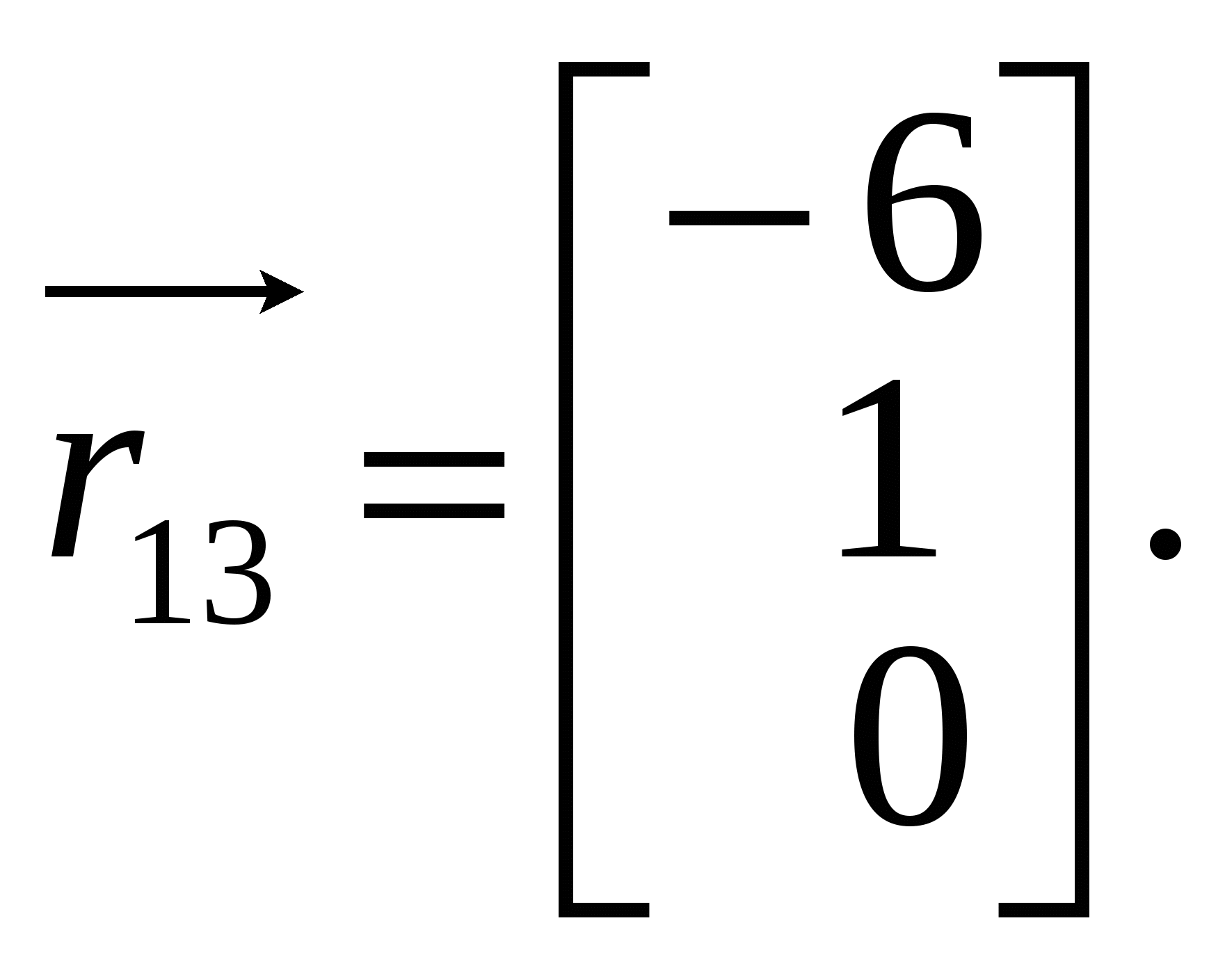 Убедимся, что точки А1,А2,А3 не принадлежат одной прямой. Действительно  = 6,  = 0.5,  = 0,и, следовательно, векторы и неколлинеарные.Уравнение плоскости А1А2А3 имеет вид 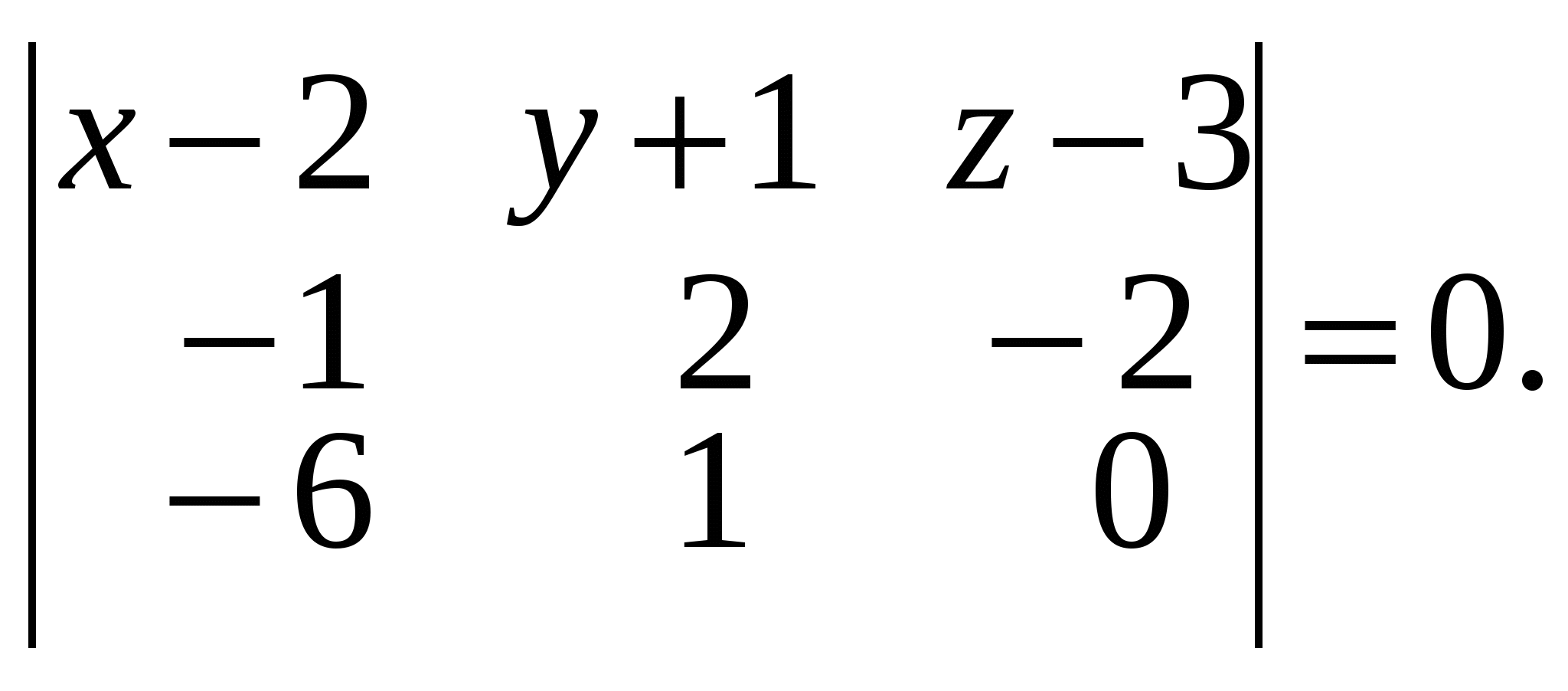 Раскроем определитель с помощью ЭВМ. Для этого нужно на- брать 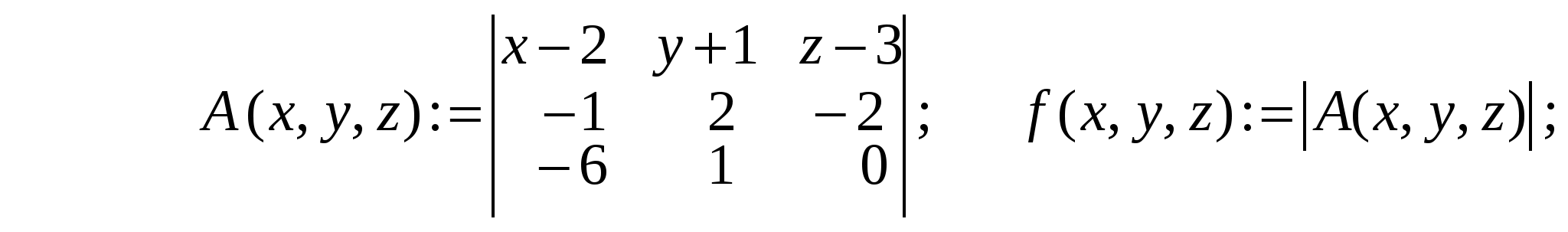  Итак, плоскость А1А2А3 имеет уравнение 2x + 12y + 11z - 25 = 0. 3. ОБРАЗЦЫ ВЫПОЛНЕНИЯ НЕКОТОРЫХ ЗАДАНИЙ Отчет к модулю системы "РИТМО" должен содеpжать титульный лист, содеpжание (отдельный лист), собственно отчет (несколько листов), библиогpафический список (отдельный лист). Все листы в отчёте должны быть пронумерованы (титульный лист считается первым листом отчёта, но номер на нем не ставит-ся; все остальные листы нумеруются: 2, 3, …). Тpебования, пpедъявляемые к офоpмлению отчета и отдельных его частей, пpиводятся на специальном стенде кафедpы высшей математики. Пpиведем pекомендуемую стpуктуpу отчета к модулю 2 "Векторная алгебра. Аналитическая геометpия" (соответствует уpовню сложности 2 и n=101, P30 = 11 и номер теоретического упражнения равен 12): Титульный лист Содеpжание
1.2. Пpактические упpажнения 1.2.1. Задание 1
1.2.3. Задание 3 1.2.4. Задание 4 1.2.5. Задание 5 1.2.6. Задание 6 1.2.7. Задание 7 1.2.8. Задание 8 1.2.9. Задание 9 1.2.10. Задание 11
3. Практическая часть 3.1. Решение теоpетического упpажнения 12
3.2.1. Решение задания 1
…………………………. 3.2.9. Решение задания 9 3.2.10. Решение задания 11 Библиогpафический список Рассмотpим pешения некотоpых пpактических упpажнений. Задание 1 Пусть n = 101. Тогда Р4 = 1 и номер задачи из табл. 1.1 равен 2. Груз весом  = 100кГ поддерживается двумя стержнями АВ иСВ. Определить силы (в кГ), возникающие в стержнях, если угол АСВ равен 90˚, угол АВС равен α = 3˚·([n/4] + 1). Если n = 101, то [n/4] = 25 и α = 78˚. Решение По условию груз поддерживается стержнями (находится в покое). Следовательно, вес груза - сила 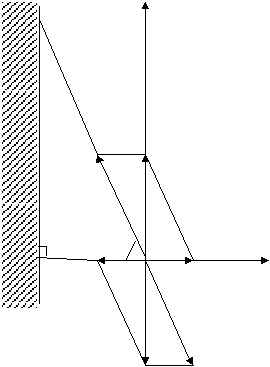 = (см. рис. 3.1) уравновешивается результирующей  сил, возникающих в стержнях под действием силы  , т.е.  (  и эти силы направлены противоположно). А у  N L C M1  B M x K N1 Рис. 3.1. Разложение веса груза по направлениям стержней Разложим силу  по направлениям стержней ВА и ВС. Для этого через точку L проведём прямые LM и LN, параллельные стержням ВА и ВС, до их пересечения с прямыми, содержащими стержни, в точках M и N. Очевидно, что Аналогично, раскладывается по направлениям стержней вес груза  и  Сила  вызывает растяжение стержня ВА и порождает силу , возникающую в этом стержне, уравновешивающую силу растяжения  Аналогично, сила  вызывает сжатие стержня ВС и порождает силу  , возникающую в стержне ВС, уравновешивающую силу сжатия .Найдём  и  обозначив    Введём декартову систему координат, как показано на рис. 3.1, и разложим векторы  и  по базису  этой системы координат.Очевидно, что    Поскольку груз находится в покое, то результирующая этих сил равна нулевому вектору  , т.е.   Это векторное равенство равносильно системе двух (скалярных) уравнений  откуда получаем  Эти формулы можно получить и иначе. Треугольник BML прямоугольный, ВМ = а, BL = P, ML = b, угол BML равен , и  откуда  Учитывая условия задачи получим  |