Основы технической механики. Методические указания к контрольной работе Задачи алгоритм и пример решения Исходные данные () 23 Схемы к задачам 130

• Название: Методические указания к контрольной работе Задачи алгоритм и пример решения Исходные данные () 23 Схемы к задачам 130
• Анкор: Основы технической механики .doc
• Дата: 24.04.2017
• Размер: 2.8 Mb.
• Имя файла: Основы технической механики .doc
• Тип: Методические указания; #4563
• страница: 5 из 8

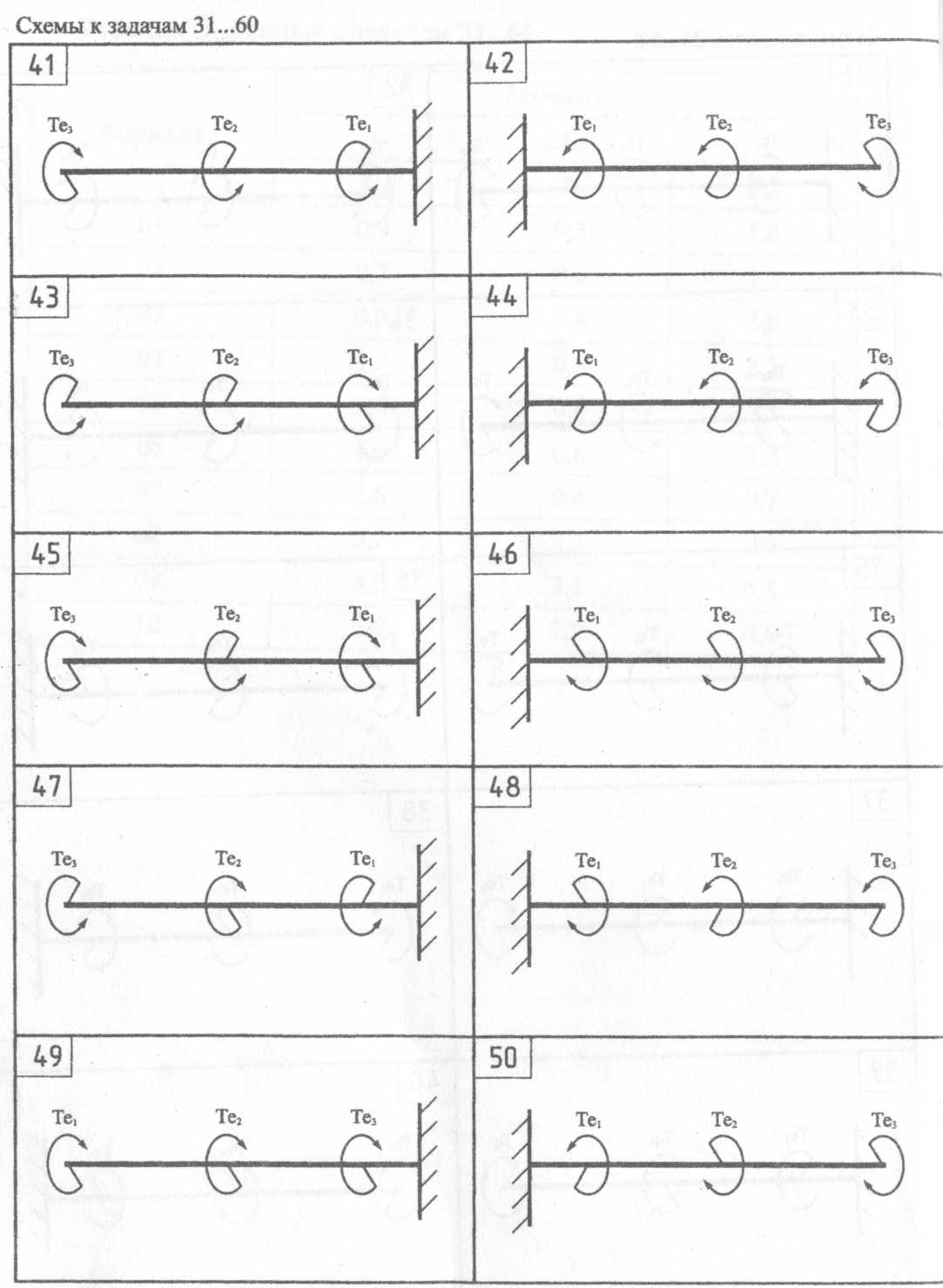
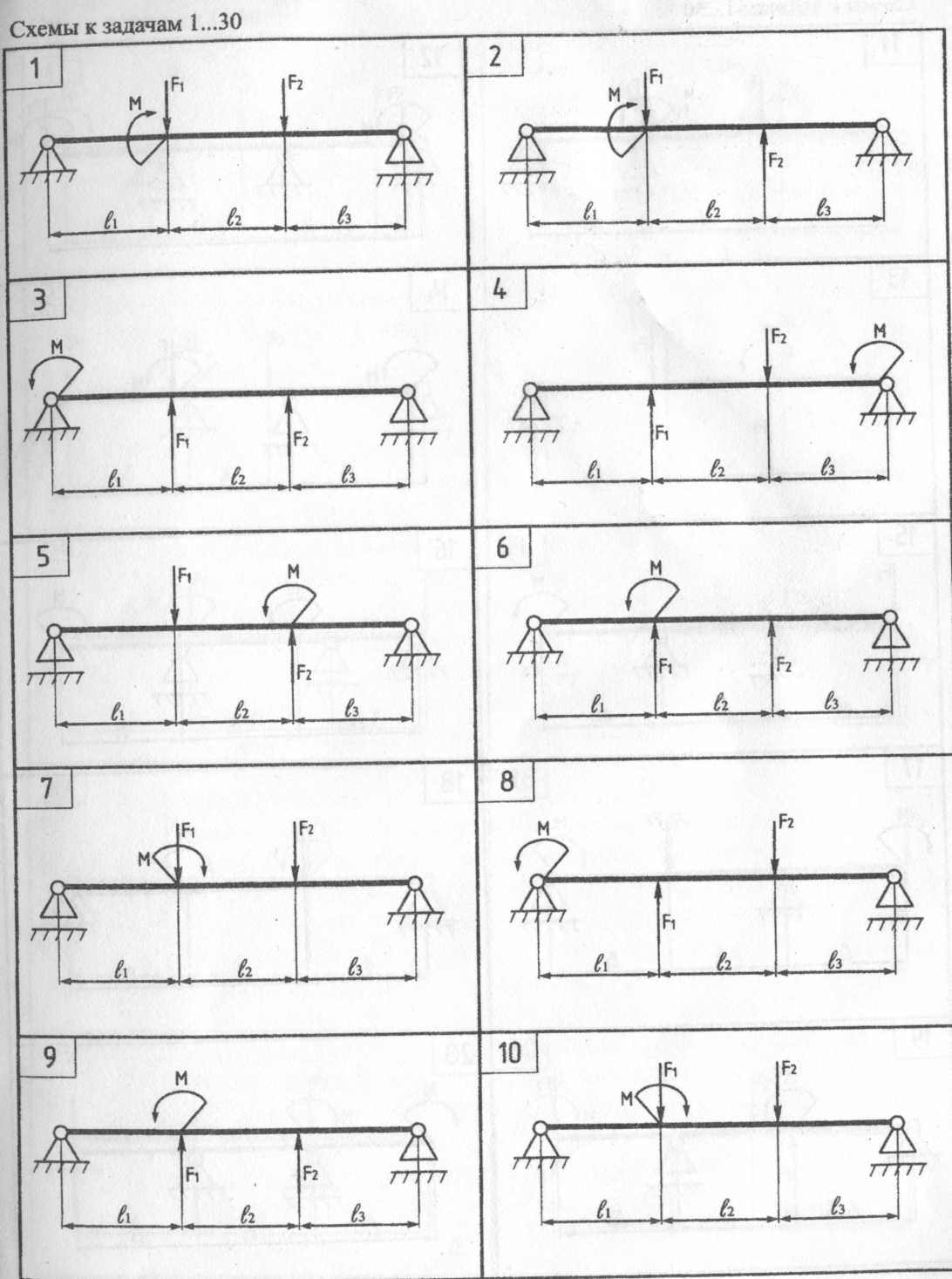Задачи 31...60
Для заданного бруса построить эпюру крутящих моментов и подобрать размеры сечения в двух вариантах: а) круг; б) кольцо с заданным отношением C = d₀/d = 0,75 внутреннего и наружного диаметров. Сравнить массы брусьев по обоим расчетным вариантам. Указанные расчеты выполнить только для участка с опасным сечением. Ответить на вопрос: во сколько раз большую нагрузку на брус можно допустить при увеличении размера сечения в 2 раза? Во сколько раз возрастут при этом затраты материала? Для материала бруса (Сталь Ст5) принять допускаемое напряжение кручения [τ] =100 МП*
Алгоритм решения задач 31...60

1. 
   Изображаем брус со всеми приложенными к нему скручивающими моментами Т_е1, Т_е2,Т_е3.
   
2. 
   Для построения эпюры крутящих моментов делим брус на участки I, II, III, начиная со свободного конца, и, применяя метод сечений, находим значение крутящего момента на каждом участке. По найденным значениям T строим эпюру крутящих моментов.
   
3. 
   Определим размеры поперечного сечения бруса для участка бруса с наибольшим по абсолютной величине крутящим моментом в двух вариантах. Для этого используем условие прочности при кручении
   

τ =T/Wp≤[τ],

где полярный момент сопротивления Wp является геометрической характеристикой прочности поперечного сечения и для круга диаметром dвыражается формулой Wp = nd³/16 = 0,2d³; для кольца Wp = πd³(1-С⁴)/16 = 0,2d³(l-C⁴). Значение диаметров dи d₀ округляем до конструктивного значения (то есть четное число, либо оканчивающееся на 0 или 5).

4Сравним затраты материала по обоим расчетным вариантам. Отношение масс брусьев одинаковой длины равно отношению площадей их сечений. Площадь круглого сечения A_кр =πd²/4; площадь кольцевого сечения А_кол= πd² (1-С²)/4.

Тогда т_кр/т_кол = А_кр/A_кол
Пример 2. Для бруса построить эпюру крутящих моментов и подобрать размеры сечения в двух вариантах: а) круг; б) кольцо с заданным отношением С=d₀/d=0,75 внутреннего и наружного диаметров. Сравнить массы брусьев. Принять допускаемое напряжение [τ] = 100 МПа.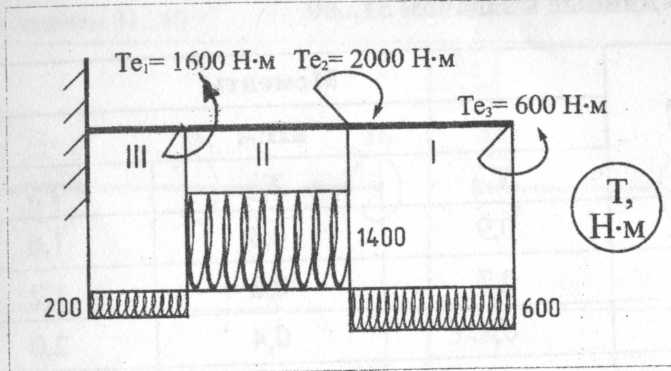


Решение:

1 Изображаем брус и показываем приложенные скручивающие моменты в Н·м.

2. 
   Делим брус на участки I, II, III, начиная со свободного конца; границами участков являются сечения, в которых приложены внешние скручивающие моменты Т_е1, Т_е2,Т_е3.
   
3. 
   Определяем величину внутренних крутящих моментов в сечениях на каждом из участков бруса:
   

Т₁=-Т_е3=-600Н·м;

Т₂ = -Т_е3+Т_е2 = -600+2000 =-1400 Нм;

Т₃ = -Т_е3+Т_е2-Т_е1= -600+2000-1600 = -200 Н·м

Строим эпюру Г (в масштабе). Отрицательные значения моментов откладываем вниз от оси эпюры.

4Для опасного участка II определяем размеры поперечного сечения бруса. Используем условие прочности при кручении

t₂ = T₂/W_p2≤[τ];

τ =1400·10³/W_p2= 100, отсюда требуемый W_p2= 14·10³ мм³.

Для круглого сечения приравниваем 0,2d₂³ = 14·10 мм³ и находим d₂ = =41,2 мм. Принимаем d₂ = 42 мм.

Для кольцевого сечения (С = 0,75) принимаем: 0,2d₂³(l-0,75⁴) = 14·10³ мм³и находим d₂=48 мм. Тогда d_o2 = 0,75·48 = 36 мм.

Теперь сравним затраты материала по обоим расчетным вариантам. Отношение масс брусьев одинаковой длины равно отношению площадей их сечений.

Площадь круглого сечения А_кр=πd₂²/4 = 3,14·42² /4 = 1385 мм² .

Площадь кольцевого сечения А_кол= 3,14(48² -36² )/4 = 791мм .

Тогда т_кр/т_кол=A_кр/A_кол=1385/791=1,8

Следовательно, брус круглого сечения тяжелее бруса кольцевого сечения примерно в 2 раза.


Таблица 3 – Данные к задачам 31…60

Вариант	Моменты
	кН-м
	Tel	Та	Те3
01	0,9	0,3	1,6
02	0,7	0,8	1,2
03	0,8	0,4	2,0
04	1,2	0,5	2,5
05	1,0	0,8	2,1
06	1,0	0,6	3,2
07	2,6	0,4	0,7
08	2,2	2,3	0,9
09	3,0	2,1	0,8
10	5,0	2,2	0,6

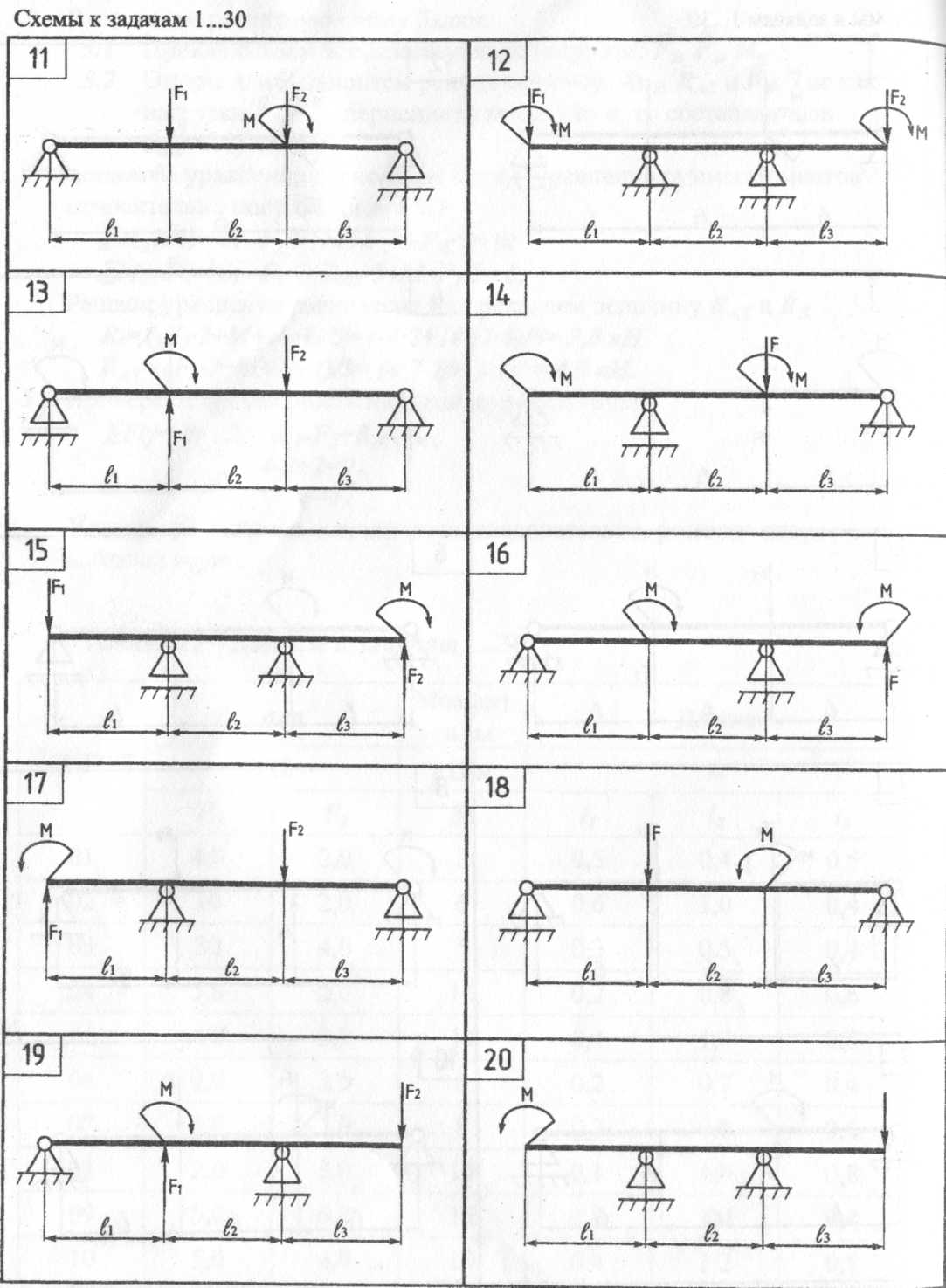
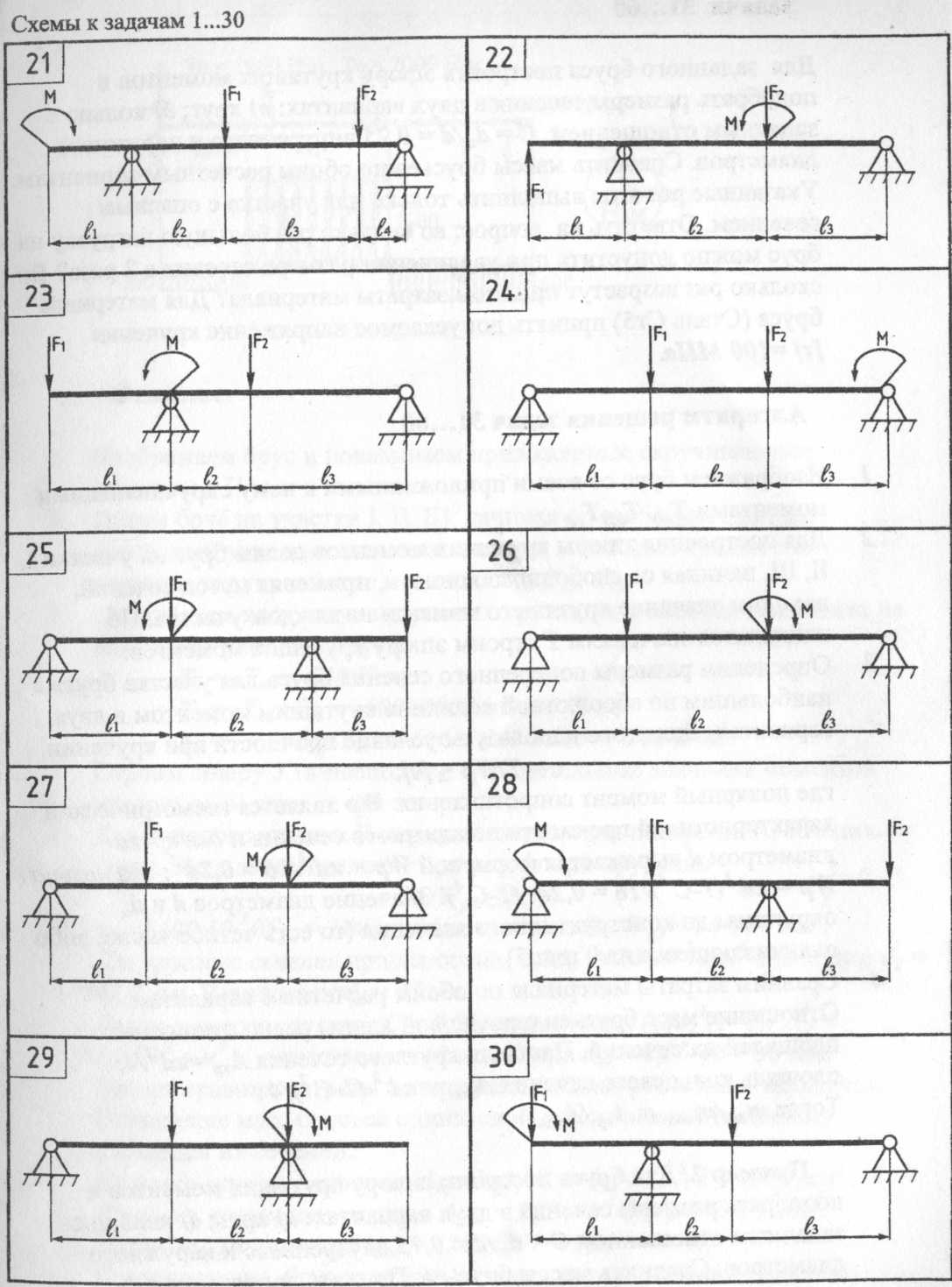
Задачи 61...90
Для заданной балки построить эпюры изгибающих моментов.

Для опасного сечения определить из расчета на прочность требуемый момент сопротивления поперечного сечения балки, принимая допускаемое напряжение [σ]=160 Мпа.

Подобрать по таблицам ГОСТ 8239-89 и ГОСТ 8240-37 соответствующие требуемому моменту сопротивления номера профилей прокатной стали в двух вариантах:

а) балка двутавровая;

б) балка состоит из двух рядом поставленных швеллеров.

Найти отношение массы балки, состоящей из двух швеллеров к массе двутавровой балки.
Алгоритм решения задач 61...90
1 Вычертить балку, указав величину и направление нагрузок (F, М), а также длины участков.

2. 
   Изобразить оси координат у и z, направив г по оси балки, а ось у перпендикулярно ей.
   
3. 
   Освободить балку от опор, заменив их опорными реакциями.
   
4. 
   Составить два уравнения равновесия, выбрав в качестве центров моментов точки опор балки:
   

ΣM_A(Fi) = 0;

ΣM_B(Fi) = 0.

5Составить проверочное уравнения равновесия:

ΣFiy = 0.

Если реакция опоры получается отрицательной, следует перечеркнуть предварительно выбранное направление и показать новое направление. Найденные значения реакций опор проставить на чертеже.

6. 
   Определить величину изгибающих моментов в характерных сечениях балки, применяя метод сечений.
   
7. 
   Построить эпюру изгибающих моментов. Если максимальный изгибающий момент получается со знаком минус, то знак минус опускаем, так как при расчете на прочность он не имеет значения.
   

8 Из условия прочности балки при изгибе определяем размеры ее поперечного сечения σ = \М_тах\/W_x≤ [σ];

W_x≥\М_тах\/[σ];

9 Находим отношение масс балок, равное отношению их площадей.