Основы технической механики. Методические указания к контрольной работе Задачи алгоритм и пример решения Исходные данные () 23 Схемы к задачам 130
 Скачать 2.8 Mb. Скачать 2.8 Mb.
|
|
К теме 2.6 Изгибы 38 Как следует нагрузить брус, чтобы возник: а) чистый прямой изгиб? б) поперечный прямой изгиб?
К теме 2.7 Изгиб с кручением
К теме 2.8 Устойчивость сжатых стержней
К теме 2.9 Расчет на прочность при переменных напряжениях
К темам 3.1, 3.2 Основные понятия кинематики. Кинематика точки
а) аn = 0 и аτ= 0; б) аn = 0 и аτ ≠ 0; в) аn≠0 и aτ = 0; г) аn. ≠ 0 и аτ ≠ 0. К теме 3.3 Простейшие движения твердого тела
10 Определите угловую скорость вращения Земли вокруг своей оси? К теме 3.4 Основные понятия и аксиомы динамики
К теме 3.5 Силы инерции. Метод кинетостатики
К теме 4.1 Основные понятия и определения 1 Что представляет собой кинематическая пара? Приведите примеры кинематических пар. 2 Что называется механизмом? Приведите примеры механизмов, получивших наибольшее распространение. К теме 4.2 Соединения деталей
К теме 4.3 Механизмы поступательного, колебательного и прерывистого движения
К теме 4.4 Винтовые механизмы
К теме 4.5 Механизмы передач и вращательного движения
К темам 4.6 ,4.7 Валы и оси. Направляющие вращательного движения
К теме 4.8 Муфты
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ К задачам 1...30. К решению этих задач следует приступать после изучения тем: «Основные понятия и аксиомы статики», «Плоская система сходящихся сил», «Пара сил», «Плоская система произвольно расположенных сил», уяснения приведенных ниже указаний и рассмотрения примеров. Во всех задачах определению подлежат реакции опор тела (балки), находящегося в равновесии под действием плоской системы произвольно расположенных сил. Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. Твердое тело называется несвободным, если его перемещение в пространстве ограничено какими-либо телами. Все тела, которые, так или иначе, ограничивают перемещение данного тела, называют его связями. В природе нет абсолютного покоя, и тела, стремясь перемещаться в пространстве под действием сил, сами действуют на препятствующие этому перемещению связи, вызывая в них равные по модулю, но противоположно направленные реакции связей. В разделах «Статика» и «Сопротивление материалов» рассматривают состояние равновесия несвободных тел, опирающихся на неподвижные опоры или закрепленных в определенных точках. Возникающие в этих случаях реакции связей называют опорными реакциями или реакциями опор. В плоских конструкциях (балках, рамах и т.д.) встречаются три основных типа опор:
Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Если пренебречь трением на опоре и в шарнире, то реакция такой связи будет направлена перпендикулярно опорной плоскости и неизвестна только по модулю (одна неизвестная). Шарнирно-неподвижная опора допускает только поворот вокруг оси шарнира, и не допускает ни каких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира; модуль и направление ее заранее неизвестны (две неизвестные). При решении задач такую опору заменяют двумя взаимно перпендикулярными составляющими. Жесткая заделка не допускает ни линейных, ни угловых перемещений. Эту опору заменяют двумя взаимно перпендикулярными составляющими и реактивным моментом (три неизвестные). 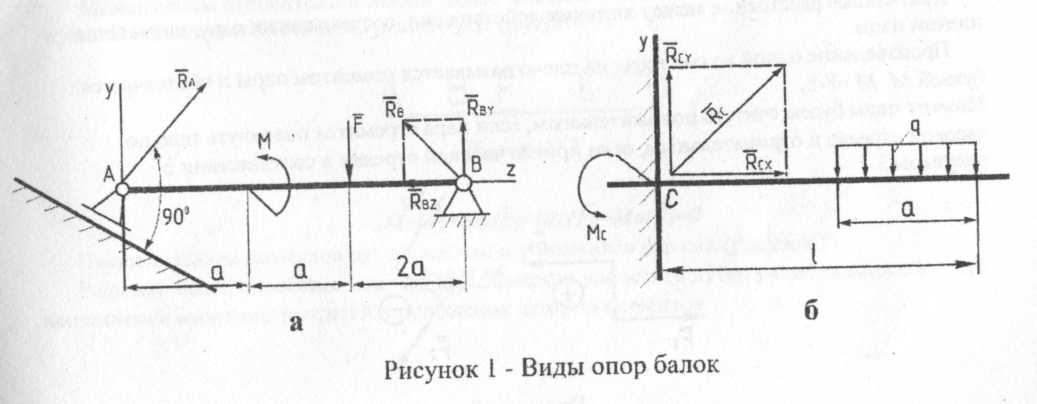 Для балок, имеющих две опоры, рекомендуется определять реакции, используя уравнения равновесия плоской системы произвольно расположенных сил (рисунок 1а). 1. ΣМа(Ḟi) = 0; =>Rby; 2. ΣМв(Ḟi) = 0; =>Ra; 3. ΣFiy= 0 ; =>Rbz ; Уравнение ΣFiy= 0 используется для контроля. Если при решении задачи реактивная сила получается отрицательной, то ее направление противоположно принятому. «Пара сил» Система двух равных и параллельных сил, направленных в противоположные стороны и не лежащих на одной прямой, называется парой сил или просто парой в соответствии с рисунком 2. 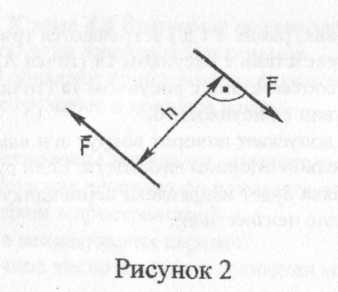 Кратчайшее расстояние между линиями действия сил, составляющих пару называется плечом пары. Произведение одной из сил пары на плечо называется моментом пары и обозначается буквой М: M=F·h. Момент пары будем считать положительным, если пара стремится повернуть тело по часовой стрелке и отрицательным, если против часовой стрелки в соответствии с рисунком 3. 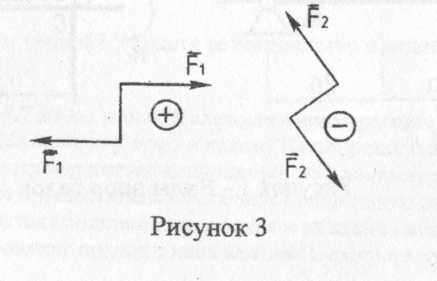 Это правило является условным. Размерность пары (Нм, кНм). Чтобы задать пару, достаточно задать ее момент, поэтому, слово «пара» заменяют, словом «момент» и условно изображают его так, как показано на рисунке 4. 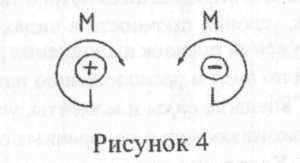 Необходимо помнить свойства пары сил:
Момент силы относительно точки. Моментом силы относительно точки называется произведение силы на длину перпендикуляра, опущенного из этой точки на линию действия силы. В соответствии с рисунком 5 точка О, относительно которой берется момент, называется центром момента. h– плечо силы относительно точки О. Момент силы F-относительно точки О будет равен: Mo(Ḟ)=F·h 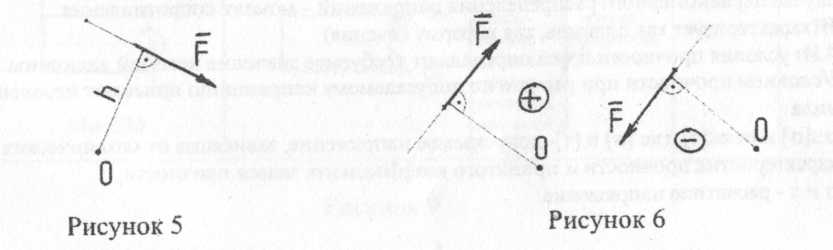 Момент силы относительно любой точки, лежащей на линии действия этой силы, равен нулю, В этом случае плечо силы равно нулю (рисунок 7).  Ma(F)=Mb(F)=Mc(F)=Md(F)=0 Правило знаков моментов сил то же, что и у моментов пар сил (рисунок 6). Решение задач, подобных задачам 1…30, 61…90, можно упростить путем рационального выбора направления координатных осей и положения центров моментов. К задачам 31...60. Приступая к решению задач 31...60 и 61...90, в которых выполняются расчеты деталей и конструкций на прочность, прежде всего, необходимо повторить из раздела «Статика» методику определения реакций связей стержневых конструкций и балок. Затем, изучив соответствующий материал, получить четкое представление о методе сечений для определения внутренних силовых факторов, видах нагружения бруса, напряжениях, условии прочности и видах расчетов на прочность. Общий для всех видов нагружения порядок выполнения расчета на прочность:
З.По виду ВСФ устанавливают вид напряжени^возникающего в точках опасного поперечного сечения, закон его распределения по сечению и вид геометрической характеристики прочности сечения (ГХП) Расчетное напряжение (максимальное напряжение в опасной точке опасного сечения бруса) определяют как отношение ВСФ/ГХП. В случае равномерного распределения напряжений по поперечному сечению в качестве ГХП применяется площадь сечения А (форма сечения значения не имеет), в случае неравномерного распределения напряжений - момент сопротивления W (характеризует как площадь, так и форму сечения). 4.Из условия прочности бруса определяют требуемое значение искомой величины. Условием прочности при расчете по допускаемому напряжению называют неравенство вида σ≤[σ] или τ≤[τ], где [σ] и [τ] – допустимое напряжение, зависящее от механических характерис ΣFiy= 0 тик прочности и принятого коэффициента запаса прочности; σ и τ – расчетное напряжение.
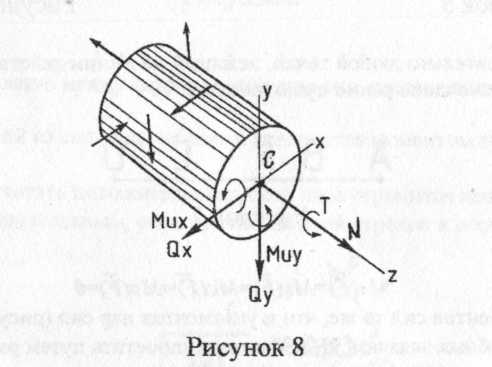
Виды ВСФ N – продольная сила; Q – поперечная сила? Ми – изгибающий момент; Т – крутящий момент (рисунок 8) 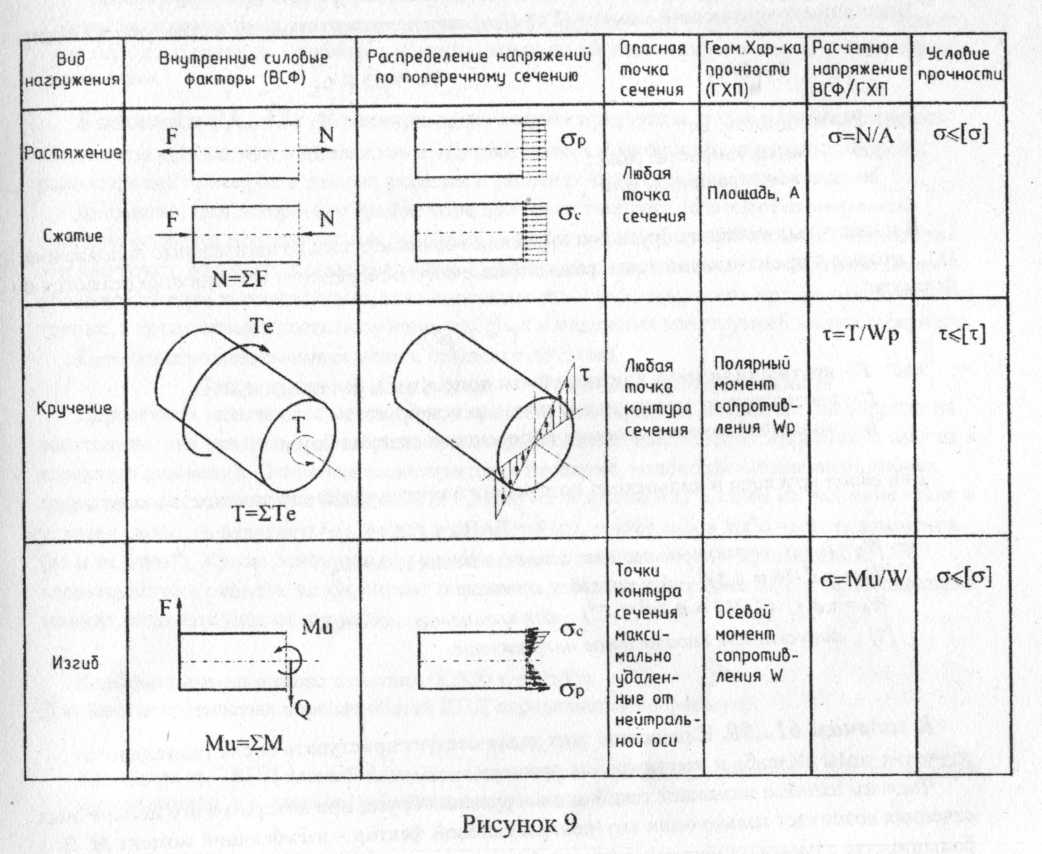 При рассмотрении любой из оставленных частей бруса со стороны смещения, внешние моменты. Те, действующие по ходу часовой стрелки, считаем положительными, действующие против хода часовой стрелки – отрицательными. Знак крутящего момента, физического смысла не имеет.  * Torsion (англ.) - кручение ** Индекс е от external (англ.) - внешний Внешний скручивающий момент (Те* Нм)определяется по одной из следующих формул: Te=Р/ω; Те=9,55 Р/n, где: Р–мощность, Вт; ω – угловая скорость, рад/с; n – частота вращения, мин-1 В поперечных сечениях бруса при кручении возникают только касательные напряжения (т), которые в произвольной точке рассматриваемого поперечного сечения определяются по формуле: τ=T·p/jp, где: Т – крутящий момент в исследуемом поперечном сечении; Р – расстояние от исследуемой точки до оси бруса; jp – полярный момент инерции поперечного сечения бруса. Для валов круглого и кольцевого поперечного сечения условие прочности имеет вид: где:Wp=jp / р – полярный момент сопротивления сечения; Wp = πd3/16 = 0,2d3 – для круглого сечения; WP= πd3(1-С4)/16 =0,2 πd3(1-С4) –для кольцевого сечения; [τ] – допускаемое касательное напряжение. К задачам 67... 90. К решению этих задач следует приступать после тщательного изучения темы «Изгиб» и рассмотрения примера. Чистым изгибом называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор изгибающий момент М.В большинстве случаев одновременно с изгибающим моментом возникает и другой внутренний силовой фактор - поперечная сила Q; такой изгиб называют поперечным. Изгибающий момент в поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на оставленную часть, относительно центра тяжести сечения: Mz=ΣМ- Имеется в виду, что все внешние силы и моменты действуют в главной продольной плоскости бруса, причем силы расположены перпендикулярно продольной оси. При чистом изгибе в поперечных сечениях возникают нормальные напряжения а,а при поперечном изгибе, кроме того, и касательное напряжение т. Однако в подавляющем большинстве случаев влияние х при расчете на прочность не учитывается, поэтому отпадает необходимость как в определении поперечных сил Q, так и в построении их эпюры. Правило знаков для изгибающего момента следующее: момент внешней силы или пары, изгибающий мысленно закрепленную в сечении оставленную часть бруса выпуклостью вниз, считается положительным, в противном случае – отрицательным. 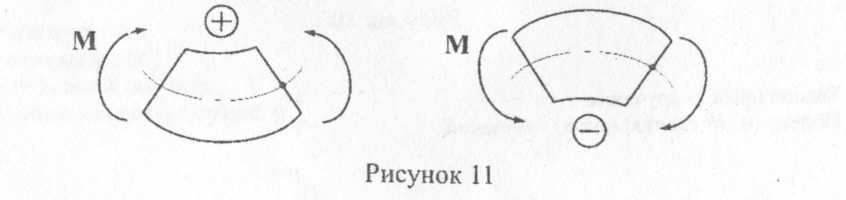 Для двухопорной балки решение следует начинать с определения опорных реакций. Балки выполняют постоянного по длине сечения, поэтому его размеры подбирают только для опасного сечения – сечения с максимальным по абсолютному значению изгибающим моментом. К задачам 91...120 К решению задач следует приступать после изучения разделов «Элементы кинематики и динамики» и «Детали машин и механизмы точных приборов», рассмотрения примеров в данных разделах и уяснения приведенных ниже указаний. Движение, при котором, по крайне мере, две точки твердого тела или неизменяемой системы остаются неподвижными, называется вращательным; прямая линия, соединяющая эти две точки, называется осью вращения. Механизмы с вращательным движением звеньев обладают такими достоинствами, как непрерывность и равномерность при малых потерях на трение, а также возможность получения простых и надежных конструкций малых габаритов. Большинство современных машин создается по схеме: Двигатель –> Передача –> Рабочий орган машины Передачами называются механизмы, служащие для передачи механической энергии на расстояние, как правило, с преобразованием вращательных моментов, скоростей, а иногда и характера движения. Основные характеристики передачи, необходимые для выполнения проектировочного расчета: мощность (P1 ,кВт) на ведущем и (P2, кВт) на ведомом валах и угловая скорость ведущего (ω 1, рад/с) и ведомого (ω 2, рад/с) валов либо частота вращения (n1 и n2 ,мин-1). Кроме основных при расчетах часто используются и производные характеристики передач: коэффициент полезного действия, окружная скорость, вращающий момент, передаточное отношение. Коэффициент полезного действия (КПД) η=Р2/Р1; Для многоступенчатых передач общий КПД определяется по формуле: |