Сопротивление материалов. Решение Жесткий брус ав закреплен с помощью шарнирнонеподвижной опоры и поддерживается двумя деформируемыми стальными стержнями ае и вк. На опоре с (рис. 2) две составляющие реакции Z
 Скачать 172.08 Kb. Скачать 172.08 Kb.
|
|
ЗАДАЧА №2 Абсолютно жесткий брус АВ опирается на шарнирно-неподвижную опору и прикреплен с помощью шарниров к двум стальным стержням (рис. 1). Требуется подобрать сечения стержней по условию их прочности, приняв запас прочности по отношению к пределу текучести nт = 2,5. Соотношение площадей поперечных сечений стержней указано на расчетных схема, модуль упругости стали для всех вариантов Е = 2·105 МПа.  Рисунок 1 Дано: а = 1,5 м; b = 1,5 м; с = 1,0 м; Р = 2 кН; Сталь – 40Х; σт = 800 МПа. Решение: Жесткий брус АВ закреплен с помощью шарнирно-неподвижной опоры и поддерживается двумя деформируемыми стальными стержнями АЕ и ВК. На опоре С (рис. 2) – две составляющие реакции ZС и YС, реакции в стержнях направлены вдоль их осей и приложены к брусу АВ в точках А и В.  Рисунок 2 Для плоской системы сил в общем случае ее приложения к конструкции можно составить только три независимых уравнения равновесия. В рассматриваемой задаче к брусу АВ приложено четыре неизвестных усилия: две реакции в шарнире и два усилия в стержнях. Разность между числом неизвестных усилий (N1, N2, ZС, YС) и числом уравнений статики (ΣМС = 0, ΣZ = 0, ΣY = 0) показывает, что для определения этих неизвестных необходимо составить еще одно уравнение, в которое входили бы интересующие нас величины. Такое уравнение или несколько подобных уравнений можно получить из геометрических зависимостей между деформациями элементов заданной конструкции. Таким образом, степень статической неопределимости конструкции равна n = 4 – 3 = 1. Или говорят, что конструкция 1 раз статически неопределима. Рассмотрим конструкцию после деформации ее элементов (рис. 3). Под действием силы Р жесткий брус может повернутся вокруг точки С, при этом стержни АЕ и ВК будут деформированы. Точки А и В описывают при повороте бруса дуги окружностей, которые ввиду малости перемещений заменяют касательными, т.е. считается что эти точки перемещаются по перпендикулярам к радиусам АС и ВС этих дуг. Точка А смещается вверх и занимает положение А1, точка В – вниз, занимая положение В1. Брус, как абсолютно жесткий элемент конструкции, – положение А1В1. Очевидно, что стержень ВК сжат и стал короче на величину ВВ1 = Δl2. Соединив точки Е и А1, находим на чертеже положение стержня АЕ после его деформации. Опустив перпендикуляр из точки А1 на первоначальное положение оси стержня – прямую АЕ, находим точку А2.  Рисунок 3 Отрезок АА2 = Δl1 – удлинение стержня АЕ. Действительно, Δl1 = А2Е – АЕ, и стержень АЕ растянут. Выяснив направление усилий в стержнях, показываем векторы этих уравнений на схеме недеформированного состояния конструкции (рис. 2) и составляем уравнение ее равновесия: 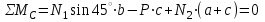 . (1) . (1)Определения составляющих реакции ZС, YС для решения данной задачи не требуется, и два других уравнения статики не составляются. Для вычисления усилий в стержнях N1 и N2 необходимо иметь еще одно уравнение, называемое уравнением совместности деформаций. Это уравнение получаем из геометрических соотношений между деформациями элементов заданной конструкции. При этом ввиду малости деформации изменением угла наклона стержня АЕ пренебрегаем, считая что  Тогда  . .Из подобия треугольников А1АС и В1ВС находим соотношение между деформациями стержней Δl1 и Δl2:  ; ;  ; ;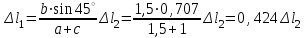 . (2) . (2)Полученная зависимость (2) называется условием совместности деформаций. Определяем длины стержней по заданной схеме конструкции:  ; ;  . .Абсолютные удлинения стержней можно выразить через усилия, используя формулу Гука: 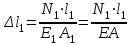 ; ;  (3) (3)Подставив выражения (3) в условие совместности деформаций (2), получим  ; ; . (4) . (4)Решая систему уравнений (1) и (4), определяем усилия в стержнях N1, N2. Для этого подставим значение N1 из (4) в уравнение (1):  ; ; ; ; . .Получаем  ; ; . .Определив усилия в стержнях, переходим к подбору площадей их поперечных сечений. Для заданного материала вычислим допускаемое напряжение 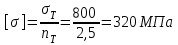 . .Определяем напряжения в стержнях и выбираем большее: 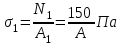 ; ; . .Площадь сечения А подбираем по условию прочности наиболее нагруженного стержня. Так как σ2 больше σ1, используем условие прочности первого стержня:  ; ;  ; ; . .Площади сечений стержней принимаем в соответствии с заданным соотношением:  ; ;  . . |
