Методические указанияКМРИЗ. Методические указания к лабораторным работам первого цикла по компьютерным методам решения инженерных задач Волгоград 2006
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
Методика выполнения
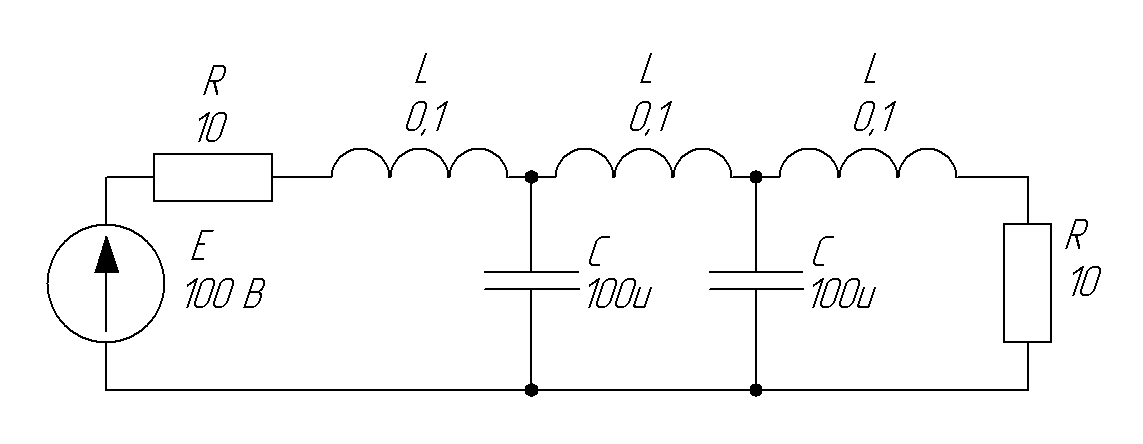 Рисунок 2.2 – принципиальная схема
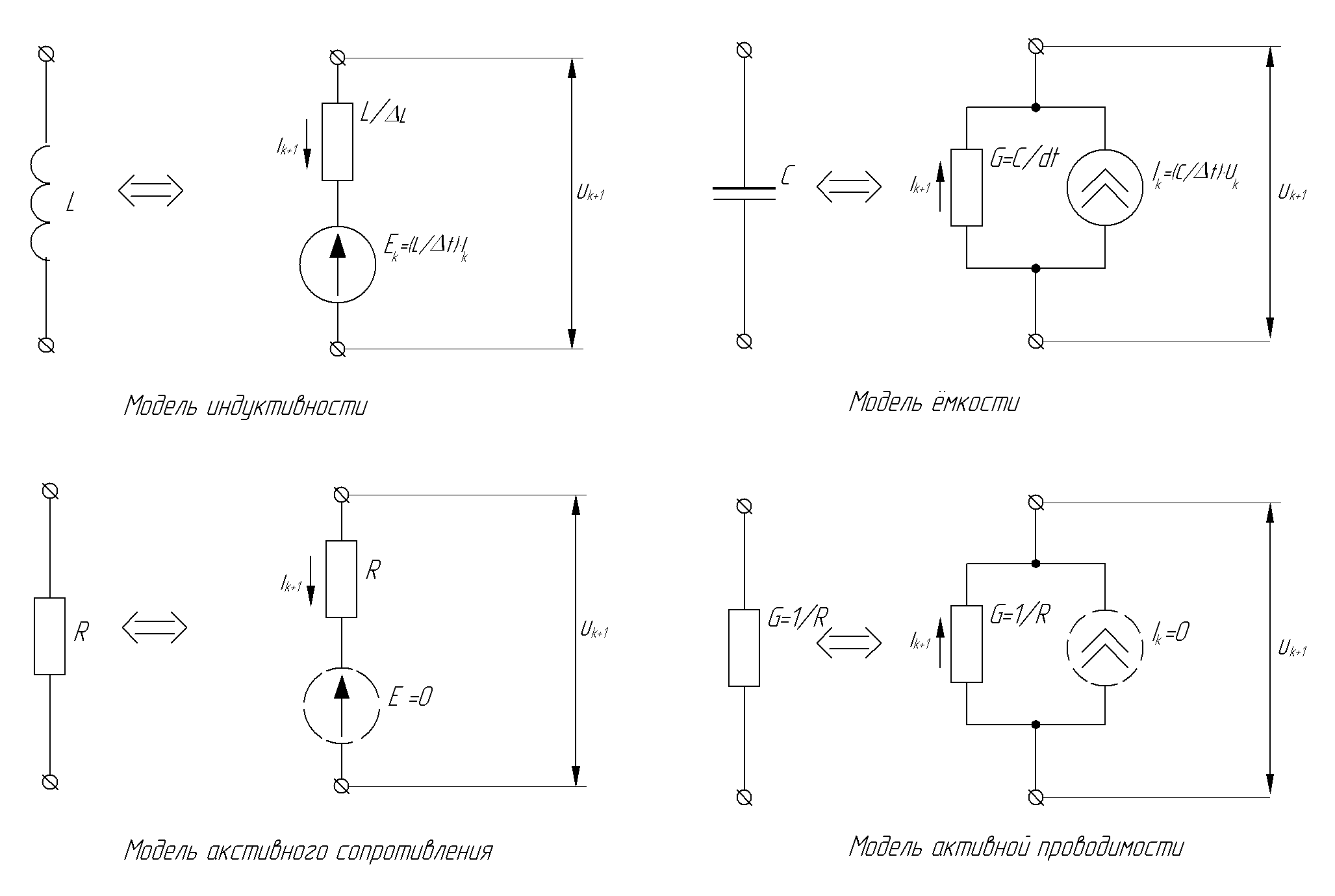 Рисунок 2.3 Конечноразностные модели основных элементов электрических схем Так, для примера рис.2.2 получим модель вида: 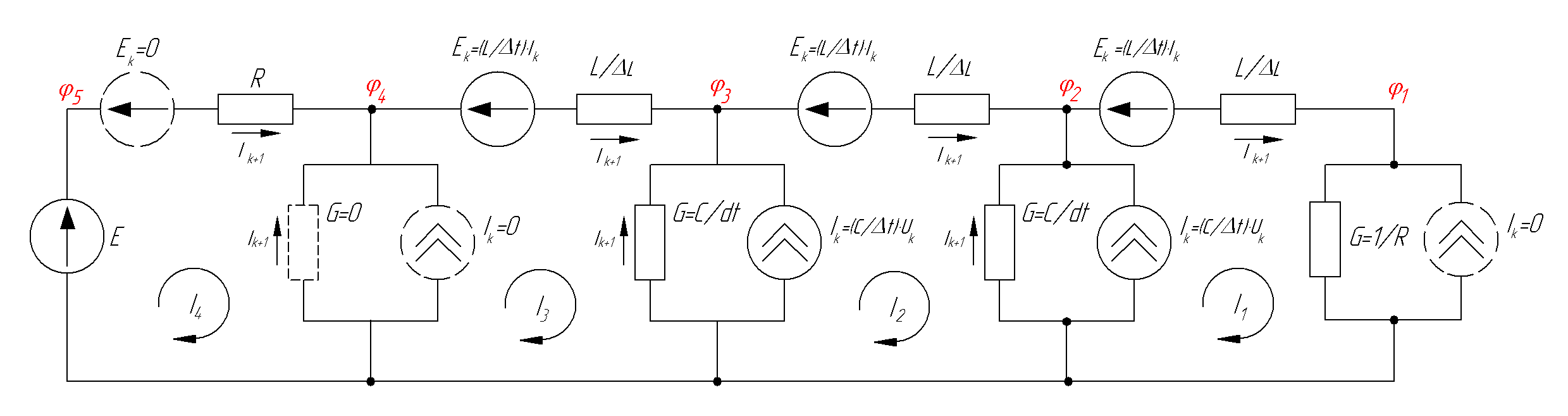 Рисунок 2.4 Конечноразностная модель схемы, изображённой на рис.2.2
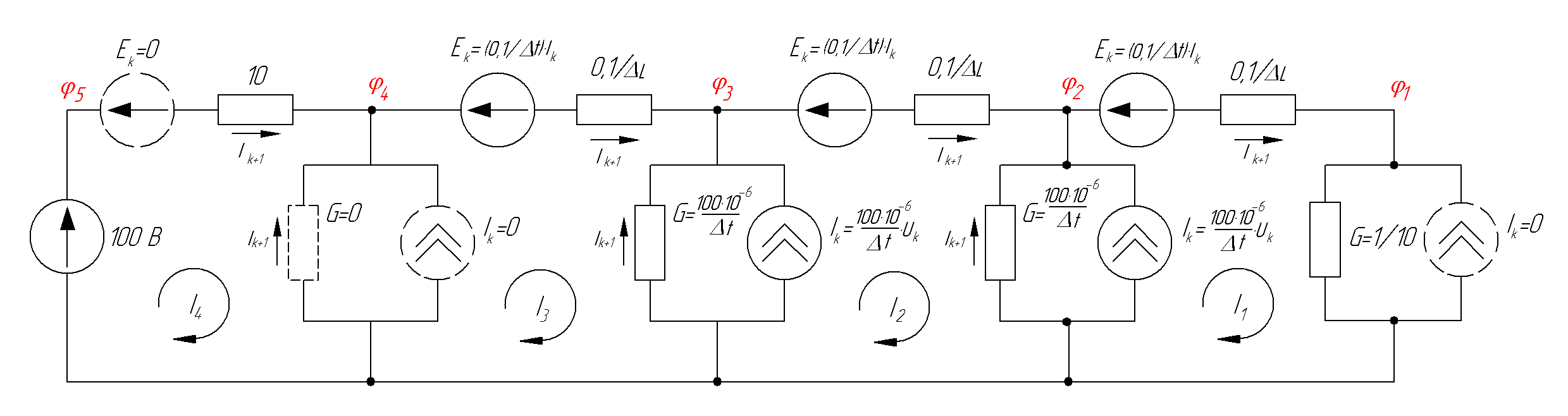 Рисунок 2.5 Конечноразностная модель схемы, изображённой на рис.2.2
Так например, если какому-либо элементу присвоен тип is_R, то этот элемент является чисто активным, если присвоен тип is_LC, то элемент является чисто реактивным.
 Рисунок 2.6 – Панель программирования приложения MathCad

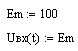 10. Создать алгоритм расчёта мгновенных значений контурных токов на всех элементах схемы: 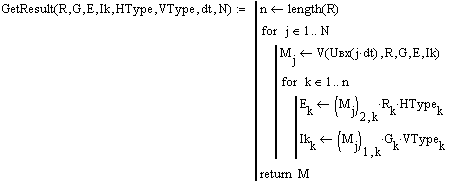
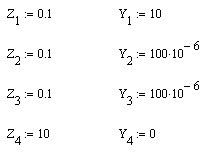 12. Указать значение интервала времени, через которые будут вычисляться мгновенные значения токов и потенциалов (временной интервал дискретизации): 13. Задать двумерный массив элементов, в котором первый столбец содержит значения сопротивлений конечно-разностной схемы замещения, а второй – её проводимости (при этом следует заметить, что заполнение массива происходит сверху вниз при нумерации элементов схемы замещения справа налево). Количество строк в этом массиве равно количеству независимых контуров в конечно-разностной модели рис.2.4 (для рассматриваемого примера – четыре): 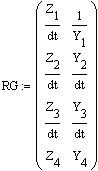 14. Задать массив типов элементов в соответствии с принятыми выше глобальными переменными: 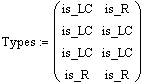 15. Задать массив начальных значений напряжений (первый столбец) и токов проводимостей (второй столбец) на реактивных элементах схемы, например в случае нулевых начальных значений записать: 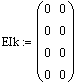 17. Задать число расчётных точек и создать переменную индексации элементов схемы: 18. Выполнить расчёт мгновенных значений контурных токов и потенциалов в узлах схемы путём вызова программы расчёта, описанной выше: Результат вычислений - вектор данных Data, который содержит два подвектора мгновенных значений контурных токов и потенциалов в узлах схемы. При этом мгновенные значения потенциала 19. Определить вектор мгновенных значений искомой величины в соответствии с вариантом задания, например: - напряжение на элементе Z2 равно разнице потенциалов - ток, протекающий через этот элемент численно равен контурному току I2: 20. Построить временную зависимость для искомой величины, например для напряжения на элементе Z2: 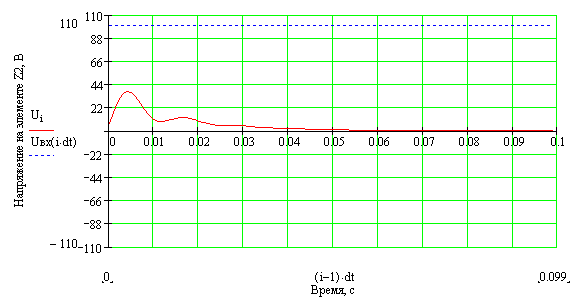 Используя операцию трассировки (слежения) определить не менее 15 координат точек, принадлежащих рассчитанной кривой и занести их в таблицу: Таблица 2.2 – Временная зависимость величины напряжения на элементе Z2
23. Вернуться к шагу 9 и изменить форму входного сигнала. После выполнения автоматического пересчёта, пронаблюдать изменение переходного процесса расчётной величины, например: - синусоидальное воздействие: 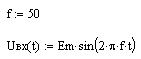 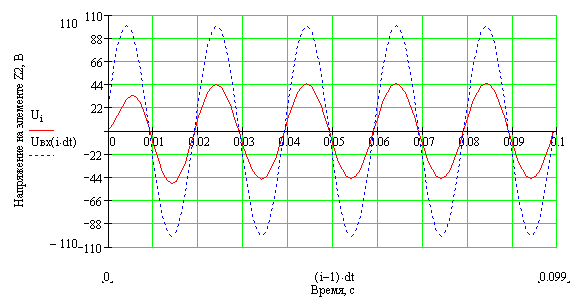 - импульсное напряжение с П-образной формой биполярных импульсов: 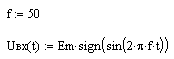 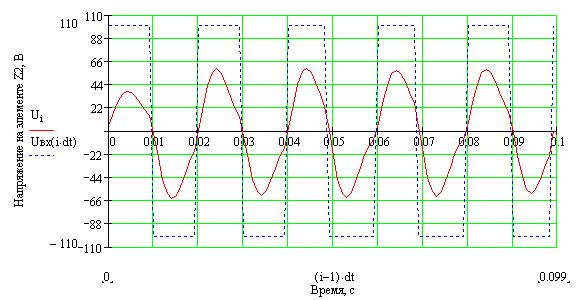 - импульсное напряжение с П-образной формой однополярных импульсов: 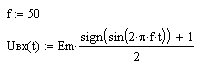 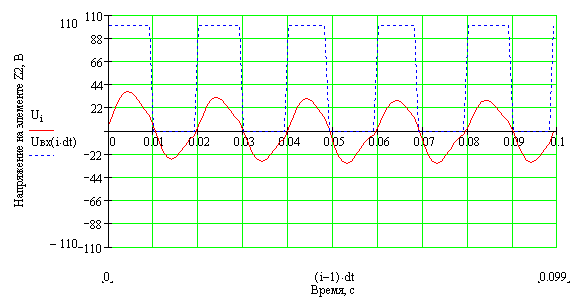 - выпрямленное двухполупериодное напряжение: 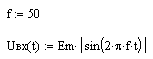 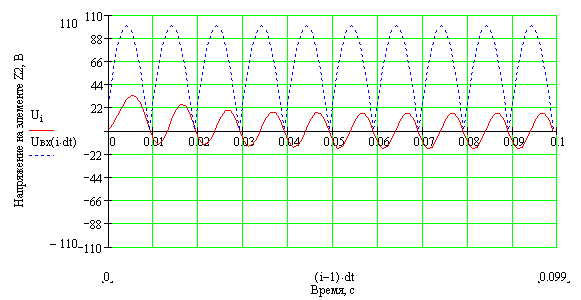 - выпрямленное однополупериодное напряжение: 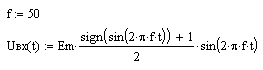 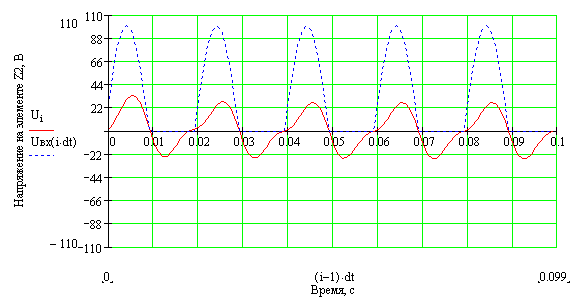 - пилообразные импульсы напряжения: 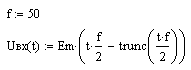 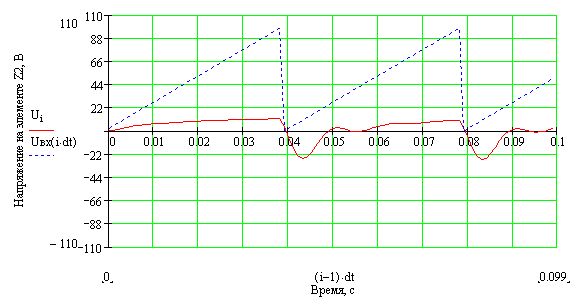 24. Сделать выводы по проделанной работе Контрольные вопросы
Рекомендуемый библиографический список
Лабораторная работа №3 Компьютерные методы расчёта переходных процессов в нелинейных электрических цепях Цель работы: освоить компьютерные методы расчёта переходных процессов в нелинейных электрических цепях и проверить экспериментальным путём влияние шага итерации по времени на устойчивость вычислительного процесса. Краткие теоретические сведения Нелинейные электрические цепи являются наиболее сложными в аналитическом расчёте, так как в этом случае помимо разработки математических моделей нелинейных элементов от инженера требуется умение составлять и решать системы нелинейных дифференциальных уравнений. Сложность расчёта возрастает с увеличением сложности схемы и количества содержащихся в ней элементов. Кроме того, наиболее важным для инженера является выявление особенностей работы исследуемой схемы при подаче на её вход сигналов разной формы при различных условиях окружающей среды, что увеличивает громоздкость и сложность вычислений в несколько раз. Следует также отметить, что во многих случаях получить аналитическое решение, удобное для практического применения вообще не представляется возможным. Одним из методов решения подобных задач является составление конечно-разностных моделей в виде схем замещения, которые описывают работу исследуемого устройства. Процесс построения такой модели тоже является трудоёмкой задачей. Кроме того, он требует от инженера внимательности и хороших знаний в области электротехники. Но в итоге, моделируя различные входные воздействия, подаваемые на схему, инженер экономит очень много времени по сравнению с аналитическим расчётом. В тех случаях, когда составить систему конечно-разностных уравнений затруднительно, но исходная схема может быть приведена лестничному виду, можно применить алгоритм расчёта, исследованный в предыдущей работе. Для этого необходимо в лестничную схему внести нелинейные источники тока и напряжения, нелинейность которых описывается функционально на основе разработанных заранее математических моделей нелинейных элементов. Отчёт должен содержать:
Программа работы
Варианты заданий В качестве математической модели туннельного диода будет использоваться выражение: где Iд – сила тока, протекающего через туннельный диод; U – падение напряжения на туннельном диоде, В; a, b, c, d – коэффициенты математической модели. Вариант задания выдаётся преподавателем каждой бригаде студентов из таблицы 3.1: Таблица 3.1 – Варианты заданий
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
