лаб кос. Указания_к_лабораторным_работам_Косыгина. Методические указания к лабораторным работам Составитель Сухарев В. В. Москва ргу им. А. Н. Косыгина 2018 удк 003. 023
 Скачать 2 Mb. Скачать 2 Mb.
|
Решение системы линейных уравненийПусть есть система линейных уравнений (рис. 20). 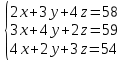 Рисунок 20 Решим эту систему с использованием типовых возможностей Microsoft Excel двумя способами. Первый способ – метод обратной матрицы Запишем систему уравнений в Excel
Рисунок 21 Решение системы линейных уравнений возможно только в том случае, если определитель матрицы не равен нулю. Поэтому первоначально рассчитаем определитель матрицы. Для этого используем функцию МОПРЕД( ). В свободной ячейке записывается функция МОПРЕД( ), в качестве параметра функции передается диапазон ячеек матрицы коэффициентов (рис. 21). В нашем случае определитель матрицы равен -27, поэтому решение системы уравнений возможно. Далее для решения необходимо определить обратную матрицу. Для это используется функция МОБР( ). Чтобы вычислить обратную матрицу, нужно - выделить область ячеек, в которую будет помещен результат. Выделенная область должна совпадать по размерам с исходной матрицей; - в строке формул записать функцию МОБР(диапазон), в качестве аргумента функции передается диапазон ячеек с исходной матрицей; - нажать CTRL+SHIFT+ENTER Чтобы решить систему уравнений, нужно умножить обратную матрицу на столбец свободных членов. Для перемножения используется функция МУМНОЖ( ). Функция имеет два аргумента. В качестве первого передается диапазон ячеек с обратной матрицей, в качестве второго – диапазон ячеек со свободными членами. Порядок осуществления вычислений: - выделить диапазон ячеек для ответов (в нашем случае – три вертикальные ячейки); - в строке формул записать функцию МУМНОЖ(Матрица;Столбец) - нажать CTRL+SHIFT+ENTER Внимание! Если при вычислении обратной матрицы и умножения нажать ENTER – вычисления будут произведены только для одной ячейки! Если все сделано правильно , то в столбец ответов будут подставлены результаты 5,8,6. Соответственно, X = 5, Y = 8, Z = 6. Общий вид задания и решения приведен на рисунке 22 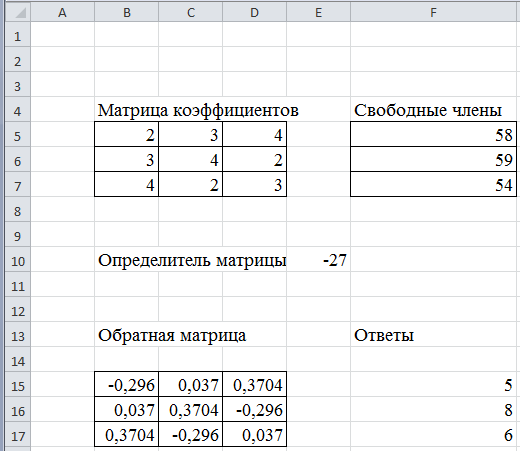 Рисунок 22 Использованные функции с примерами записи для контрольного примера Вычисление определителя: = МОПРЕД(B5:D7) Вычисление обратной матрицы: =МОБР(B5:D7) Умножение матрицы на столбец: =МУМНОЖ(B15:D17;F5:F7) Второй способ решения системы линейных уравнений – использование метода Крамера. Для того, чтобы проверить, не является ли матрица вырожденной и что указанная система уравнений имеет только одно решение, найдем определитель матрицы. Так как исходные данные у нас те же, то определитель матрицы у нас уже рассчитан. Далее, согласно методу Крамера, столбцы матрицы поочередно меняются на столбец свободных членов и для каждой полученной матрицы рассчитывается определитель. Вычисления приведены на рисунках 23-25.
Рисунки 23- 25 Решения уравнений рассчитываются как отношения определителей полученных матриц к определителю исходной матрицы В нашем случае получается X = - 135 / (-27) = 5 Y = - 216 / (-27) = 8 Z = - 162 / (-27) = 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
