Измерение модуля Юнга. Измерение модуля Юнга проволоки. Методические указания к лабораторной работе по курсу физики для студентов всех специальностей
 Скачать 200.5 Kb.
|
0,2 %), называется пределом текучести σт (точка С на кривой). В области СD деформация возрастает без заметного увеличения напряжения, то есть тело как бы течёт. Эта область называется областью текучести. Материалы, для которых область текучести значительна, называются вязкими, для которых же она практически отсутствует – хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности σпр. В рамках данной работы исследование деформаций твёрдых тел ограничено изучением только малых продольных растяжений, при которых выполняется закон Гука. Согласно этому закону деформации пропорциональны силам, их вызывающим.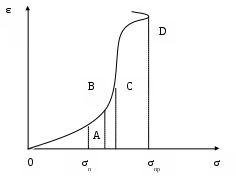 σ  σу  рис.1. Предположим, что к торцам однородного стержня приложены растягивающие или сжимающие силы F (Рис.2). Стержень окажется деформированным, то есть сжатым или растянутым. Мысленно проведём произвольное сечение С, перпендикулярное к оси стержня. Для равновесия стержня АС необходимо, чтобы на его нижнее основание С действовала сила  . Это сила, с которой нижняя часть стержня действует на верхнюю. Эта сила возникает вследствие деформации стержня. Верхняя часть стержня также деформирована и действует на нижнюю с силой равной  и противоположно направленной. Аналогичным образом можно описать силы в любом поперечном сечении растянутого или сжатого стержня. Силу, отнесённую к единице площади поперечного сечения стержня, называют напряжением σ: σ =  . Упрощенная запись закона Гука, известная из курса физики средней школы, F=kΔl с использованием коэффициента жёсткости k, не совсем удобна, поскольку этот коэффициент зависит не только от свойств материала, но и от размеров и формы упругого тела. Последнее обстоятельство исключает поиск коэффициента жёсткости в справочной литературе и затрудняет его использование. К тому же следует отметить нарушение причинно-следственной связи, поскольку причиной удлинения стержня Δl является внешняя сила F, приложенная к стержню. F F A F A C B B F F1 F B C F1  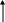  Error: Reference source not foundа в рис.2 Поэтому более удобной записью закона Гука является такая запись, в которой при малых упругих деформациях относительное удлинение ε =  оказывается пропорциональным напряжению σ. Коэффициентом пропорциональности является величина обратная постоянной Е, называемой модулем Юнга (1773- 1829)ε =  =  Модуль Юнга определяется физическими свойствами материала детали и его легко можно найти в справочной литературе. Обычно модуль Юнга определяют как напряжение σ, которое надо приложить к стержню, чтобы его длина удвоилась. Безусловно надо думать, что эта ситуация не всегда реальна, так как при таких больших деформациях закон Гука почти для всех тел становится недействительным: тело либо разрушается, либо нарушается пропорциональность между деформацией и приложенным напряжением. Следует отметить, что закон Гука является приближённым. Закон Гука и основанные на нём расчёты верны с относительной ошибкой порядка относительного удлинения. Более общим, чем закон Гука, является утверждение, что в случае упругих деформаций напряжение является однозначной функцией относительного удлинения σ = σ (ε). При этом однако следует помнить, что причиной удлинения и напряжения, возникающего в стержне, является внешняя сила. Эта функция должна обращаться в нуль при ε = 0, так как с исчезновением деформации исчезает и напряжение σ. Поэтому в разложении функции σ (ε) в ряд по степеням ε должен отсутствовать нулевой член, и разложение должно иметь вид σ =Е* ε + А* ε²+ B*ε³…, причём коэффициенты Е, А, В … являются постоянными, зависящими только от материала стержня и его физического состояния. Если относительное удлинение ε мало, то высшими степенями ε можно пренебречь. Такими образом закон Гука и основанные на нём расчёты верны с относительной ошибкой порядка ε. Отметим, что относительное удлинение можно определить выражением ( Δl)/l поскольку  Свойства материалов при деформациях, вообще говоря, изменяются. Однако при малых деформациях изменениями упругих постоянных можно пренебречь. Отсюда вытекает принцип суперпозиции малых деформаций: если на тело действует несколько сил, то для вычисления результирующей деформации можно вычислить сначала деформации, вызываемые каждой силой в отдельности, а затем полученные деформации сложить. Опыт показывает, что под действием растягивающей или сжимающей силы F изменяются не только продольные, но и поперечные размеры стержня. Пусть а0 - толщина стержня до деформации, а – после деформации. За толщину стержня можно принять для круглого стержня его диаметр, для прямоугольного - одну из сторон его прямоугольного основания. Если сила F растягивающая, то величина -  называется относительным поперечным сжатием стержня ( ). Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона (1781—1840):  Коэффициент Пуассона зависит только от материала тела и является одной из важных постоянных, характеризующих его упругие свойства. Модуль Юнга Е и коэффициент Пуассона μ полностью характеризуют упругие свойства изотропного материала. Все прочие упругие постоянные могут быть выражены через Е и μ. Лабораторная установка и методика экспериментаСхема установки для определения модуля Юнга изображена на рис.3. Она включает в себя кронштейн А, на котором закреплена исследуемая стальная проволока Б длиной  , указанной на стенде. К концу проволоки прикреплён штифт В с площадкой для грузов Г. На штифт нанесена кольцевая риска для наблюдения за растяжением проволоки. Абсолютное растяжение проволоки  измеряется с помощью катетометра В-630, описание которого вынесено в приложение.Error: Reference source not found 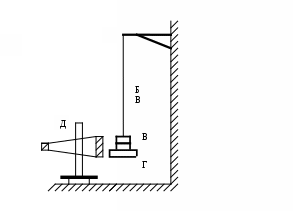 Б А В Г Д Рис.3. рис. 3 Приборы и принадлежности: исследуемая стальная проволока на кронштейне, набор грузов, микрометр и катетометр В-630. Порядок проведения измерений 1.Наблюдая в зрительную трубу верхний край кольцевой риски, нанесённой на штифт, совмещают его при помощи винта 4 с горизонтальным штрихом в поле зрения трубы. Делают начальный отсчёт  по отсчётному микроскопу.2.Нагружают проволоку первым грузом. Кольцевая риска для отсчёта при этом смещается вверх. Винтом 4 перемещают каретку со зрительной трубой до совпадения горизонтального штриха в поле зрения трубы с тем же краем кольцевой риски на штифте, что и при начальном отсчёте. Делают отсчёт с первой нагрузкой  . Заносят результат в таблицу. Абсолютное удлинение проволоки  равно  .3. Прибавляют ещё один груз и аналогичным образом определяют новое удлинение при увеличенной нагрузке. Начальный отсчёт остаётся прежним.4. Проводят те же измерения с 3 и 4 грузами, суммируя их массу. Результаты заносят в таблицу. 5. С помощью микрометра измеряют диаметр проволоки  и подсчитывают площадь поперечного сечения проволоки.6.Списывают со стенда общую длину проволоки  в миллиметрах.7. Все результаты измерений и расчётов заносят в таблицу:
Обработка результатов экспериментаПодставляют измеренные величины в формулу  и для каждого измерения подсчитывают модуль Юнга. По данным таблицы строят график зависимости  и делают вывод относительно правомерности использования принципа суперпозиции малых деформации при проведении измерений. Оценивают погрешность результатов в соответствии с методическими указаниями по обработке результатов измерений.Содержание и оформление отчёта по работе. В отчёте по работе должны содержаться: название работы, цель работы, основные теоретические сведения, таблица измерений, расчёты модуля Юнга, график зависимости и подсчёт погрешности модуля Юнга, выводы по работе.Вопросы для самопроверки1.Что такое деформация? Какую деформацию называют упругой, пластической? Назовите виды деформаций. 2.Как возникают силы упругости? Как они направлены? 3.В чём состоит закон Гука? При каких условиях он справедлив? 4.В чём состоит принцип суперпозиции малых деформаций? 5.Что такое модуль Юнга? Физический смысл модуля Юнга. 6.Что характеризует коэффициент Пуассона? ЛитератураСивухин Д.В. Общий курс физики. Том 1, Механика. М.: Наука, 1974. Трофимова Т.И. Курс физики. Москва, Высшая школа, 1998. 3. Савельев И.В. Курс общей физики. Том 1. М.: Наука, 1990. 4. Методические указания к оформлению лабораторных работ по физике. Сост. Л.А.Евсеева. Саратов: СПИ, 1980. Приложение. Катетометр В-630 Катетометр В-630 предназначен для бесконтактного измерения вертикальных координат. Катетометр (см. Рис.4) состоит из основания 17, колонки 3 и измерительной каретки 8. Катетометр выставлен вертикально по круглому уровню 2 так, чтобы при вращении колонки на любой угол пузырёк не сходит с центра более, чем на 0,5 деления. . 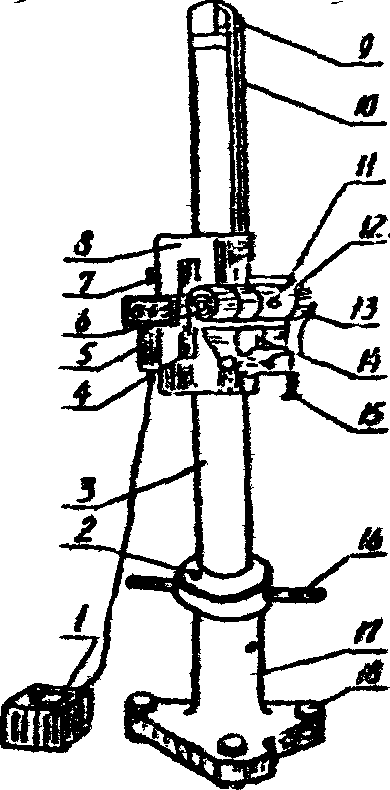 Колонка 3 установлена внугри основания 18, и ее можно поворачивать вокруг вертикальной оси с помо- щью рукояток 16. На каретке 8 смонтированы визир- ная труба 13, блок уровня 14 и отсчётный микроскоп ее корпуса. В колонку вмонтирована 630-миллиметр- овая шкала в оправе, видимая в отраженном свете. Грубое перемещение каретки 8 по вертикали произ- водится вручную при откреплённом винте 7, точное с помощью микроскопического винта 4 при закреп- лённом винте 7. Каретка уравновешена противовесом, расположенным внутри колонки. Противовес соединен с кареткой стальным тросом 10, переброшенным через направляющий ролик 9. Визирная труба 13 имеет фоку- сирующую линзу, перемещением которой с помощью маховичка 11 осуществляется наводка на резкость изображения выбранных точек измеряемого объекта. рис.4Пределы измерения с помощью катетометра по вертикали составляют 0-630 мм. Интервалы расстояний от защитного стекла объектива с различными насадочными линзами до объекта 280-480 мм, 420-810 мм, 700-1810 мм, без насадочных линз 1810-∞ мм. Предел допускаемой основной погрешности прибора не более (10+L/1ОО)мкм; где L, мм - расстояние от защитного стекла объектива до объекта измерения . Установка визирной трубы в вертикали по уровню производится микрометрическим винтом 15. Наводка на резкость изображений масштабной сетки, штрихов шкалы пузырька уровня, наблюдаемых в одном поле зрения, осуществляется окуляром 6. Масштабная сетка в вертикальном и горизонтальном направлении разделена на 10 частей. Отсчетный микроскоп установлен так, что 10 горизонтальных штрихов сетки укладываются между двумя штрихами миллиметровой шкалы. Следовательно, в вертикаль ном направлении каждому штриху соответствует одна десятая миллиметра. В горизонтальном направлении десятая часть всей шкалы равна одной сотой миллиметра. Работа с прибором производится в следующем порядке: - подключите трансформатор 1 в розетку сеть питания; - открепите винт 7 и переместите измерительную каретку 8 на уровень выбранной точки объекта; - установите окуляр визирной трубы 6 на резкость изображений масштабной сетки, шкалы и пузырька уровня; - произведите наводку на резкость изображения измеряемого объекта, пользуясь маховичком 11. Затем с помощью микрометрического винта 4, при закрепленном винте 7, произведите точную наводку визирной трубы на выбранную точку объекта; - наблюдая в окуляр, совместите изображения концов пузырька уровня винтом 15 (рис.5,а). \ Сетка визирной трубы имеет перекрестие, левый горизонтальный штрих которого выполнен в виде углового биссектора (рис.5,6).      а б      рис.5 При наводке визирной трубы выбранная точка объекта должна располагаться точно посередине углового биссектора на уровне горизонтального штриха. При точной наводке следите за тем, чтобы концы пузырька уровня образовывали дугу. В поле зрения окуляра одновременно видны изображения двух штрихов миллиметровой шкалы, обозначенной крупными цифрами, и масштабная сетка. Один из штрихов пересекает масштабную сетку и выходит на светлое наклонное поле. Крупная цифра у штриха обозначает целые миллиметры. Десятые доли отсчитывают по вертикальной шкале масштабной сетки, сотые доли - по горизонтальной шкале масштабной сетки в том месте, где штрих выходит на середину светлого наклонного поля. Тысячные доли миллиметра оцениваются на глаз. |
,м
,Па