Методические указания к выполнению контрольных работ по курсу Электротехника
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Часть II Краткие теоретические сведения Электрической цепью называется физический объект работающий на принципе использования энергии электромагнитного поля. Она состоит из источника электрической энергии, приёмника (нагрузки) и замкнутого проводящего контура. В электрической цепи (схеме) различают узлы, ветви и контуры. Узел – точка цепи (схемы), где сходятся не менее 3 ветвей. Ветвь – участок цепи (схемы), соединяющий два узла, во всех элементах которого протекает один и тот же ток. Контур – замкнутый путь, проходящий по нескольким ветвям цепи (схемы). Различают источники напряжения (ЭДС) и источники тока. Идеальным источником напряжения (ЭДС) называется источник напряжение, которого не зависит от нагрузки. Это возможно, если внутреннее сопротивление источника равно нулю (rвн=0). Идеальным источником тока называется источник, ток которого не зависит от нагрузки. Это возможно, если внутреннее сопротивление источника равно бесконечности(rвн=∞). Расчёт линейных электрических цепей базируется на законах Ома и двух законах Кирхгофа. Напомним, что закон Ома для участка цепи связывает ток, напряжение и сопротивление на данном участке. Первый закон Кирхгофа (закон узла) гласит – алгебраическая сумма токов в узле равна нулю. Алгебраическая сумма подразумевает учёт знака – например, подтекающий ток берётся со знаком (+), а вытекающий со знаком (-) или наоборот. Второй закон Кирхгофа (закон контура) гласит – алгебраическая сумма ЭДС действующая в замкнутом контуре равна алгебраической сумме падений напряжений в этом же контуре. В цепи синусоидального тока законы Кирхгофа форматируются как геометрическая (векторная) сумма. Условно электрические цепи можно разделить на простые и сложные. Простой электрической цепью будем называть цепь, содержащую один источник и любое число сопротивлений. В свою очередь расчет простых цепей можно свести к двум задачам: прямая- это когда задана ЭДС (напряжения) источника и все сопротивления. Такая задача решается в два этапа, т.е. цепь надо свернуть и определить эквивалентное сопротивление, а потом развернуть т.е. определить токи. Примером является решение задачи 1.4 пособия. Рекомендуется эту задачу разобрать подробно. В обратной задаче заданы все сопротивления и ток (напряжение или мощность) в одном элементе цепи. Надо определить остальные токи и напряжения ЭДС источника. Такая задача решается с использованием законов Ома и Кирхгофа. Сложной электрической цепью называется цепь, содержащая два или более источников электрической энергии в различных ветвях. Для расчета такой цепи её надо описать системой независимых уравнений, решив которую определим все токи ветвей и напряжения и мощности всех участков. Далее рассмотрены алгоритмы расчета простых и сложных электрических цепей постоянного и синусоидального тока, а также алгоритм расчета трёхфазных цепей. 2.1 Алгоритм расчета простых электрических цепей постоянного тока (задачи 1.1 -1.4) Простая электрическая цепь рациональнее решается методом преобразования (свёртки). В заданной электрической цепи необходимо заменить последовательно и параллельно соединенные сопротивления R, определить эквивалентное сопротивление: а) используя найденное эквивалентное сопротивление и развернув цепь, определить токи во всех ветвях; б) составить систему уравнений по методу законов Кирхгофа*; в) составить и решить систему уравнений по методу контурных токов и далее по заданию. Проверить расчет электрической цепи, используя баланс мощностей, т.е. 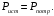 Мощность, вырабатываемая источником: 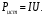 Мощность, потребляемая потребителями: 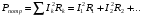 Для определения входного сопротивления, необходимо замкнуть клеммы источника ЭДС и по известной методике свернуть полученную цепь относительно зажимов выбранной ветви. Алгоритм расчёта электрической цепи методом законов Кирхгофа 1) Определяем число ветвей (токов) в цепи и число узлов, введя их условные обозначения. 2) По известным направлениям источников ЭДС или тока выбираем условные положительные направления токов в ветвях, указывая их стрелочками. Напомним, что направления падений напряжений на резисторах UK совпадают с направлением токов IК в пассивном элементе ветви. 3) Составляем n-1 независимых уравнений по первому закону Кирхгофа, где n – число узлов схемы. При этом токи, входящие в узел, берутся со знаком плюс (+), в противном случае-- со знаком минус (–). 4) Недостающее число уравнений (y–n+1) составляется по второму закону Кирхгофа (y-число ветвей). При этом рекомендуется выбирать наиболее «простые» контуры, т.е. содержащие наименьшее число ветвей и элементов цепи. Направление обхода контура указывается стрелкой. В уравнениях ЭДС входят со знаком (+), если их направление совпадает с направлением обхода контура, в противном случае – со знаком (–). Аналогично, падения напряжений UK=IKRK берутся со знаком (+), если они совпадают по направлению с обходом контура в противном случае со знаком минус (–). Если цепь содержит источник тока, то этот ток известен и его определять не надо. 5) Составленная система уравнений решается относительно искомых токов. 6) Проверку расчёта цепи удобнее выполнить по балансу мощностей или по второму закону Кирхгофа. Недостатком этого метода является высокая степень полученной системы уравнений, что иногда затрудняет расчёт. Метод контурных токов устраняет этот недостаток. Алгоритм расчёта электрических цепей методом контурных токов 1) Для упрощения расчёта рекомендуется источники тока, если они имеются в схеме, преобразовать в эквивалентные источники ЭДС или выбрать соответствующие независимые контуры с источником тока, а направление их обхода указать стрелками. 2) Вычислить собственные RКК и взаимные RКn сопротивления контуров и величины контурных ЭДС ЕКК . 3) Для выбранных контуров составить систему уравнений по второму закону Кирхгофа с учётом выше изложенных рекомендаций, учитывая, что по взаимным сопротивлениям Rkn протекает два контурных тока, которые создают падения напряжений, совпадающие по направлению с соответствующим током, и их необходимо учитывать с соответствующим знаком. 4) Решить полученную систему уравнений любым известным методом. 5) Действительные значения токов ветвей определяются как алгебраическая сумма контурных токов, протекающих по данной ветви. Алгоритмы расчёта электрических цепей методом узловых напряжений (потенциалов) Перед началом расчёта рекомендуется источники ЭДС преобразовать в источники тока. 1) Обозначить узлы электрической цепи. 2) Принять потенциал одного из узлов равным нулю (заземлить). 3) Для оставшихся узлов записать систему уравнений, соответствующую данному методу. 4) Вычислить собственные qКК и взаимные qКn проводимости узлов. 5) Вычислить узловые токи IКK. 6) Решить систему уравнений (п.3) относительно потенциалов узлов. 7) Используя закон Ома и Кирхгофа, определить токи в ветвях. 8) Проверить расчёт цепи на основании баланса мощностей или по законам Кирхгофа. Алгоритм расчета цепей однофазного синусоидального тока (задачи 2.1 – 2.3) 1) По известным параметрам цепи (L и C) и угловой частоте 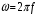 определяем модули реактивных сопротивлений определяем модули реактивных сопротивлений 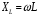 и и 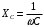 (индуктивность подставлять в Генри, а емкость – в Фарадах). (индуктивность подставлять в Генри, а емкость – в Фарадах). 2) Записать комплексы полных сопротивлений всех ветвей 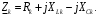 3) Записать комплексы действующих значений, заданных ЭДС (напряжений) цепи. Здесь возможны два варианта: а) напряжение источника задано модулем, например, U= 220 В. Полагаем U=U=220 В, т.е. совмещаем напряжение U с вещественной осью (+1) комплексной плоскости и с этим допущением рассчитываем цепь; б) напряжение (ЭДС) источника задано в функции времени. Например, 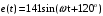 . Комплексная амплитуда ЭДС . Комплексная амплитуда ЭДС 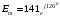 , комплекс действующего значения , комплекс действующего значения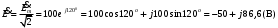 . .4) Дальнейший алгоритм расчета цепей синусоидального тока полностью совпадает с алгоритмом расчета цепей постоянного тока, только все действия выполняются над комплексными числами. В результате расчета получим значение тока в комплексной форме. 5) Выражение для мгновенного значения тока i(t) или напряжения u(t) получают в порядке, обратном пункту 3, т.е. по алгебраической форме комплекса тока (напряжения) записывается показательная форма действующего значения, по ней комплексная амплитуда Im. и по комплексной амплитуде – функция времени i(t). 6) Показание ваттметра определяется по выражению 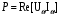 , где , где 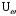 - комплекс действующего значения напряжения, на которое включен ваттметр, - комплекс действующего значения напряжения, на которое включен ваттметр, 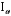 - сопряженный комплекс тока, протекающего по ваттметру. - сопряженный комплекс тока, протекающего по ваттметру. Сопряженным комплексом называется комплексное число, отличающееся от заданного знаком перед мнимой частью. 7) По найденным значениям токов и напряжений строится векторная диаграмма, которая представляет собой векторное исполнение законов Кирхгофа. Алгоритм расчета трехфазных цепей (задача 3.1, 3.2) Алгоритм расчета трехфазных цепей зависит от схемы соединения генератора, потребителя и от характера нагрузки. В рассматриваемом случае, при схеме соединения «звезда» - «звезда» необходимо учесть не симметрию нагрузки и состояние нулевого (нейтрального) провода. а) При симметричной нагрузке расчет ведется по одной фазе (фазе А), а величины двух других фаз находятся путем умножения на 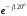 и и 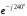 . .б) В случае несимметричной нагрузки и включенном нулевом проводе расчет трехфазной цепи ведется по всем фазам самостоятельно. Для этого изображаем трехфазную электрическую цепь и символическим методом определяем все токи и напряжения в фазах. Так как сопротивление нулевого провода равно нулю (Z0 = 0; g0= ∞), то напряжение смещения нейтрали равно нулю. Следовательно, напряжение на фазах эквивалентного приемника равны ЭДС соответствующих фаз 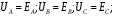 Определяем линейные (фазные) токи: 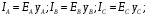 2) Определяем ток нулевого провода: 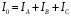 . . 3) По найденным значениям комплексов токов и напряжений (ЭДС) строим векторную диаграмму. 4) Определяем мощности фаз. Мощности трехфазной системы, независимо от характера нагрузки и положения нулевого провода, определяется как сумма соответствующих мощностей определенных фаз 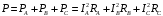 . . По этим данным строится векторная диаграмма. в) Нулевой провод отключен и нагрузка неравномерная. В этом случае порядок расчета следующий. 1) Определим проводимость фаз 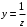 (См). (См).2) Определим ЭДС фазы генератора 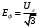 (В). (В). 3) Определим напряжение между нулевыми точками, т.е. напряжение смещения нейтрали, например 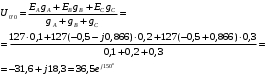 4) Определяем напряжение на фазах потребителя, используя второй закон Кирхгофа: 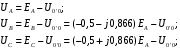 5) Определяем линейные (фазные) токи: 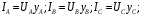 6) Определим мощности фаз и всей схемы: 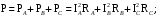 Q= 0 т.к. P=S. Q= 0 т.к. P=S.7) По найденным значениям комплексных токов и напряжений строим векторную диаграмму. Методические указания для расчета цепей несинусоидального тока (задача 4.1) Несинусоидальные токи и напряжения в электрических цепях возникают вследствие наличия различных нелинейных элементов, в том числе полупроводниковых и ферромагнитных. Несинусоидальная функция, удовлетворяющая условию Дирихле, может быть разложена в ряд Фурье, который можно записать, например, в виде: 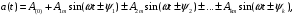 где 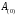 - постоянная составляющая, которая характеризуется нулевой частотой - постоянная составляющая, которая характеризуется нулевой частотой  ; ;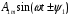 - первая (основная) гармоника, период которой совпадает с периодом несинусоидальной функции. Частота первой гармоники в энергосистеме - первая (основная) гармоника, период которой совпадает с периодом несинусоидальной функции. Частота первой гармоники в энергосистеме 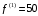 Гц; Гц;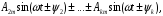 - высшие гармоники (вторая, третья и т.д.). Частота k-ой гармоники в k раз выше частоты 1- ой гармоники - высшие гармоники (вторая, третья и т.д.). Частота k-ой гармоники в k раз выше частоты 1- ой гармоники 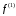 Линейные электрические цепи при воздействии несинусоидального напряжения (тока) рассчитываются методом наложения. Таким образом, расчет заданной цепи надо вести для каждой гармоники и постоянной составляющей отдельно. Линейные электрические цепи при воздействии несинусоидального напряжения (тока) рассчитываются методом наложения. Таким образом, расчет заданной цепи надо вести для каждой гармоники и постоянной составляющей отдельно.Расчет по постоянной (нулевой) составляющей. Ее частота 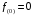 , следовательно , следовательно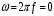 , тогда реактивные сопротивления , тогда реактивные сопротивления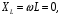 , а , а 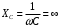 . . Таким образом, по постоянной составляющей индуктивность представляет собой закороченный участок, а емкость – обрыв данной ветви. В итоге получаем резистивную схему замещения цепи. Величины токов в ветвях определяются только сопротивлениями резистивных элементов R. Напряжения на конденсаторе определяются его схемой включения и рассчитывается из уравнения, записанного по второму закону Кирхгофа. Расчет по первой(основной) гармонике ведется символическим методом. Сопротивление реактивных элементов в задаче обычно задаются по первой гармонике. Исходя из этого, записываем комплексы сопротивлений всех ветвей 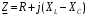 . .Дальнейший алгоритм расчета зависит от поставленной задачи и подробно рассматривается далее. Расчет по высшим гармоникам ведется, так же символическим методом, как и по первой, но только необходимо помнить, что реактивные сопротивления XL и XC зависят от частоты, 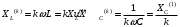 , ,т.е. сопротивление индуктивности растет пропорционально номеру гармоники – k, а сопротивление емкости падает обратно пропорционально номеру гармоники. Закон Ома для участка цепи для k-ой гармоники имеет вид: 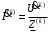 . .Более подробно рассмотрено в расчете цепей однофазного синусоидального тока. Следует помнить, что токи и напряжения различных гармоник имеют разные частоты, поэтому нельзя складывать их комплексы, а также строить векторные диаграммы разных гармоник в одной плоскости. |
