Методические указания к выполнению контрольной работы для студентов заочной формы обучения

• Название: Методические указания к выполнению контрольной работы для студентов заочной формы обучения
• Дата: 06.04.2023
• Размер: 210.26 Kb.
• Имя файла: ekonometrika_6369004.docx
• Тип: Методические указания; #1041588
• страница: 2 из 8

Для оценки качества полученного уравнения регрессии рассчитывают теоретический коэффициент детерминации – R²_yx: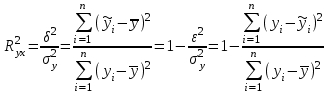

,

где ² – объясненная уравнением регрессии дисперсия y;

²- остаточная (необъясненная уравнением регрессии) дисперсия y;

²_y - общая (полная) дисперсия y.

Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака y, объясняемую регрессией (а, следовательно, и фактором х), в общей вариации (дисперсии) y. Коэффициент детерминации R²_yx принимает значения от 0 до 1. Соответственно величина 1-R²_yx характеризует долю дисперсии y, вызванную влиянием прочих неучтенных в модели факторов и ошибками спецификации.

При парной линейной регрессии R²_yx=r²_yx.

Оценка статистической значимости параметров уравнения регрессии.

С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y). Если оценку параметров произвести по данным другого статистического наблюдения (другому набору значений x и y), то получим другие численные значения , .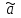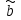

Мы предполагаем, что все эти наборы значений x и y извлечены из одной и той же генеральной совокупности. Чтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез.

В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности. В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение определяется в зависимости от уровня значимости () и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений.

Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля.

Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля, например, при уровне значимости =0,05.

Для параметра b критерий проверки имеет вид: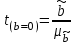

,

где 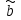- оценка коэффициента регрессии, полученная по наблюдаемым данным;

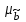– стандартная ошибка коэффициента регрессии.

Для линейного парного уравнения регрессии стандартная ошибка коэффициента вычисляется по формуле: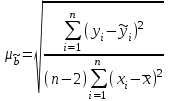

.
Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: .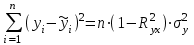

Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид: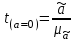

,

где 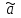- оценка параметра регрессии, полученная по наблюдаемым данным;

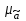– стандартная ошибка параметра a.

Для линейного парного уравнения регрессии: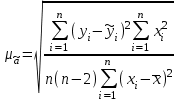

.

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий: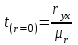

, где r_yx - оценка коэффициента корреляции, полученная по наблюдаемым данным; _r – стандартная ошибка коэффициента корреляции r_yx.

Для линейного парного уравнения регрессии: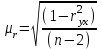

.

В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t_(b=0)=t_(r=0).
Прогноз ожидаемого значения результативного признака y по линейному парному уравнению регрессии.

Пусть требуется оценить значение признака-результата для заданного значения признака-фактора (х^р). Прогнозируемое значение признака-результата c доверительной вероятностью равной (1-) принадлежит интервалу прогноза: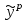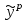

( -t·_p; +t·_p),

где 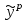- точечный прогноз;

t – коэффициент доверия, определяемый по таблицам распределения Стьюдента в зависимости от уровня значимости  и числа степеней свободы (n-2);

_p- средняя ошибка прогноза.

Точечный прогноз рассчитывается по линейному уравнению регрессии, как: .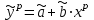

Средняя ошибка прогноза определяется по формуле: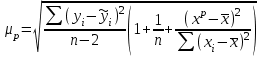

.

Задание № 1

На основе данных, приведенных в Приложении 1 и соответствующих Вашему варианту (таблица 2), требуется:

1. 
   Рассчитать коэффициент линейной парной корреляции и построить уравнение линейной парной регрессии одного признака от другого. Один из признаков, соответствующих Вашему варианту, будет играть роль факторного (х), другой – результативного (y). Причинно-следственные связи между признаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.
   
2. 
   Определить теоретический коэффициент детерминации и остаточную (необъясненную уравнением регрессии) дисперсию. Сделать вывод.
   
3. 
   Оценить статистическую значимость уравнения регрессии в целом на пятипроцентном уровне с помощью F-критерия Фишера. Сделать вывод.
   
4. 
   Выполнить прогноз ожидаемого значения признака-результатаy при прогнозном значении признака-фактора х, составляющим 105% от среднего уровня х. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
   

Таблица 2

Вариант	Номер начального наблюдения	Номер конечного наблюдения	Номер признаков из прил. 1	Вариант	Номер начального наблюдения	Номер конечного наблюдения	Номер признаков из прил. 1
1	2	3	4	5	6	7	8
01		50	1,2	51	26	75	1,3
02	1	50	3,4	52	26	75	4,5
03	2	51	1,3	53	27	76	1,4
04	2	51	4,5	54	27	76	2,5
05	3	52	1,4	55	28	77	1,5
06	3	52	2,5	56	28	77	2,3
07	4	53	1,5	57	29	78	1,2
08	4	53	2,3	58	29	78	3,4
09	5	54	1,2	59	30	79	1,3
10	5	54	3,4	60	30	79	4,5
11	6	55	1,3	61	31	80	1,4

Продолжение табл. 2

1	2	3	4	5	6	7	8
12	6	55	4,5	62	31	80	2,5
13	7	56	1,4	63	32	81	1,5
14	7	56	2,5	64	32	81	2,3
15	8	57	1,5	65	33	82	1,2
16	8	57	2,3	66	33	82	3,4
17	9	58	1,2	67	34	83	1,3
18	9	58	3,4	68	34	83	4,5
19	10	59	1,3	69	35	84	1,4
20	10	59	4,5	70	35	84	2,5
21	11	60	1,4	71	36	85	1,5
22	11	60	2,5	72	36	85	2,3
23	12	61	1,5	73	37	86	1,2
24	12	61	2,3	74	37	86	3,4
25	13	62	1,2	75	38	87	1,3
26	13	62	3,4	76	38	87	4,5
27	14	63	1,3	77	39	88	1,4
28	14	63	4,5	78	39	88	2,5
29	15	64	1,4	79	40	89	1,5
30	15	64	2,5	80	40	89	2,3
31	16	65	1,5	81	41	90	1,2
32	16	65	2,3	82	41	90	3,4
33	17	66	1,2	83	42	91	1,3
34	17	66	3,4	84	42	91	4,5
35	18	67	1,3	85	43	92	1,4
36	18	67	4,5	86	43	92	2,5
37	19	68	1,4	87	44	93	1,5
38	19	68	2,5	88	44	93	2,3
39	20	69	1,5	89	45	94	1,2
40	20	69	2,3	90	45	94	3,4
41	21	70	1,2	91	46	95	1,3
42	21	70	3,4	92	46	95	4,5
43	22	71	1,3	93	47	96	1,4
44	22	71	4,5	94	47	96	2,5
45	23	72	1,4	95	48	97	1,5
46	23	72	2,5	96	48	97	2,3
47	24	73	1,5	97	49	98	1,2
48	24	73	2,3	98	49	98	3,4

Окончание табл. 2

1	2	3	4	5	6	7	8
49	25	74	1,2	99	50	99	1,3
50	25	74	3,4	0	50	99	4,5

МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, который в свою очередь включает 2 круга вопросов: отбор факторов и выбор уравнения регрессии.

Отбор факторов обычно осуществляется в два этапа:

1) теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;

2) количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции):

r_y,yr_y,x1r_yx2 .... r_y,xm

r_x1,yr_x1,x2r_x2x2 .... r_x2,xm

......

r_xm,yr_xm,x1r_xm,x2 .... r_xm,xm

где r_y,xj– линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками yи хj j=1;m, m -число факторов.

r_xj,xk– линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками хjи хk j,k=1;m.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).

2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).

3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность - тесная линейная связь между факторами.

Мультиколлинеарность может привести к нежелательным последствиям:

1) оценки параметров становятся ненадежными. Они обнаруживают большие стандартные ошибки. С изменением объема наблюдений оценки меняются (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

2) затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

3) становится невозможным определить изолированное влияние факторов на результативный показатель.