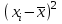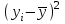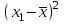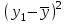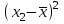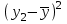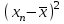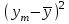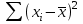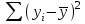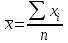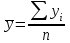Методические указания к выполнению контрольной работы для студентов заочной формы обучения
 Скачать 210.26 Kb.
|
ЭКОНОМЕТРИКАМетодические указания к выполнению контрольной работы для студентов заочной формы обучения Содержание Общие указания 4 Введение 6 Линейный парный регрессионный анализ 8 Задание №1 15 Множественный регрессионный анализ 17 Задание №2 24 Системы эконометрических уравнений 25 Задание №3 32 Временные ряды в эконометрических исследованиях 35 Задание № 4 42 Список литературы 44 Приложение 1 45 Приложение 2 48 ОБЩИЕ УКАЗАНИЯ Контрольная работа по дисциплине эконометрика выполняется для приобретения студентами опыта построения эконометрических моделей, принятия решений спецификации и идентификации моделей, выбора методов оценки параметров модели, интерпретации результатов, получения прогнозных оценок. При выполнении контрольной работы следует обратить внимание на следующие требования: Задания к контрольной работе составлены в 100 вариантах. Каждый студент выполняет один вариант. Номер его варианта соответствует последним двум цифрам номера его зачетной книжки. Замена задач не допускается. Номер варианта указывается в самом начале работы. Работы можно выполнять с помощью вычислительной техники и специального программного обеспечения (например, электронных таблиц MS Excel). 3. Нельзя ограничиваться приведением только готовых ответов. Расчеты должны быть представлены в развернутом виде, применяя где это необходимо табличные оформления исходной информации и расчетов, со всеми формулами, пояснениями и выводами, соблюдая достаточную точность вычислений. В пояснениях и выводах показать, что именно и как характеризует исчисленный показатель. 4. Работа должна быть написана разборчиво, без помарок. Титульный лист оформляется в соответствии с примером, приведенном в Приложении 2. Работа должна содержать список использованной литературы, быть подписана студентом, указана дата выполнения работы. 5. Контрольная работа должна быть представлена не позже, чем за 2 недели до экзамена (зачета). 6. Если работа не принимается к зачету, то она вместе с рецензией возвращается студенту. Студент обязан учесть все замечания и внести их в текст работы или выполнить ее заново; при этом рецензия преподавателя должна быть приложена к работе. Несамостоятельно выполненные работы рассматриваются как неудовлетворительные. ВВЕДЕНИЕ Эконометрика – наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов. Эконометрика связывает между собой экономическую теорию и экономическую статистику и с помощью математико-статистических методов придает конкретное количественное выражение общим закономерностям, устанавливаемым экономической теорией. Предметом эконометрики являются массовые экономические явления. Главным инструментом эконометрики служит эконометрическая модель, которая представляет собой либо одно уравнение; либо систему уравнений. Эконометрика изучает массовые явления в экономике через статистические совокупности, а последние через признаки, которыми характеризуются единицы этой совокупности. Признаки могут находиться в связи между собой. Взаимосвязанные признаки могут выступать в одной из ролей: - роли признака-результата (аналог зависимой переменной (y) в математике); - роли признака-фактора, значения которого определяют значение признака-результата (аналог независимой переменной (x) в математике). Связи классифицируют по степени тесноты, направлению, форме, числу факторов. По степени тесноты связи делят на статистические (стохастические) и функциональные. Статистическая (стохастическая) связь – это такая связь между признаками, при которой для каждого значения признака-фактора х признак-результат (y) может в определенных пределах принимать любые значения с некоторыми вероятностями; при этом его статистические (массовые) характеристики (например, среднее значение) изменяются по определенному закону. Статистическая связь обусловлена: 1) тем, что на результативный признак оказывают влияние не только фактор (факторы), учтенные в модели, но и неучтенные или неконтролируемые факторы; 2) неизбежностью ошибок измерения значений признаков. Модель статистической связи может быть представлена в общем виде уравнениями: yi=f(x1i,ui) (i=1,2,…,n) - для модели с одним фактором, yi=f(x1i,...,xmi,ui), (i=1,2,…,n) – для модели с множеством факторов, где yi - фактическое значение результативного признака для i-ой единицы статистической совокупности; f(x1i,...,xmi) - часть результативного признака, сформировавшаяся под воздействием учтенных известных факторных признаков (xji, j=1;m); ui - часть результативного признака, сформировавшаяся под воздействием неконтролируемых или неучтенных факторов, а также ошибок измерения признаков. Противоположной статистической связи является функциональная. Функциональной называется такая связь, когда каждому возможному значению признака-фактора (х) соответствует одно или несколько строго определенных значений результативного признака (y). Определение функциональной связи может быть легко обобщено для случая многих признаков х1, х2,…,хm. модель функциональной связи в общем виде можно представить уравнением: yi=f(x1i,...,xmi). По направлению изменений результативного и факторного признаков связи делят на прямые и обратные. По форме связи (виду функции f) связи делят на прямолинейные (линейные) и криволинейные (нелинейные). По количеству факторов в модели связи подразделяют на однофакторные (парные) и многофакторные. ЛИНЕЙНЫЙ ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ Одним из методов изучения стохастических связей между признаками является регрессионный анализ. Регрессионный анализ представляет собой вывод уравнения регрессии, с помощью которого находится средняя величина случайной переменной (признака-результата), если величина другой (или других) переменных (признаков-факторов) известна. Он включает следующие этапы: 1) выбор формы связи (вида аналитического уравнения регрессии); 2) оценку параметров уравнения; 3) оценку качества аналитического уравнения регрессии. Наиболее часто для описания статистической связи признаков используется линейная форма. Внимание к линейной связи объясняется четкой экономической интерпретацией ее параметров, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. В случае линейной парной связи уравнение регрессии примет вид: 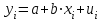 . Параметры данного уравнения а и b оцениваются по данным статистического наблюдения x и y. 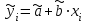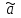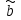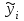Результатом такой оценки является уравнение:  , где  ,  - оценки параметров a и b,  - значение результативного признака (переменной), полученное по уравнению регрессии (расчетное значение).Наиболее часто для оценки параметров используют метод наименьших квадратов (МНК). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (u) и независимой переменной (x). Задача оценивания параметров линейного парного уравнения методом наименьших квадратов состоит в следующем: получить такие оценки параметров 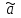, , 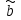при которых сумма квадратов отклонений фактических значений результативного признака - yiот расчетных значений – 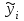минимальна. Формально критерий МНК можно записать так: 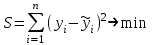 .Проиллюстрируем суть данного метода графически. Для этого построим точечный график по данным наблюдений (xi,yi, i=1;n) в прямоугольной системе координат (такой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.   y       y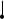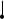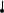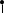’i yi  xх i Математическая запись данной задачи: 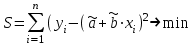 .Значения yi и xii=1;n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров - 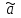, 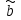. Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е. 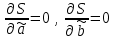 . В результате получим систему из 2-ух нормальных линейных уравнений: 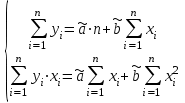 Решая данную систему, найдем искомые оценки параметров: 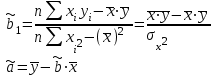 Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм 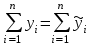 (возможно некоторое расхождение из-за округления расчетов).Для расчета оценок параметров 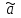, 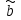можно построить таблицу 1.Знак коэффициента регрессии b указывает направление связи (если b>0, связь прямая, если b<0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения. Формально значение параметра а – среднее значение y при х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра а не имеет смысла. Оценка тесноты связи между признаками осуществляется с помощью коэффициента линейной парной корреляции - rx,y. Он может быть рассчитан по формуле: 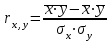 . Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: 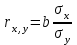 .Область допустимых значений линейного коэффициента парной корреляции от –1 до +1. Знак коэффициента корреляции указывает направление связи. Если rx,y>0, то связь прямая; если rx,y<0, то связь обратная. Если данный коэффициент по модулю близок к единице, то связь между признаками может быть интерпретирована как довольно тесная линейная. Если его модуль равен единице rx,y =1, то связь между признаками функциональная линейная. Если признаки х и y линейно независимы, то rx,y близок к 0. Для расчета rx,y можно использовать также таблицу 1. Таблица 1
|
