Методические указания к выполнению контрольной работы для студентов заочной формы обучения
 Скачать 210.26 Kb. Скачать 210.26 Kb.
|
|
3) Устранение влияния сезонной составляющей из исходного ряда динамики : xS= x-Si. Результаты расчета xS для нашего примера представлены в столбце 6 таблицы 9. 4) Аналитическое выравнивание уровней xS (построение тренда): 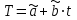 . .Расчет параметров при аналитическом выравнивании чаще всего производится с помощью метода наименьших квадратов (МНК). При этом поиск параметров для линейного уравнения тренда можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю. Для этого вводится новая условная переменная времени ty, такая, что ty =0. Уравнение тренда при этом будет следующим: 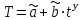 . . При нечетном числе уровней ряда динамики для получения ty=0 уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (периоду или моменту времени, соответствующему данному уровню присваивается нулевое значение). Даты времени, расположенные левее этого уровня, обозначаются натуральными числами со знаком минус (-1 –2 –3 ...), а даты времени, расположенные правее этого уровня – натуральными числами со знаком плюс (1 2 3 ...). Если число уровней ряда четное, периоды времени левой половины ряда (до середины) нумеруются –1, -3, -5 и т.д. А периоды правой половины - +1, +3, +5 и.т.д. При этом ty будет равна 0. Система нормальных уравнений (соответствующих МНК) преобразуется к виду: 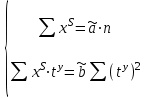 Отсюда параметры уравнения рассчитываются по формулам: 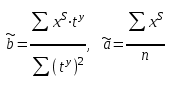 . .Интерпретация параметров линейного уравнения тренда 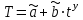 : : 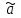 - уровень ряда за период времени tу=0; - уровень ряда за период времени tу=0; 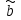 - средний абсолютный прирост уровня ряда за единичный промежуток времени. - средний абсолютный прирост уровня ряда за единичный промежуток времени.В нашем примере четное число уровней ряда: n=12. Следовательно, условная переменная времени для 6-ого элемента ряда будет равна –1, а для 7-ого +1. Значения переменной iy содержатся во 2-ом столбце таблицы 9. Параметры линейного тренда будут: 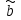 =14257,5/572=24,93; =14257,5/572=24,93; 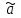 =8845/12=737,08. Это значит, что с каждым кварталом объем выпуска товара в среднем увеличивается на 2∙28,7 усл.ед. А средний за период с 1993 по 1995гг объем выпуска составил 738,75 усл.ед. =8845/12=737,08. Это значит, что с каждым кварталом объем выпуска товара в среднем увеличивается на 2∙28,7 усл.ед. А средний за период с 1993 по 1995гг объем выпуска составил 738,75 усл.ед.Рассчитаем значения трендовой компоненты по формуле 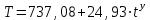 (столбец 7 таблицы 9). (столбец 7 таблицы 9).5) Учет сезонной составляющей в выровненных уровнях ряда ( 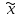 =T+S). Результаты расчета для нашего примера представлены в столбце 8 таблицы 9. =T+S). Результаты расчета для нашего примера представлены в столбце 8 таблицы 9.6) Расчет абсолютной ошибки временного ряда (Е=x- 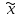 ) осуществляется для оценки качества полученной модели. Результаты расчета для нашего примера представлены в столбце 9 таблицы 9. ) осуществляется для оценки качества полученной модели. Результаты расчета для нашего примера представлены в столбце 9 таблицы 9.Таблица 9
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||