лабы. Лабораторные+работы+в+Multisim. Методические указания к выполнению лабораторных работ по электротехнике и основам электроники. 2011 Рассмотрены и рекомендован к изданию
 Скачать 1.71 Mb.
|
|
Соединение фаз приемника по схеме «звезда». Цель работы: исследовать режимы работы трехфазного приемника, фазы которого соединены по схеме «звезда»: симметричный, несимметричный, несимметричный с нейтральным проводом, обрыв фазы, короткое замыкание фазы. Проверить соотношения между линейными и фазными напряжениями при симметричном и несимметричных режимах, определение роли нейтрального провода. Основные теоретические положения Трехфазной называется электрическая цепь, в различных ветвях которой действуют три одинаковые по амплитуде синусоидальные ЭДС, имеющие одну и ту же частоту, сдвинутые по фазе одна относительно другой на угол 120°  , , ,где ЕАm= ЕBm=ЕCm=Еm - значения ЭДС фаз генератора А, В и С (рис. 5.1). 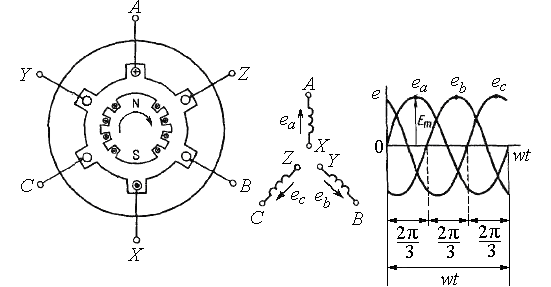 Рис. 5.1. В настоящее время трехфазные системы получили широкое распространение благодаря тому, что: - при одинаковых условиях питание трехфазным напряжением позволяет получить значительную экономию материала проводов по сравнению с тремя однофазными линиями; - трехфазный генератор (при прочих равных условиях) дешевле, легче, надежнее и экономичнее, чем три однофазных генератора такой же общей мощности; - трехфазная система позволяет проще получить вращающееся магнитное поле; - меньше пульсации момента на валу приводного двигателя при равномерной загрузке генератора. Источником системы трехфазных напряжений является трехфазный синхронный генератор, на статоре которого размещаются три фазные обмотки (фазы), смещенные в пространстве относительно друг друга на угол 120°. ЭДС в неподвижных витках обмотки статора индуцируются в результате пересечения этих витков магнитным полем, возбуждаемым током обмотки вращающегося с равномерной скоростью ротора. Расположенная на роторе обмотка возбуждения питается от источника постоянного напряжения. Под действием трехфазной системы ЭДС на зажимах трехфазного потребителя создается трехфазная симметричная система напряжений, сдвинутых по фазе на угол 120°, и имеющих одинаковые амплитудные и действующие значения 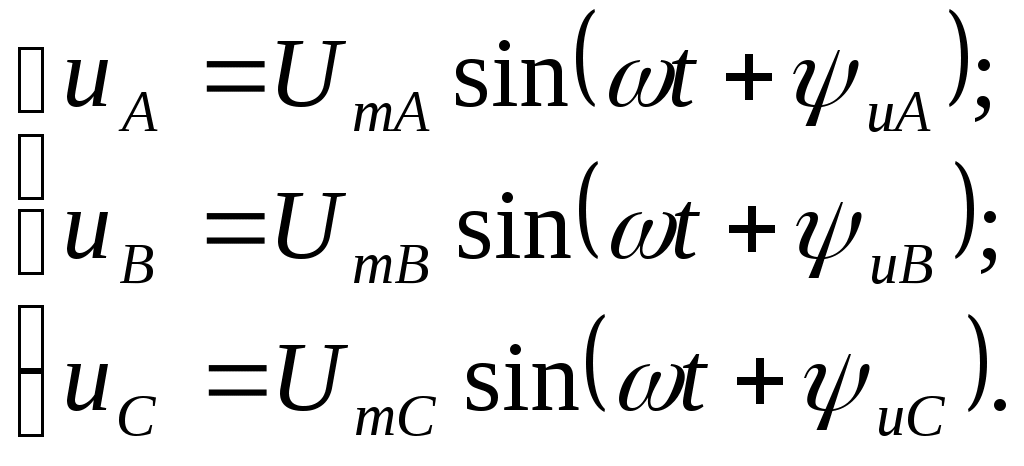 Фазы трехфазного потребителя, так же как и у трехфазного источника, соединяются звездой (рис. 5.2) или треугольником (рис. 5.3). 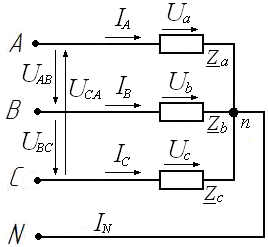 Рис. 5.2. 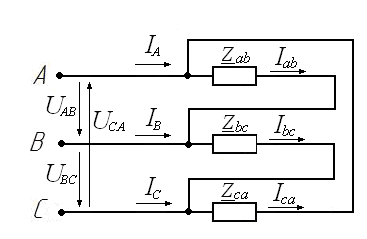 Рис. 5.3. Соединение, при котором концы всех трех фаз потребителя объединяют в общую точку п, называемую нейтральной точкой, а начала фаз подсоединяют к трехфазному источнику питания посредством линейных проводов, называется соединением звездойтрехфазного потребителя. Соединение, при котором конец первой фазы соединяется с началом второй, конец второй с началом третьей, а конец третьей - с началом первой, называется соединением трехфазного потребителя треугольником. Передача электрической энергии от источника к потребителю осуществляется с помощью линейных проводов, причем трехфазная система может быть трехпроводной или четырехпроводной. Четвертый провод - нейтральный (Nn), соединяющий общие точки фаз источника N и потребителя n. В трехфазных электрических цепях различают фазные и линейные напряжения и токи. Токи IA, IB, IC в соответствующих линейных проводах, называются линейными. Токи, протекающие по отдельным фазам – фазными. Ток IN в нейтральном проводе - нейтральным. Фазными называют напряжения между началами и концами отдельных фаз источника или приемника. При соединении звездой, фазными являются напряжения между началами фаз и нейтральной точкой источника или приемника, например, Ua = Ub = Uc . Линейными называются напряжения между линейными проводами, соединяющими начала источника и приемника UAB , UBC , UCA. При соединении потребителя звездой по его фазам протекают те же токи IA, IB, IC, что и по линейным проводам, т.е., при соединении потребителя звездой фазные токи оказываются равными соответствующим линейным токам: IФ = IЛ. Тогда по первому закону Кирхгофа для нейтральной точки n  .По второму закону Кирхгофа при соединении потребителя звездой (независимо от наличия нейтрального провода) между линейными и фазными напряжениями потребителя существуют следующие соотношения  ; ; .Поскольку сопротивления линейных и нейтрального проводов пренебрежимо малы, то линейные напряжения генератора будут равны линейным напряжениям потребителя и соответственно фазные напряжения генератора равны фазным напряжениям потребителя. Векторная диаграмма напряжений потребителя будет совпадать с векторной диаграммой напряжений генератора, причем линейные напряжения потребителя, так же как и фазные, будут сдвинуты относительно друг друга на угол 2π/3 (рис. 5.1). Нагрузка, при которой комплексные сопротивления всех фаз потребителя равны между собой (  ), называется симметричной. При этом  ,  , а напряжение между нейтральными точками UnN=0.Если нагрузка симметрична при соединении фаз потребителя звездой между фазными и линейными напряжениями существует соотношение  .По закону Ома фазные токи потребителя  ,  ;  ,причем фазные токи равны между собой IA=IB=IC=IФ (ввиду равенства фазных напряжений и фазных сопротивлений потребителя) и сдвинуты относительно фазных напряжений на равные углы φa=φb=φc=φф, определяемые из выражений  .При симметричной нагрузке ток в нейтральном проводе, определяемый как векторная сумма фазных токов, оказывается равным нулю, поэтому нейтральный провод можно не применять. Векторная диаграмма для симметричной нагрузке изображена на рис. 5. 4. 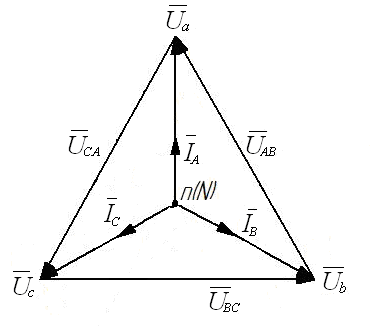 Рис. 5.4. При несимметричной нагрузке комплексные сопротивления всех трех фаз не равны между собой, т.е.  .При наличии нейтрального провода и несимметричной нагрузке геометрическая сумма фазных токов трехфазной системы в соответствии с первым законом Кирхгофа для нейтральной точки равна току в нейтральном проводе  .Если нейтральный провод отключен, то при несимметричной нагрузке потенциал нейтральной точки п потребителя не равен потенциалу нейтральной точки N генератора, т.к. эти точки не соединены между собой. При этом на векторной диаграмме (рис. 5.5) нейтральная точка п потребителя сместится в положение ( 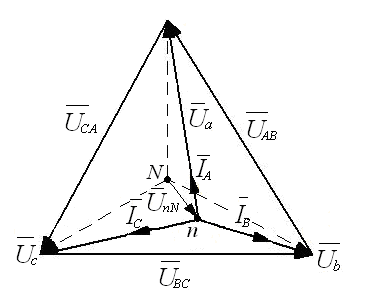 ) в котором геометрическая сумма фазных токов потребителя будет равна нулю  . При этом на одних фазах может быть пониженное напряжение по сравнению с фазными напряжениями генератора, а на других - повышенное. Рис. 5.5. Порядок выполнения работы. 1 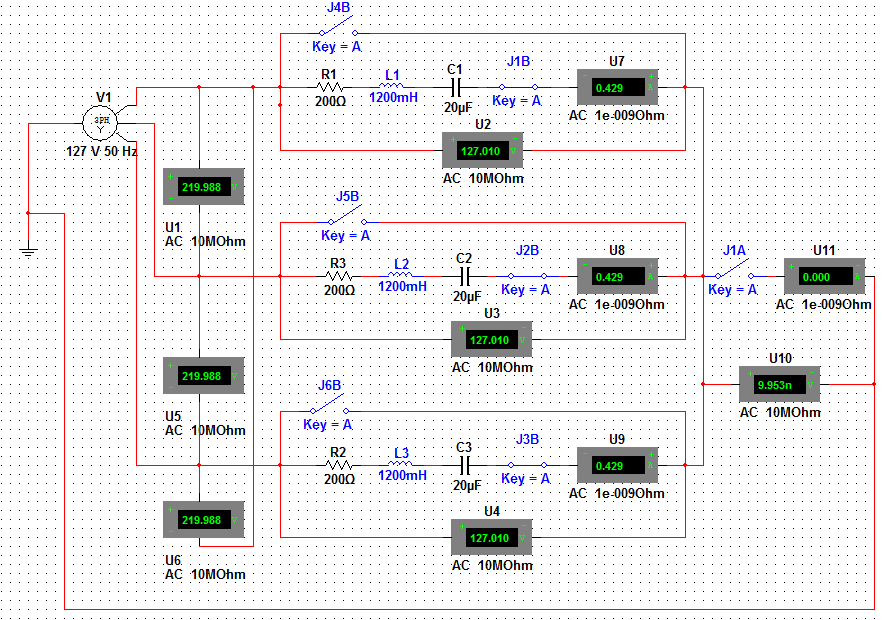 . Собрать на рабочем поле экрана электрическую цепь синусоидального тока с соединением фаз приемника по схеме «звезда» (рис.5.6). Рис. 5.6. Задать параметры элементов цепи согласно варианту (табл. 5.1): Табл. 5.1.
3. Провести опыт при симметричном режиме приемника. Снять показания приборов. Результаты измерений записать в табл. 5.2. 4. Оборвать одну из фаз, разомкнув ключ в этой фазе. Снять показания приборов. Результаты измерений записать в табл. 5.2. 5. Замкнуть одну из фаз накоротко, замкнув соответствующий ключ. Снять показания приборов. Результаты измерений записать в табл. 5.2. 6. Уменьшить параметры элементов в первой фазе в четыре раза, во второй фазе – в два раза. Снять показания приборов. Результаты измерений записать в табл. 5.2. 7. Подключить в схему нейтральный провод, замкнув ключ на нейтральном. Снять показания приборов. Результаты измерений записать в табл. 5.2. Табл. 5.2.
8. По результатам измерений построить векторные диаграммы для каждого опыта. Величины линейных напряжений Uab, Ubc, Ucaне зависят от режима работы трехфазного приемника. Построение векторных диаграмм целесообразно начинать с построения треугольника линейных напряжений. Вектора линейных напряжений строятся согласно масштабу. Вектора фазных напряжений строятся согласно масштабу следующим образом: из вершины треугольника линейных напряжений «А» проводят окружность радиусом, равным фазному напряжению Ua; из вершины треугольника линейных напряжений «В» проводят окружность радиусом, равным фазному напряжению Ub; Из вершины треугольника линейных напряжений «С» проводят окружность радиусом, равным фазному напряжению Uс. Точка пересечения окружностей n будет представлять собой геометрическое место начала векторов фазных напряжений Ua, Ub, Uc(рис. ). Вектора фазных токов Ia, Ib, Ic, стоятся относительно соответствующих фазных напряжений. Ua, Ub, Uc. Углы сдвига фаз φa, φb, φc между фазными напряжениями и токами определяются по формулам:  ;  ; ,где  ;  . При построении векторов токов необходимо учитывать знак угла сдвига фаз. Векторная диаграмма для симметричной нагрузки для случая, рассмотренного на рис. 5.6 (табл. 5.3): Rа = Rb = Rc = 200 Ом, Lа = Lb = Lc = 1200 мГн, Cа = Cb = Cc = 20 мкФ. Табл. 5.3
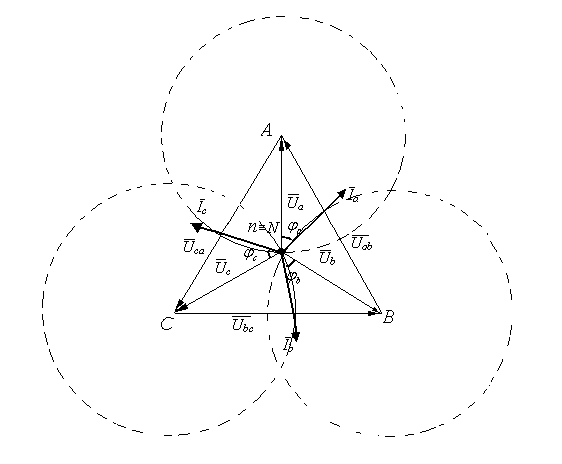 Рис. 5.7. Векторная диаграмма для симметричной нагрузки. Для несимметричной нагрузки (табл. 5.4): Rа = 50 Ом, Lа = 300 Гн, Cа = 5 мкФ; (XL = 31 Ом, XC = 640 Ом); Rb = 100, Lb = 600 Гн, Cb = 10 мкФ; (XL = 188 Ом, XC = 318 Ом); Rc = 200 Ом, Lc = 1200 Гн, Cc = 20 мкФ; (XL = 377 Ом, XC = 159 Ом). Табл. 5.4.
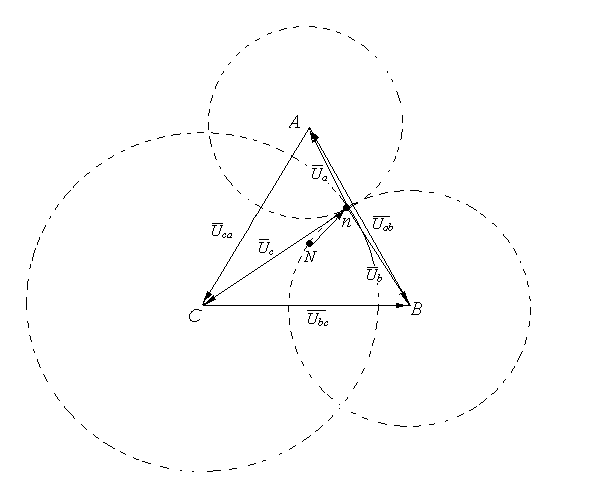 Рис. 5.8. Векторная диаграмма напряжений для несимметричной нагрузки. Контрольные вопросы: 1. Что такое симметричная трехфазная система напряжений? Какое устройство является источником системы трехфазных напряжений? 2. Каким образом осуществляется схема соединения фаз потребителя по схеме «звезда»? 3. Дать определение фазных и линейных напряжений. Дать определение фазных и линейных токов. 4. Какая нагрузка называется симметричной? 5. Каково соотношение между линейными и фазными напряжениями при соединении фаз симметричного приемника по схеме «звезда»? Каково соотношение между линейными и фазными токами при соединении фаз симметричного приемника по схеме звезда? В каких случаях применяется четырехпроводная система электроснабжения? Каково значение нейтрального провода? Как вычислить ток в нейтральном проводе? Лабораторная работа № 6. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||