лабы. Лабораторные+работы+в+Multisim. Методические указания к выполнению лабораторных работ по электротехнике и основам электроники. 2011 Рассмотрены и рекомендован к изданию
 Скачать 1.71 Mb.
|
|
7. Рассчитать значение емкости конденсатора, при которой в цепи возникнет резонанс:  .Задать значение емкости конденсатора, равную резонансному значению С0. Снять показания приборов и заполнить таблицу. Построить векторную диаграмму цепи. Контрольные вопросы. Записать выражения законов Ома и Кирхгофа для цепей переменного тока. 2. Каким образом осуществляется последовательное соединение элементов в электрической цепи? 3. Записать формулы для определения индуктивного и емкостного сопротивлений. 4. Записать формулы для определения активной, реактивной и полной мощности цепи. 5. Что такое резонанс напряжений? Условия возникновения резонанса напряжений? Изменением каких параметров электрической цепи можно обеспечить в ней режим резонанса напряжений? Лабораторная работа № 4. Параллельное соединение резистора, катушки и конденсатора в цепи переменного тока. Цель работы: опытным путем проверить основные законы для цепи переменного тока с параллельным соединением приемников электрической энергии: резистора, катушки индуктивности и конденсатора. Основные теоретические положения Если на вход электрической цепи с параллельным соединением активного сопротивления R, индуктивности L и емкости С (рис. 4.1) подается переменное синусоидальное напряжение  ,комплексное значение которого  ,то согласно первому закону Кирхгофа для мгновенных значений токов всех элементов в неразветвленной части цепи будет протекать ток  .Комплексные значения соответствующих величин  ,где 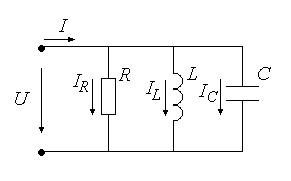   - соответственно активная, индуктивная и емкостная составляющие комплексной проводимости  .  Рис. 4.1. Векторную диаграмму (рис. 4.2) можно построить, рассматривая отдельные параллельные ветви этой цепи как независимые электрические цепи, включенные на одно напряжение. При построении исходим из того, что на резисторе R напряжение совпадает по фазе с током ( 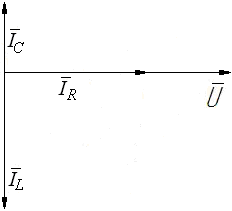 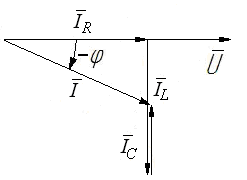), на индуктивности L напряжение опережает по фазе ток на угол  ( ), а на емкости С напряжение отстает по фазе от тока на угол ( ).  Рис. 4.2. Резонанс токов возникает в параллельной цепи, когда ток неразветвленной части схемы совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Полная проводимость рассматриваемой цепи  .Условие резонанса токов (BL=BC) можно записать через соответствующие параметры электрической цепи. Т.к. реактивная проводимость катушки, имеющей активное сопротивление Rk, определяется выражением  ,а проводимость конденсатора без учета его активного сопротивления (RС=0)  ,то условие резонанса может быть записано в виде  .Для явления резонанса токов характерно: 1. Полная проводимость всей цепи принимает минимальное значение равное активной составляющей при BL=BC.  .2. При минимальном значении проводимости ток неразветвленной части схемы имеет минимальное значение.  .3. Емкостный ток IС и индуктивная составляющая IL тока катушки IK равны по величине, а активная составляющая тока катушки IR равна току I, потребляемому из сети  ,  .4. Емкостный ток IС и индуктивная составляющая IL тока катушки могут во много раз превышать ток источника. 5.Реактивная составляющая полной мощности, потребляемой цепью, при BL=BC равна нулю:  .При этом индуктивная и емкостная составляющие реактивной мощности могут приобретать большие значения, оставаясь равными друг другу. 6. Полная мощность цепи равна активной составляющей  .7. Коэффициент мощности всей цепи  .8. Напряжение и ток электрической цепи при резонансе совпадают по фазе. Резонанс токов применяется в силовых электрических цепях для повышения коэффициента мощности (cosφ),т.к. это приводит к уменьшению тока в проводах, соединяющих потребитель с источником энергии, и полной мощности источника. Повышение коэффициента мощности обеспечивается подключением конденсаторов (или других источников реактивной емкостной мощности) параллельно потребителям электрической энергии, которые из-за свойственной им индуктивности имеют низкий коэффициент мощности. Кроме того, простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяют в радиоэлектронике в качестве колебательных контуров. Порядок выполнения работы. Собрать на рабочем поле экрана электрическую цепь синусоидального тока с параллельным соединением резистора, катушки и конденсатора (рис. 4.3). 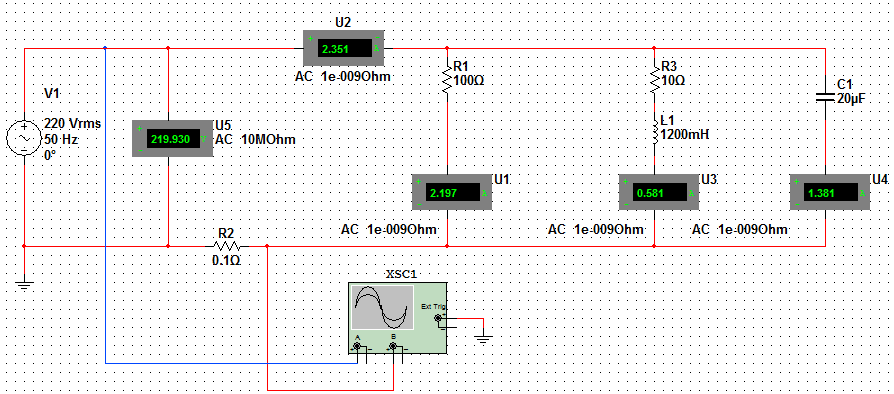 Рис. 4.3. Схема цепи с параллельным соединением резистора, катушки и конденсатора. Задать параметры элементов цепи согласно варианту (табл.4.1): Табл.4.1.
3. Заполнить таблицу согласно снятым показаниям приборов (табл.4.2). Рассчитать недостающие параметры. Построить векторную диаграмму для исследуемой цепи. Табл. 4.2.
Полная проводимость:  ;Активная проводимость ветви с резистором:  ;Активная проводимость ветви с индуктивностью: 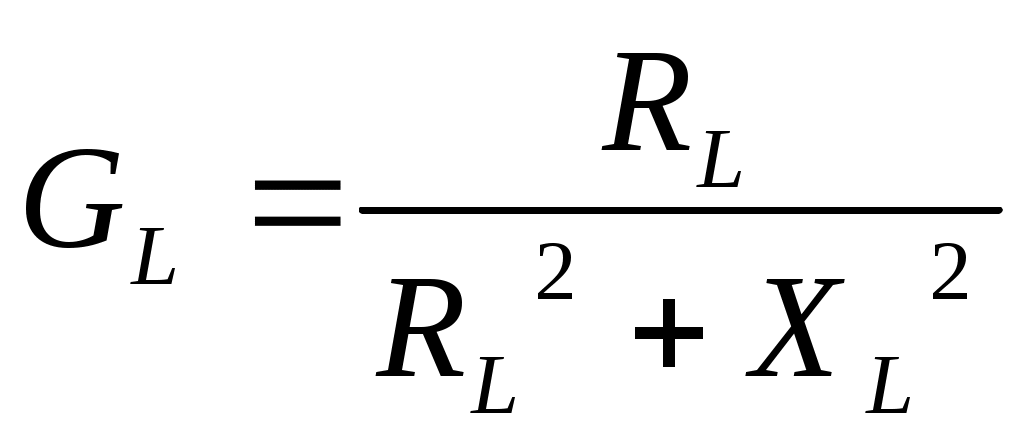 ;Активная проводимость ветви с конденсатором равна нулю. Реактивная проводимость ветви с резистором равна нулю. Реактивная проводимость ветви с индуктивностью: 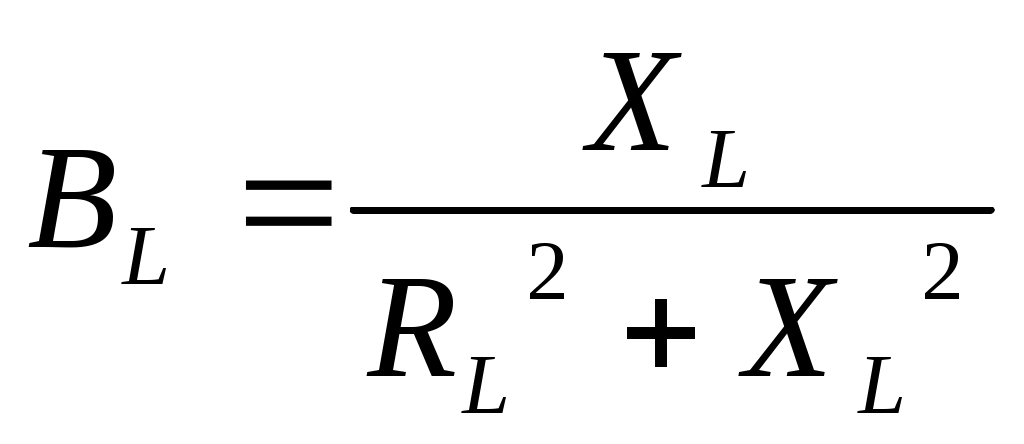 Реактивная проводимость ветви с конденсатором:  .Полная проводимость цепи в целом:  .Из треугольника проводимостей (рис. 4.4): 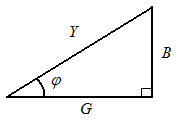  Рис. 4.4. Коэффициент мощности:  ;Угол сдвига фаз:  ;Из треугольника мощностей: 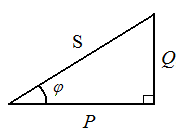 P= Scosφ; Q = Ssinφ,S= UI. Рис. 4.5. Построение векторной диаграммы целесообразно начать с построения вектора напряжения, так как при параллельном соединении элементов напряжение является общим для всех элементов. Согласно первому закону Кирхгофа ток в неразветвленной части цепи равен сумме токов, протекающим по элементам:  .Вектора токов строятся в масштабе, относительно вектора напряжения (рис. 4.6). 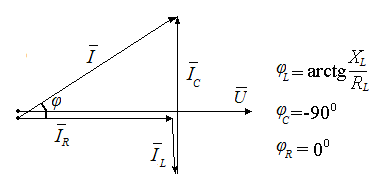 Рис. 4.6. 4. Согласно условию возникновения резонанса токов в цепи с параллельным соединением элементов: 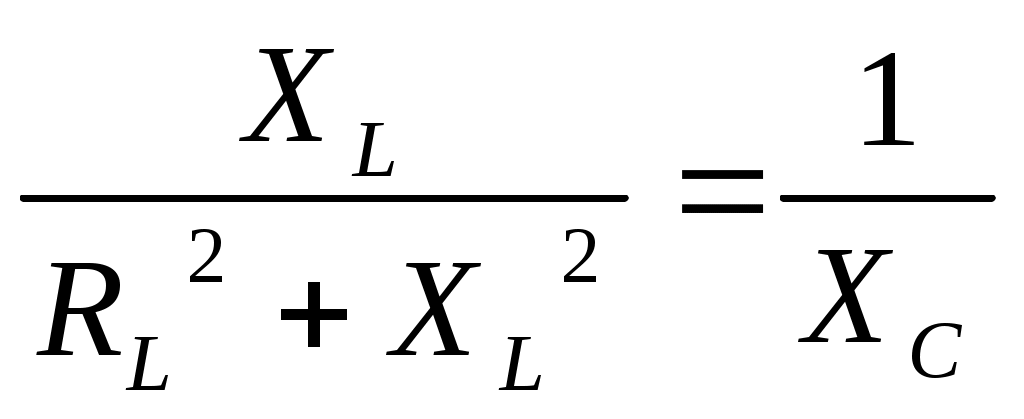 ; ;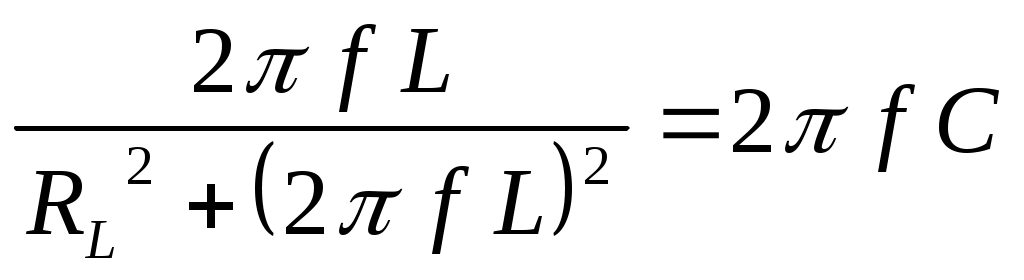 .Необходимо рассчитать значение частоты f0 питающего напряжения, при которой в цепи возникнет резонанс. Задать частоту напряжения источника, равную резонансной частоте f0. Снять показания приборов и заполнить таблицу. Построить векторную диаграмму цепи. 5. Рассчитать значение индуктивности, при которой в цепи возникнет резонанс. Задать индуктивность катушки, равную резонансному значению L0. Снять показания приборов и заполнить таблицу. Построить векторную диаграмму цепи. 6. Рассчитать значение емкости конденсатора, при которой в цепи возникнет резонанс Задать значение емкости конденсатора, равную резонансному значению С0. Снять показания приборов и заполнить таблицу. Построить векторную диаграмму цепи. Контрольные вопросы: 1. Каким образом осуществляется параллельное соединение элементов в электрической цепи? 2. Как определяются активная и реактивные проводимости? 3. Что такое резонанс токов? 4. Условия возникновения резонанса токов? 5. Изменением каких параметров электрической цепи можно обеспечить в ней режим резонанса токов? Дайте примеры практического использования резонансных явлений в электрических цепях. Лабораторная работа №5. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||