лабы. Лабораторные+работы+в+Multisim. Методические указания к выполнению лабораторных работ по электротехнике и основам электроники. 2011 Рассмотрены и рекомендован к изданию
 Скачать 1.71 Mb.
|
|
Исследование нелинейной электрической цепи постоянного тока. Цель работы: применение законов Ома и Кирхгофа для расчета разветвленных электрических цепей постоянного тока, снятие вольт-амперных характеристик для нелинейных элементов цени, использование графического метода расчета нелинейных электрических цепей постоянного тока. Основные теоретические положения. В отличие от линейных электрических цепей, при расчете нелинейных цепей, параметры которых зависят от тока и напряжения и имеют криволинейные характеристики, удобно пользоваться графическим методом с использованием экспериментальных вольт-амперных характеристик элементов цепи, т.е. зависимостей тока в цепи от напряжения на элементах цепи I=f(U). На рис.2.1 представлена схема последовательного, а на рис.2.2 - параллельного соединений линейного элемента - резистора Rи нелинейного элемента - полупроводникового диода Д, вольт-амперные характеристики которых приведены на рис.2.3 и 2.4. 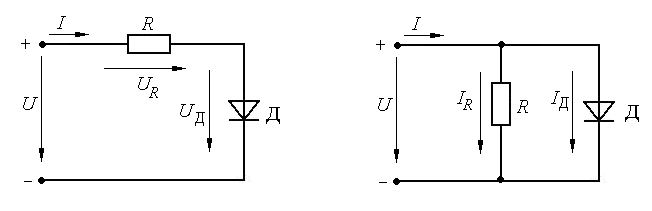 Рис. 2.1. Рис. 2.2. Так как при последовательном соединении элементов ток обоих участков цепи одинаков, а подведенное напряжение  определение зависимости тока на входе от значения приложенного напряжения производят суммированием абсцисс заданных кривых (напряжений) при заданном значении тока I(рис. 2.3).При параллельном соединении элементов цепи указанную зависимость находят суммированием соответствующих токов 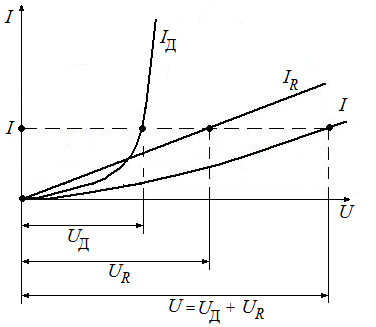 при заданном значении напряжения U(рис. 2.4). Рис. 2.3. 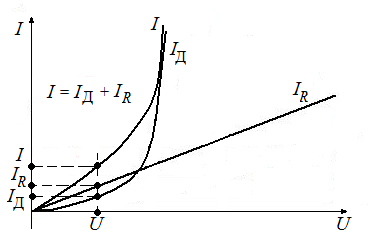 Рис. 2.4. Аналогично находят остальные координаты результирующих вольт-амперных характеристик цепи путем изменения значений I и U. Методические указания по выполнению работы. 1. Собрать схему электрической цепи – последовательное соединение линейного элемента – резистора и нелинейного – диода (рис. 2.5.). Задать величину сопротивление резистора 10 Ом. 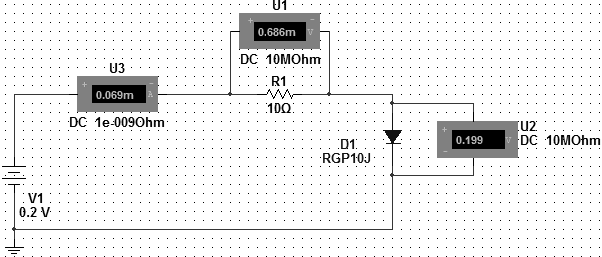 Рис. 2.5. Схема цепи. Изменяя значения напряжения источника в заданном диапазоне, снять показания приборов, записать их в таблицу 2.1. Отобразить зависимость тока цепи от величины напряжения на резисторе, величины напряжения на диоде и величины напряжения источника ЭДС. Табл. 2.1.
2. Собрать схему электрической цепи – параллельное соединение линейного элемента – резистора и нелинейного – диода (рис. 2.6). Сопротивление резистора – 10 Ом. 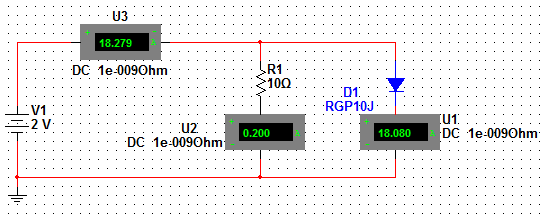 Рис. 2.6. Схема цепи. Изменяя значения напряжения источника в заданном диапазоне, снять показания приборов, записать их в таблицу 2.2. Отобразить зависимости тока на резисторе, тока на диоде и тока в неразветвленной части цепи от величины напряжения источника ЭДС. Табл. 2.2.
Контрольные вопросы. 1. Дайте определения линейных и нелинейных элементов электрической цепи. 2. Какие цепи считают линейными, а какие – нелинейными? 3. Приведите пример линейного элемента и его вольт-амперную характеристику. 4. Приведите пример нелинейного элемента и его вольт-амперную характеристику. 5. Выполняются ли законы Ома и Кирхгофа для нелинейных цепей? Лабораторная работа №3. Последовательное соединение резистора, катушки и конденсатора в цепи переменного тока. Цель работы: опытным путем проверить основные законы для цепи переменного тока с последовательным соединением приемников электрической энергии: резистора, катушки индуктивности и конденсатора. Основные теоретические положения. Если на вход электрической цепи с последовательно соединенными активным сопротивлением R, индуктивностью L и емкостью С (рис. 3.1) подается подать переменное синусоидальное напряжение 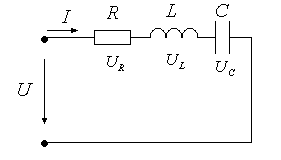 , Рис.3.1. комплексное значение которого  ,то по цепи будет протекать ток  ,комплексное значение которого  .Согласно второму закону Кирхгофа в комплексной форме записи напряжение, подводимое к этой электрической цепи, может быть записано  ,где   ,  - комплексные напряжения на участках цепи. Причем XL=ωLи Хс=1/ωС - индуктивное и емкостное сопротивления; ω=2πf- угловая частота; f - частота напряжения. Если комплексы напряжений активного, индуктивного и емкостного участков цепи заменить произведениями комплексов тока и сопротивления, то уравнение для подводимого к электрической цепи комплексного напряжения преобразуется к виду  или к виду уравнения, записанного в комплексной форме по закону Ома для всей цепи:  ,где  - полное комплексное сопротивление электрической цепи переменного тока.Модуль полного комплексного сопротивления цепи переменного тока  ,а аргумент  ,есть угол между векторами напряжения и тока, определяемый как разность начальных фаз соответственно  .С учетом того, что на резисторе R напряжение совпадает по фазе с током ( 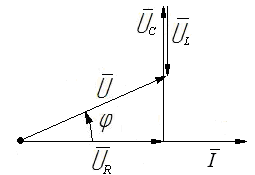 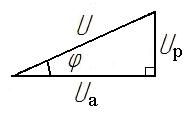), на индуктивности L напряжение опережает ток на угол  ( ), а на емкости С напряжение отстает от тока на ( ), построенная векторная диаграмма для электрической цепи (рис. 3.1) представлена на рис. 3.2.  Рис. 3.2. Взаимосвязь между действующими значениями тока и напряжения и полным сопротивлением цепи определяется соотношениями U=zIили I=U/z, где действующие значения напряжения  и тока  .Из треугольника напряжений на векторной диаграмме (рис. 3.2), можно получить треугольник сопротивлений (рис. 3.3) для рассматриваемой цепи, разделив стороны этого треугольника на комплексный ток  , из которого следует, что  ; ,а также треугольник мощностей (рис. 3.4), умножив стороны треугольника сопротивлений на квадрат тока в цепи I2. 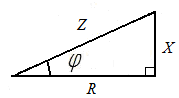 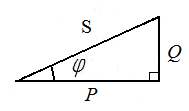 Рис. 3.3. Рис. 3.4. Активная мощность цепи переменного тока  , отсюда  .Из треугольника мощностей можно установить взаимосвязь между активной Р,полной Sи реактивной Qмощностями электрической цепи:  , , .При этом реактивная составляющая полной мощности цепи находится как разность реактивной индуктивной QL. и реактивной емкостной QCсоставляющих:  .Выражения для полной мощности цепи переменного тока в комплексной форме записывают в следующем виде:  или  ,где 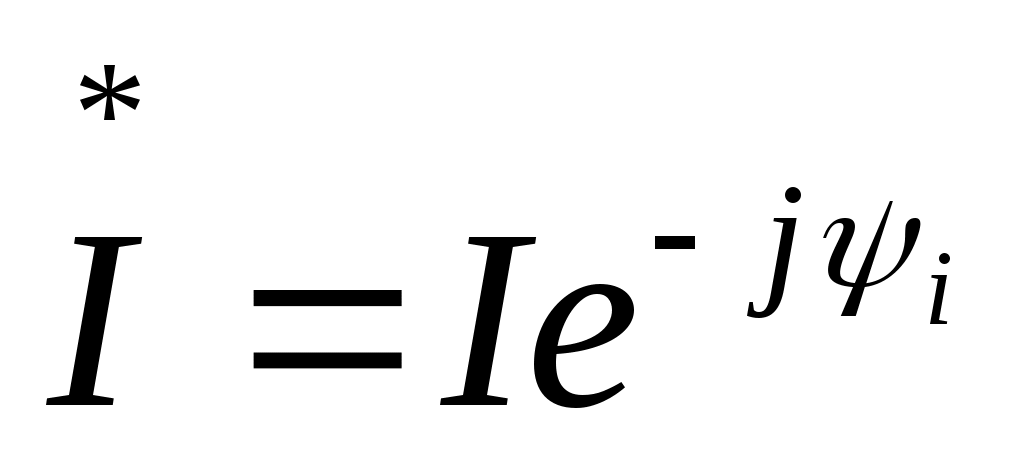 - сопряженное значение комплексного тока  .Полученные выражения показывают, что угол сдвига фаз между током и напряжением  питающей сети зависит от характера сопротивлений, включенных в цепь переменного тока. При этом если , т.е.  – характер нагрузки индуктивный, , т.е.  – характер нагрузки емкостной.Однако возможно особое состояние цепи переменного тока при последовательном включении активного сопротивления R, индуктивности Lи емкости С, при котором индуктивное сопротивление цепи равно емкостному сопротивлению  . , т.е.  - характер нагрузки чисто активный.Это явление в неразветвленной электрической цепи переменного тока называется резонансом напряжений. Условием для возникновения резонанса является равенство реактивных сопротивлений и равенство нулю разности фаз тока и напряжения на входе цепи  . Частота, на которой возникнет равенство реактивных сопротивлений, называется резонансной и определяется как  .В простейшем случае резонанс напряжений может быть получен в электрической цепи при последовательном включении катушки индуктивности и конденсаторов за счет изменения емкости конденсаторов при постоянных параметрах катушки. Значения частоты, индуктивности, напряжения и активного сопротивления цепи неизменны. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 3.5. 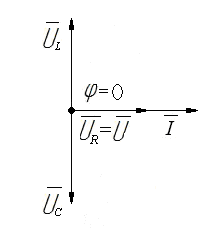 Рис. 3.5. Реактивная составляющая напряжения UL. на катушке при резонансе равна напряжению UС на конденсаторе, напряжение источника U приложено к активному сопротивлению R. Точка резонанса в этих условиях определяется по наибольшему значению тока в электрической цепи. Для резонанса напряжений характерно: 1. Полное сопротивление электрической цепи переменного тока минимально и равно ее активному сопротивлению, т.е.  , так как XL = XС.2. При неизменном напряжении питающей сети (U=const) ток в цепи достигает наибольшего значения I=U/z=U/R. 3. Коэффициент мощности cos φ=cos(ψu–ψi)=P/S=R/z=R/R=1, т.е. максимальный, (соответствующий ). Это значит, что вектор тока и вектор напряжения сети совпадают по направлению, т.к. имеют равные начальные фазы ψi= ψu.4. Активная мощность  имеет наибольшее значение, равное полной мощности S, а реактивная мощность цепи  равна нулю  .Однако реактивная индуктивная и реактивная емкостная составляющие полной мощности  могут приобретать большие значения, в зависимости от значений тока и реактивных сопротивлений.5. Напряжения на емкости и индуктивности равны  и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. 6. Напряжение на активном сопротивлении равно напряжению питающей сети, т.е.  .При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и перенапряжения на отдельных ее участках. Поэтому, резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, т.к. может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов. В то же время резонанс напряжений широко используется в радиотехнике и электронике для выделения сигналов заданной частоты. Методические указания по выполнению работы. 1. Собрать на рабочем поле экрана электрическую цепь синусоидального тока с последовательным соединением резистора, катушки и конденсатора (рис. 3.6). Катушка индуктивности является реальной, поэтому она обладает активным сопротивлением обмотки. 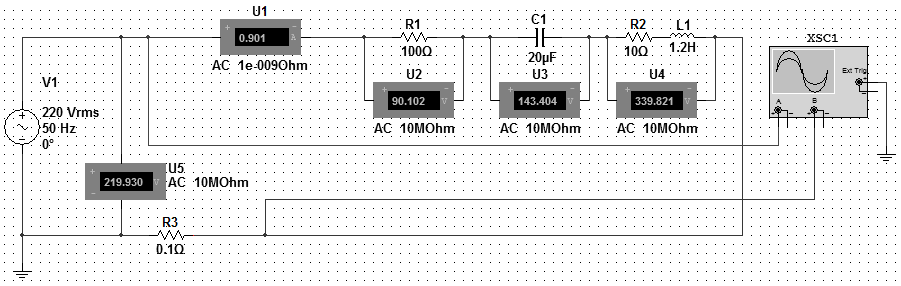 Рис. 3.6. Схема цепи с последовательным соединением резистора, катушки и конденсатора. Элементы электрической цепи берутся из окон выбора источников и компонентов. Измерительные приборы – с верхней панели индикаторов, осциллограф – из боковой панели инструментов. Измерительные приборы (амперметр и вольтметр) необходимо переключить в режим измерения переменного тока АС. Для соединения элементов схемы необходимо подвести курсор к подсоединяемому концу одного элемента до появления точки на конце этого элемента, нажать левую кнопку мыши, подвести линию – «провод» к началу следующего элемента до появления точки, снова нажать левую кнопку мыши. 2. Задать параметры элементов цепи согласно варианту (табл.3.1). Табл.3.1.
Провод, идущий на канал «А» осциллографа, необходимо обозначить красным цветом, подведя курсор к проводу, и, нажав, правую кнопку мыши, затем «Color Segment» (рис. 3.7), выбрать цвет (красный).  Рис. 3.7. В ключить цепь, нажав клавишу (положение «I») в правом верхнем углу монитора. После появления показаний приборов выключить цепь, нажав ту же клавишу (положение «0»). Для наблюдения осциллограмм напряжения и тока необходимо активизировать осциллограф двойным нажатием левой кнопки мыши. Можно расширить осциллограф, растянув его погоризонтали и вертикали. В случае необходимости настроить осциллограф: горизонтальная развертка регулируется кнопками «Time base» (рис. 3.7), при этом изображение сжимается или расширяется по горизонтали (по оси времени).  Рис. 3.8. Масштаб синусоид устанавливается заданием цены деления по вертикальной оси «V/div» (рис. 3.8).  Рис. 3.9. На канале «А» отображается синусоида напряжения (красная), на канале «В» – синусоида тока (черная). С помощью осциллографа можно измерить угол сдвига фаз между напряжением и током цепи. Для измерения угла сдвига фаз φ между напряжением и током необходимо подвести красный курсор к началу синусоиды напряжения (красная синусоида), а синий – к началу синусоиды тока (черная синусоида). В правом окне осциллографа (рис. 3.9.) значение (Т2 – Т1) необходимо перевести в градусы:  ,где f – частота напряжения источника питания, Гц.  Рис. 3.10. Обязательно обратить внимание на знак угла φ. 3. Заполнить таблицу согласно снятым показаниям приборов (табл.3.2). Рассчитать недостающие параметры. Табл. 3.2
Полное сопротивление цепи:  ;Индуктивное сопротивление катушки: XL = 2πfL; Емкостное сопротивление конденсатора: XC =  ;Из треугольника сопротивлений:  Коэффициент мощности:  ;Угол сдвига фаз:  ;Из треугольника мощностей: P = Scosφ; Q = Ssinφ, S = UI. 4. Построить векторную диаграмму цепи. Построение векторной диаграммы целесообразно начать с построения вектора тока, так как при последовательном соединении элементов ток в цепи является общим для всех элементов. Согласно второму закону Кирхгофа напряжение источника равно сумме падений напряжений на приемниках:  .Вектора напряжений строятся в масштабе, относительно вектора тока (рис. 3.8). Обходя цепь по выбранному направлению, следует откладывать вектор падения напряжения на каждом отдельном участке в направлении по отношению к вектору тока, соответствующем характеру нагрузки элемента. 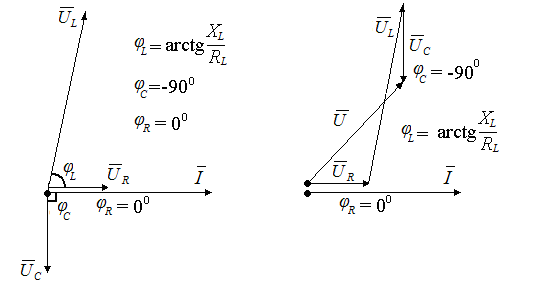 Рис. 3.11. 5. Рассчитать значение частоты питающего напряжения, при которой в цепи возникнет резонанс:  .Задать частоту напряжения источника, равную резонансной частоте f0. Снять показания приборов и заполнить таблицу. Построить векторную диаграмму цепи. 6. Рассчитать значение индуктивности, при которой в цепи возникнет резонанс:  .Задать индуктивность катушки, равную резонансному значению L0. Снять показания приборов и заполнить таблицу. Построить векторную диаграмму цепи. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||