лабы. Лабораторные+работы+в+Multisim. Методические указания к выполнению лабораторных работ по электротехнике и основам электроники. 2011 Рассмотрены и рекомендован к изданию
 Скачать 1.71 Mb.
|
|
Соединение фаз приемника по схеме «треугольник». Цель работы: исследовать режимы работы трехфазного приемника, фазы которого соединены по схеме «треугольник»: симметричный, несимметричный, обрыв фазы, обрыв двух фаз, обрыв линейного провода. Проверить соотношения между линейными и фазными токами при симметричном и несимметричных режимах. Основные теоретические положения При соединении трехфазного потребителя электрической энергии треугольником каждая фаза потребителя присоединяется соответственно к двум линейным проводам, поэтому фазные напряжения оказываются равными соответствующим линейным напряжениям Uф = Uл, а фазные токи неравны линейным, т.к. в начале каждой фазы потребителя имеется узел разветвления токов. Для каждого узла по первому закону Кирхгофа:  , , .Соотношения между фазными напряжениями, токами и сопротивлениями по закону Ома  ,  ;  .Углы сдвига по фазе между векторами фазных напряжений,  ,  ,  и соответствующих фазных токов  ,  ,  определяются фазными сопротивлениями потребителя  , , .В случае симметричной нагрузки сопротивления фаз равны  . При этом равны как активные, так и реактивные сопротивления фаз потребителя  ,  , причем реактивные сопротивления имеют одинаковый (индуктивный или емкостный) характер. Фазные токи и соответствующие углы сдвига по фазе между фазными напряжениями и фазными токами будут равны между собой: = = = ,  = = = .Из векторной диаграммы для случая симметричной активной нагрузки при соединении треугольником (рис. 5.6), видно, что линейные токи равны. При этом фазные и линейные токи соотносятся 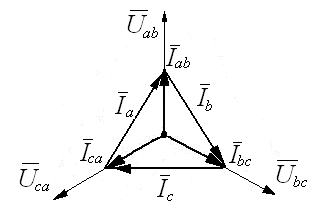 . Рис. 6.1. При несимметричной нагрузке (рис. 5.7) фазные токи неодинаковые. Линейные токи определяются как разности фазных токов. 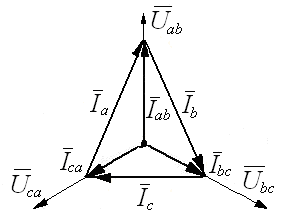 Рис. 6.2. Активная мощность трехфазного потребителя электроэнергии при несимметричной нагрузке равна сумме активных мощностей всех его фаз: - при соединении звездой  ;- при соединении треугольником  .Аналогично полную и реактивную мощности трехфазного потребителя в случае несимметричной нагрузки можно найти как суммы полных и реактивных мощностей отдельных фаз потребителя - при соединении звездой  ; ;- при соединении треугольником  ; .При симметричной нагрузке активная мощность трехфазного потребителя независимо от схемы его соединения может быть найдена как  или  .Аналогично реактивная мощность трехфазного потребителя при симметричной нагрузке:  Или  .Полная мощность трехфазного потребителя при симметричной нагрузке:  или  .Порядок выполнения работы. 1. Собрать на рабочем поле экрана электрическую цепь синусоидального тока с соединением фаз приемника по схеме «треугольник» (рис.6.3). 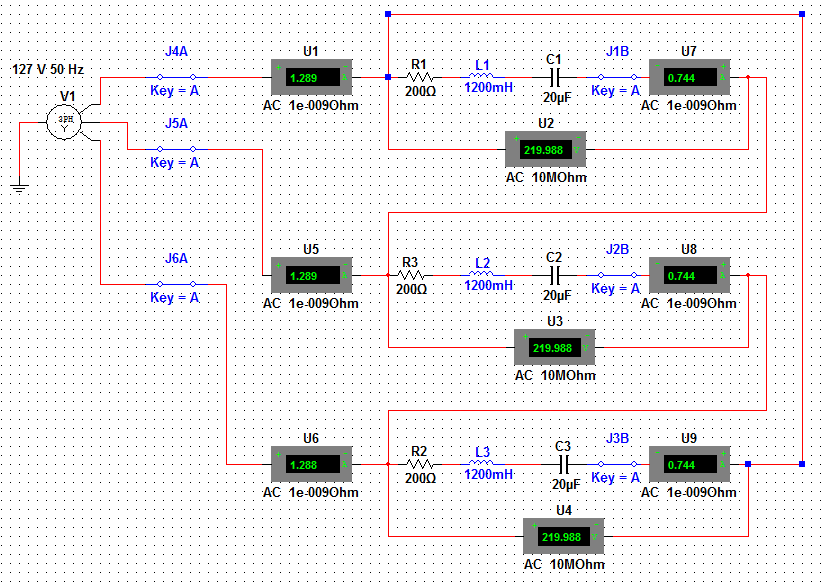 Рис. 6.3. Схема цепи с соединением фаз приемника по схеме «треугольник». Задать параметры элементов цепи согласно варианту (табл. 4.1): Табл. 6.1.
3. Провести опыт при симметричном режиме приемника. Снять показания приборов. Результаты измерений записать в табл. 4.2. 4. Оборвать одну из фаз. Снять показания приборов. Результаты измерений записать в табл. 4.2. 5. Оборвать две фазы. Снять показания приборов. Результаты измерений записать в табл. 4.2. 6. Оборвать линейный провод. Снять показания приборов. Результаты измерений записать в табл. 4.2. 7. Уменьшить параметры элементов в первой фазе в четыре раза, во второй фазе – в два раза. Снять показания приборов. Результаты измерений записать в табл. 4.2. Табл.6.2.
8. По результатам измерений построить векторные диаграммы для каждого опыта. Величины фазных напряжений Uab, Ubc, Ucaне зависят от режима работы трехфазного приемника. Построение векторных диаграмм целесообразно начинать с построения векторов фазных напряжений. Вектора фазных напряжений строятся согласно масштабу. Вектора фазных токов строятся относительно соответствующих фазных напряжений. Углы сдвига фаз φab, φbc, φca между фазными напряжениями и токами определяются по формулам:  ;  ; ,где  ;  .При построении векторов токов необходимо учитывать знак угла сдвига фаз. Вектора линейных токов строятся согласно выражениям:  a = ab – bc; b = bc – ca; c = ca – bc.Для случая, рассмотренного на рис. 6.3 векторная диаграмма для симметричной нагрузки имеет вид (табл. 6.3): Rаb = Rbc = Rca = 200 Ом, Lаb = Lbc = Lca = 1200 мГн, где  = 2·3,14·50·1200·103 = 377 Ом;Cаb = Cbc = Cca = 20 мкФ, где 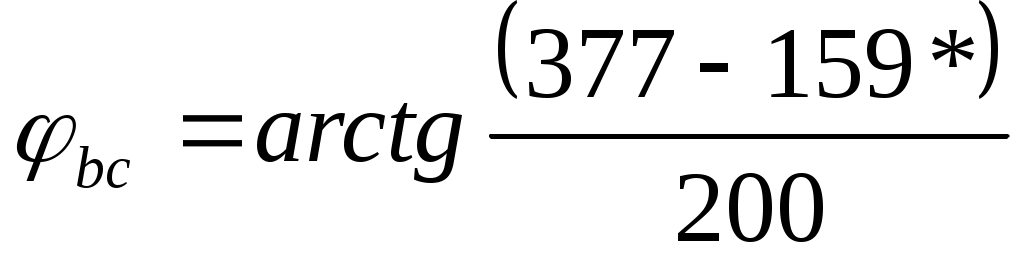=  = 159 Ом. =  = 470; = = 470; =  = 470.Табл. 6.3.
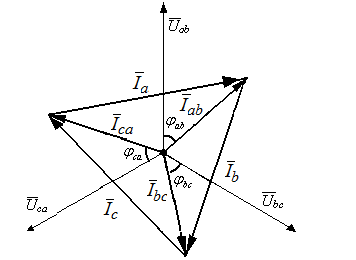 Рис. 6.4. Для несимметричной нагрузки векторная диаграмма имеет вид (табл. 4.4): Rаb = 50 Ом, Lаb = 300 Гн, Cаb = 5 мкФ; (XL = 31 Ом, XC = 640 Ом); Rbc = 100, Lbc = 600 Гн, Cbc = 10 мкФ; (XL = 188 Ом, XC = 318 Ом); Rca = 200 Ом, Lca = 1200 Гн, Cca = 20 мкФ; (XL = 377 Ом, XC = 159 Ом). Табл. 4.4.
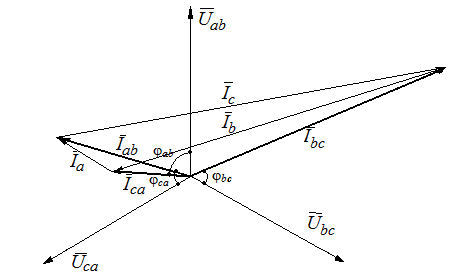=  = - 850; = = - 520; = = 470. Рис. 6.5. Контрольные вопросы. 1. Каким образом осуществляется схема соединения фаз потребителя по схеме «треугольник»? 2. Каково соотношение между линейными и фазными напряжениями симметричного приемника, фазы которого соединены по схеме «треугольник»? 3. Каково соотношение между линейными и фазными токами при соединении приемника по схеме «треугольник»? 4. Как вычислить активную, реактивную и полную мощности симметричной трехфазной нагрузки? 5. Как вычислить активную, реактивную и полную мощности несимметричной трехфазной нагрузки? Лабораторная работа № 7. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||