матлогика_методичка. Методические указания к выполнению практических работ Омск Издательство Омгту 2009
 Скачать 0.58 Mb.
|
Тема 4. НЕЧЕТКАЯ ЛОГИКАНечеткая логика отличается от двузначной классической логики тем, что если значения истинности высказывания классической логики могут быть только 0 («ложь») и 1 («истина»), то нечеткая логика допускает несчетное число промежуточных истинностных значений для высказываний в интервале [0, 1]. При описании сложных систем, в которых наряду с количественными данными присутствуют неоднозначные качественные данные, приходится использовать нечеткие понятия и рассуждения. Для формализации таких задач Л. Заде разработал основы математического аппарата, опирающегося на понятия нечетких множеств и нечеткой логики. 4.1 Основные понятия нечетких множествПусть М – некоторое множество, рассмотрим какое-либо подмножество А этого множества. Для любого хМ имеем хА или хА. Можно ввести характеристическую функцию подмножества А: 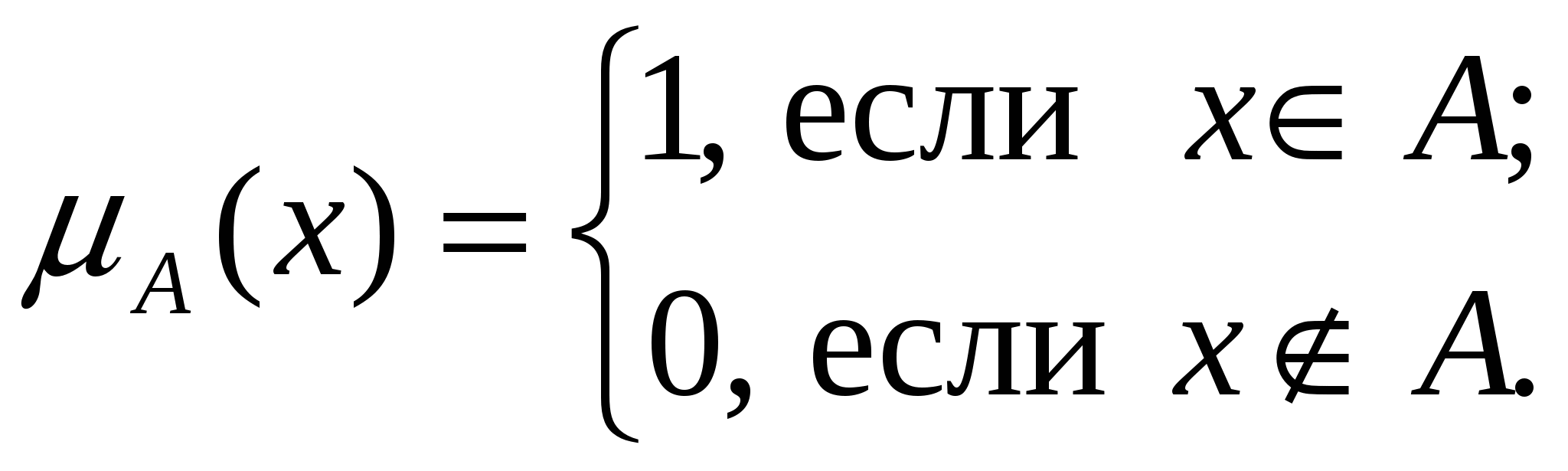 Тогда, например, если M={a, b, c, d, e, f, g, h}иA={a, b, c, d}, имеем:
Для универсального множества М:х M (x) = 1. Множества, для которых характеристическая функция принимает только значения 0 или 1, будем называть четкими. Классическая логика оперирует с четкими множествами. Для нечетких множеств характеристическая функция может принимать любые значения из интервала [0,1]. Например,
Для записи нечетких множеств используется обозначение: А={(х, A (х))| xM}. Запись  характеризует степень принадлежности элемента x множеству A.Для нечетких множеств определены отношение включения () и равенства (=): АВ тогда и только тогда, когда xM: A (х) B (х); А=В тогда и только тогда, когда xM: A (х) =B (х). Над нечеткими множествами выполняются операции: Дополнение А:  Пересечение:  Объединение:  АВ={(х, max {A (х), B (х)})| xM }. |