матлогика_методичка. Методические указания к выполнению практических работ Омск Издательство Омгту 2009
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
5.2. Машина ТьюрингаМашина Тьюринга – абстрактная машина, математическая модель идеализированного вычислительного устройства. Машина Тьюринга полностью определяется: а) внешним алфавитом A = {a0, a1,... an}, где a0 – символ пустой ячейки; б) алфавитом внутренних состояний Q = {q0, q1,...qm}, где q0 – состояние остановки: попав в него машина прекращает работу; q1– начальное состояние: в этом состоянии машина начинает работать; в) программой, т.е. совокупностью команд T(i,j) (i=1, …, m;j=0,1,…,n),каждая из которых имеет вид: ajqiarSqk, где S – предписание лентопротяжному механизму машины (сдвиг), S = L, если сдвиг влево, S = R, если сдвиг вправо, S = C, если каретка остается на месте. Условие однозначности требует, чтобы для любого j и любого i имелась только одна команда указанного вида. Машина Тьюринга состоит из ленты и управляющего устройства (УУ) со считывающей и записывающей головкой (кареткой) (рис. 5.1). УУ 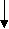
Рис. 5.1. Схема машины Тьюринга Лента жестко закреплена слева и бесконечна справа. Иногда считают, что лента не ограничена справа и слева. Лента разделена на ячейки, которые нумеруются натуральными числами. В каждую ячейку ленты заносятся символы внешнего алфавита машины Тьюринга. Головка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, то стоит против некоторой ячейки ленты; говорят, что головка обозревает эту ячейку. За единицу времени (шаг) головка может сдвинуться на одну ячейку влево или вправо. Головка может распознать содержимое обозреваемой ячейки, заносить символ внешнего алфавита в текущую ячейку и стирать содержимое текущей ячейки (записывать туда пробел). Управляющее устройство может находиться в одном из множества дискретных состояний. Словом называется последовательность P = ai1, ai2, … , ais символов, записанных в ячейках ленты, где ai1 – символ, находящийся в самой левой непустой ячейке, а ais – символ, находящийся в самой правой непустой ячейке. Количество символов в слове называется длиной слова. Пусть в некоторый момент времени t на ленте записано слово P, управляющее устройство находится в состоянии qi, а каретка – напротив символа aimслова P. Конфигурацией машины в момент времени t называется последовательность K = ai1, … , ai(m – 1), qi, aim … , ais. Конфигурации в начале и в конце работы называют соответственно начальной и заключительной. Пример 5.1. Машина с внешним алфавитом A = {1, a}, алфавитом внутренних состояний Q = {q1, q2} и программой 1q11Rq1, aq11R q1, из любой начальной конфигурации будет работать бесконечно, заполняя единицами всю ленту вправо от начальной точки. Порядок работы машины Тьюринга задается в виде таблицы. В каждый столбец верхней строчки заносятся символы внутреннего алфавита, в каждую строчку первого столбца – символы внешнего алфавита. В ячейках на пересечении других столбцов и строчек помещаются команды. Если на пересечении какой-либо строки и какого-либо столбца получим пустую клетку, то это означает, что в данном внутреннем состоянии данный символ встретиться не может. Таблица 5.1
Формат команды: aSq, где a – новое содержимое текущей ячейки (символ внешнего алфавита, который заносится в ячейку); S – команда лентопротяжному механизму (влево, вправо, стоп); q – новое внутреннее состояние машины Тьюринга. Работа машины на основании заданной программы происходит следующим образом. Предположим, что в данный момент времени машина Тьюринга находится во внутреннем состоянии qi, а в обозреваемой головкой ячейке ленты находится символ aj. Тогда машина переходит к выполнению команды arSqk в ячейке, на пересечении столбца qi и строки aj: 1) в текущую ячейку ленты заносится новый символ ar ; 2) происходит сдвиг головки влево (S = L), или сдвиг головки вправо (S = R), или головка остается неподвижной (S = C); 3) машина переходит в новое внутреннее состояние qk. Возможные случаи останова машины Тьюринга: 1) в ходе выполнения программы машина дойдет до выполнения команды остановки; программа считается выполненной (результативная остановка); 2) машина никогда не останавливается, происходит зацикливание. Данные машины Тьюринга – это слова во внешнем алфавите ленты. На ленте записывается и исходные данные, и конечный результат. На ленте могут быть записаны последовательности слов. Между словами ставится специальный символ – разделитель, пробел или, например, символ . Натуральное число a представляется словом 1…1= 1a, состоящим из a единиц. Например, числу 3 соответствует слово 111. Пример 5.2. Построить машину Тьюринга, которая производит сложение двух натуральных чисел a и b. Сложить два числа a и b – значит слово 1a 1b преобразовать в слово 1 a+b. Это можно сделать, удалив в записи ab символ разделителя и сдвинув первое слагаемое ко второму. Такая машина может быть задана таблицей 5.2. Внешний алфавит A = {1, , _}, где – символ разделителя, а _ – символ пустой ячейки (пробела). Множество внутренних состояний состоит из трех состояний Q = {q0, q1, q2}. Таблица 5.2
Начальное и конечное состояния ленты для случая a = 5, b = 3 представлено на рис. 5.2 a и б. a 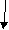 ) )
б 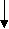 ) )
Рис. 5.2. Схема машины Тьюринга, выполняющей сложение двух натуральных чисел 5.3. ЗаданияПостройте машину Тьюринга, которая заданное входное слово P преобразует в выходное слово R. В начальном положении обозревается крайняя левая ячейка на ленте. Варианты индивидуальных заданий
Список литературы
Редактор Л.И. Чигвинцева Компьютерная верстка О.Г. Белименко ИД № 06039 от 12.10.2001 Свод. темплан 2009 г. Подписано в печать 11.09.09. Формат 60х84 1/16. Отпечатано на дупликаторе. Бумага офсетная. Усл. печ. л. 2,5. Уч.-изд. л. 2,5. Тираж 200 экз. Заказ 601.  Издательство ОмГТУ. Омск, пр. Мира, 11. Т. 23-02-12 Типография ОмГТУ |
