Методы контроля. Методические указания мук 116702 ббк 51. 21

• Название: Методические указания мук 116702 ббк 51. 21
• Анкор: Методы контроля
• Дата: 06.09.2022
• Размер: 1.49 Mb.
• Имя файла: Методы контроля.doc
• Тип: Методические указания; #664072
• страница: 2 из 8

Расчет плотности потока энергии в области II. В области II поле обусловлено дифракцией электромагнитных волн на кромке параболического зеркала. Однако область II имеет три характерных подобласти (рис.2.5), которые образуются после проведения двух касательных (1 и 2) в точках А и Б. Из подобласти II-а видна вся кромка антенны, из подобласти II-б видна часть кромки, из подобласти II-в кромка вообще не видна.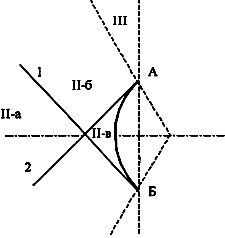


Рис.2.5. К расчету ППЭ в области II.
Исходными данными для расчета являются следующее параметры радиосредства: мощность излучения P, Вт; длина волны , м; диаметр антенны d, м; половина угла раскрыва зеркала ₀; коэффициент использования поверхности зеркала k_ип;  - уровень напряженности электрического поля на кромке зеркала. Постановка задачи иллюстрируется на рис.2.6.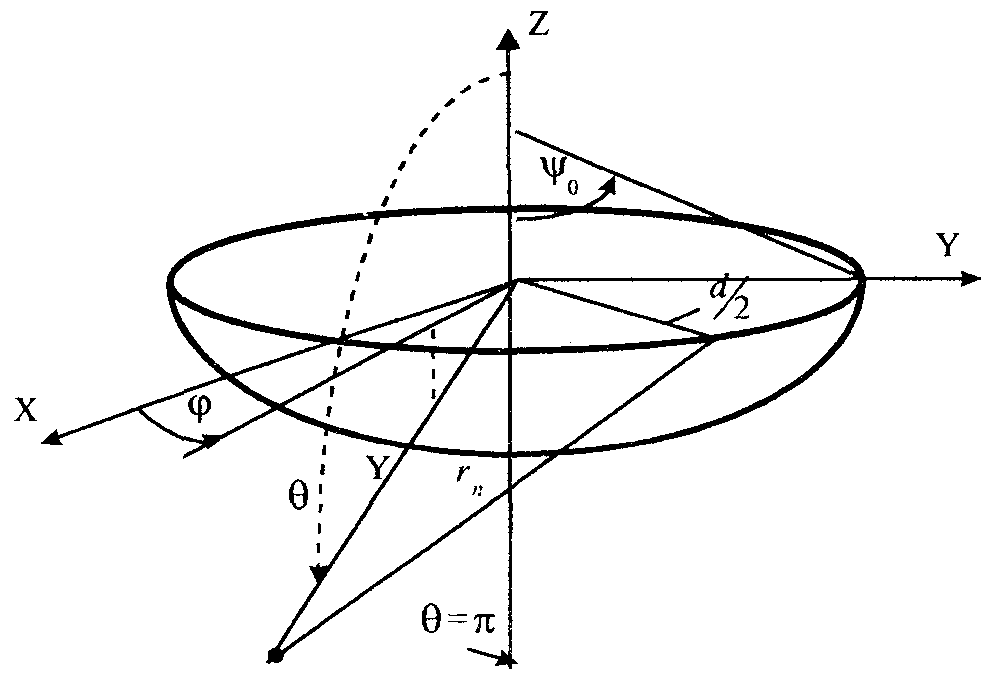


Рис.2.6. К расчету ППЭ методом ГТД.
Сферические составляющие напряженности электрического поля в подобласти II-а имеют вид:

; (2.27)

Последовательность расчетов при использовании метода геометрической теории дифракции (ГТД) следующая:

1. Определяется ряд вспомогательных величин:

;

;

;

sign _1,2 (sign  = 1, если   1, sign  = -1, если  < 1);



2. Вычисляются функции: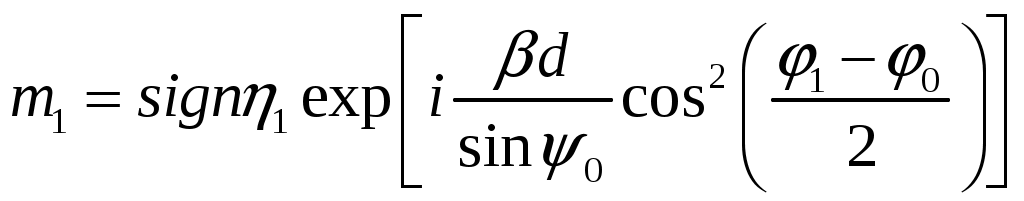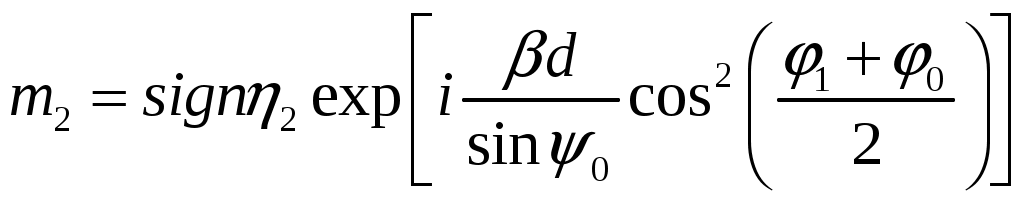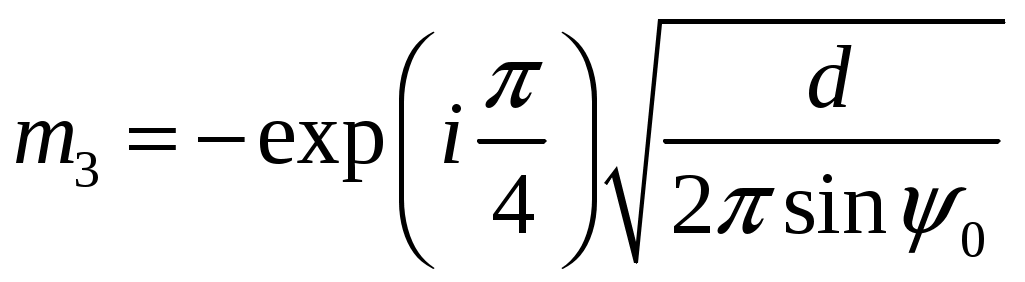

;

;

(2.28)

3. Вычисляются специальные функции - интегралы Френеля:

, (2.29)

в кото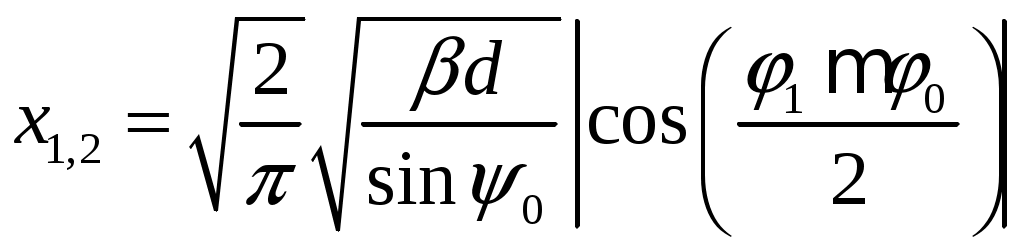рых

, (2.30)

- косинус интеграла Френеля,

- синус интеграла Френеля. (2.31)

4. Рассчитываются коэффициенты дифракции:

; (2.32)

5. Рассчитываются некоторые функции, определяющие дифракцию первичного поля облучателя на кромке зеркала:

,

(2.33)

В этих выражениях r_n - расстояние от произвольного элемента кромки ds до расчетной точки: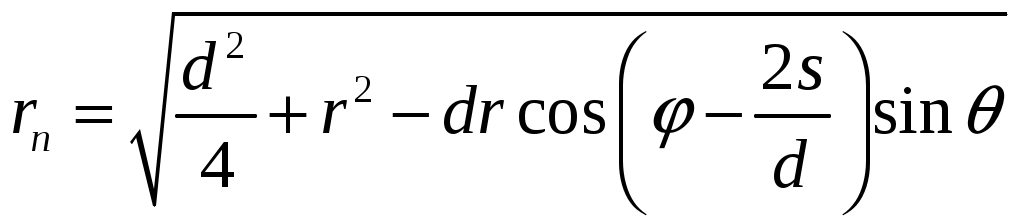

, где (2.34)

r - расстояние от центра апертуры до расчетной точки (рис.2.6).

6. Определяется усредненное значение ППЭ в центре апертуры:

, мкВт/см² (2.35)

7. Определяется значение напряженности поля в центре апертуры:

, В/м (2.36)

8. Рассчитываются сферические компоненты дифракционного поля E_, E_ по формулам:

; , (2.37)

где  = 0,316 уровень поля на ребре кромки.

9. Определяются составляющие ППЭ, обусловленные дифракционными компонентами поля E_, E_ по формулам: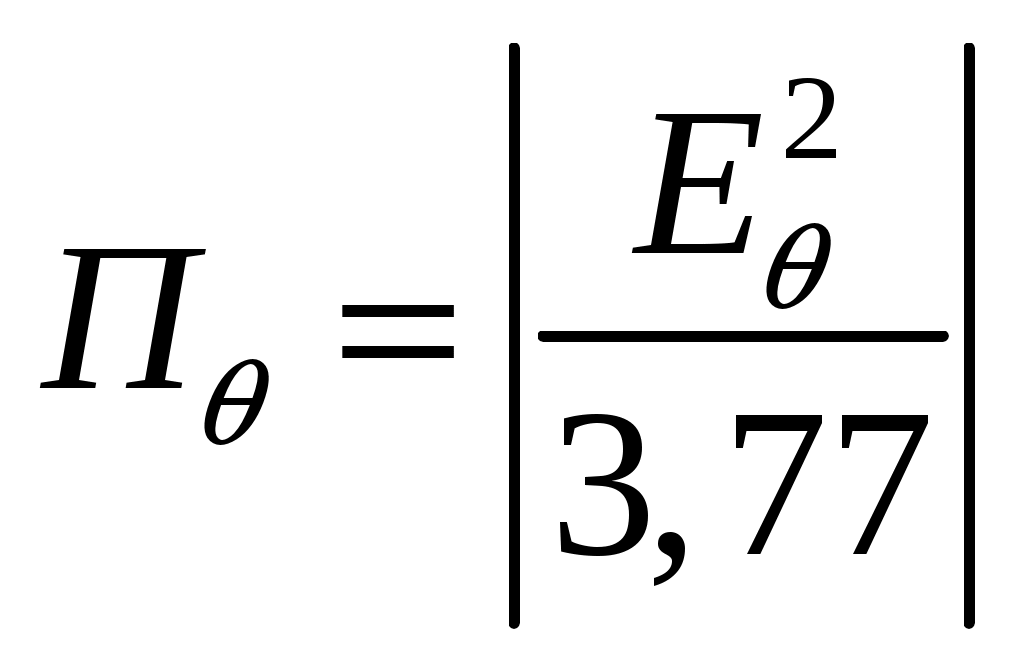

, мкВт/см²; 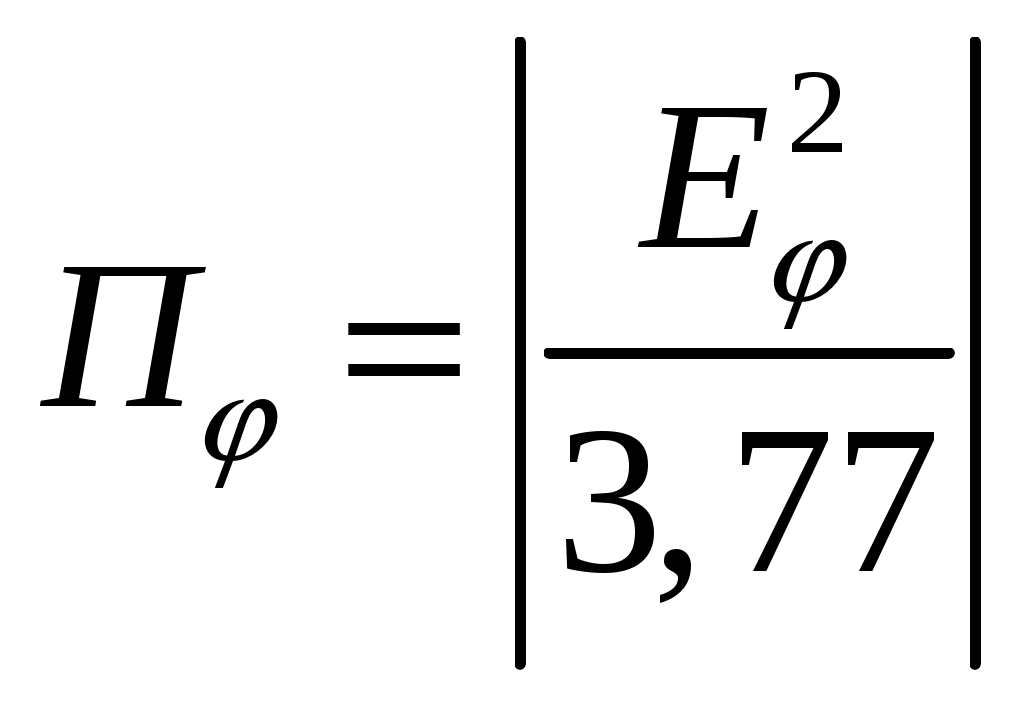, мкВт/см² (2.38)

10. Если требуется найти декартовые составляющее дифракционного поля, то следует воспользоваться следующими формулами:

;

;

(2.39)

В секторе углов, принадлежащих подобласти II-б, значения сферических компонент дифракционного поля определяются одной "светящейся" точкой (точка А на рис.2.5) по формулам:

, (2.40)

(2.41)

В этих формулах: E₀ определяется в соответствии с (2.36),  = 0,316, коэффициенты дифракции рассчитываются по формулам (2.28)...(2.32).

Переход к декартовым составляющим дифракционного поля осуществляется по формулам (2.39), а к сферическим компонентам ППЭ по формулам (2.38).

В секторе углов подобласти II-в следует принять, что П_диф = 0.

Расчет плотности потока энергии в области III. Если зеркало антенны длиннофокусное ( < 90°), то в области III ППЭ имеет две составляющие. Одна определяется излучением облучателя, другая - дифракцией на части кромки:

(2.42)

Составляющая П_обл определяется по формуле (2.23) с последующим переходом к мкВт/см², а составляющая П_диф так же, как для подобласти II-б.

В случае короткофокусной антенны ( < 90°) в области III ППЭ имеет составляющие П_диф и П_а. Составляющая П_диф рассчитывается так же, как для подобласти II-а - по формулам (2.28)... (2.38).

Расчет плотности потока энергии в области IV. В области IV ППЭ определяется в основном составляющими П_обл и П_диф, поэтому значение ППЭ в этой области формально определяется по формуле (2.42) с добавлением составляющей П_а. При этом дифракционная составляющая поля определяется так же, как это сделано в подобласти II-а - по формулам (2.28)... (2.38).

Расчет плотности потока энергии в области V. В этой области ППЭ следует определять следующим образом:



При этом составляющая П_а рассчитывается по формулам (2.25) и (2.26), после того как предварительно геометрически определена граница раздела между областями IV и V (значение) на выбранном азимутальном направлении.

Алгоритм определения областей и подобластей для расчетной точки и примеры расчета ППЭ приведены в приложении 2 - рис.П1.3 и П1.4.

Примеры расчета ППЭ вблизи параболических антенн с круглой апертурой приведены в приложении 2.
3. Расчет плотности потока энергии вблизи параболических антенн с квадратной и прямоугольной апертурой
Квадратная апертура. При анализе квадратной апертуры (рис.3.1) используются допущения:

- распределение амплитуды поля в одной из главных плоскостей - "косинус на пьедестале":

, где (3.1)

a - сторона квадрата,  - текущее значение координаты апертуры в одной из главных плоскостей;

- облучатель и антенна имеют характеристики направленности с осевой симметрией относительно направлений их максимального излучения;

- значение характеристики направленности облучателя вне сектора углов перехвата энергии основным зеркалом равно 0,316 (по напряженности поля).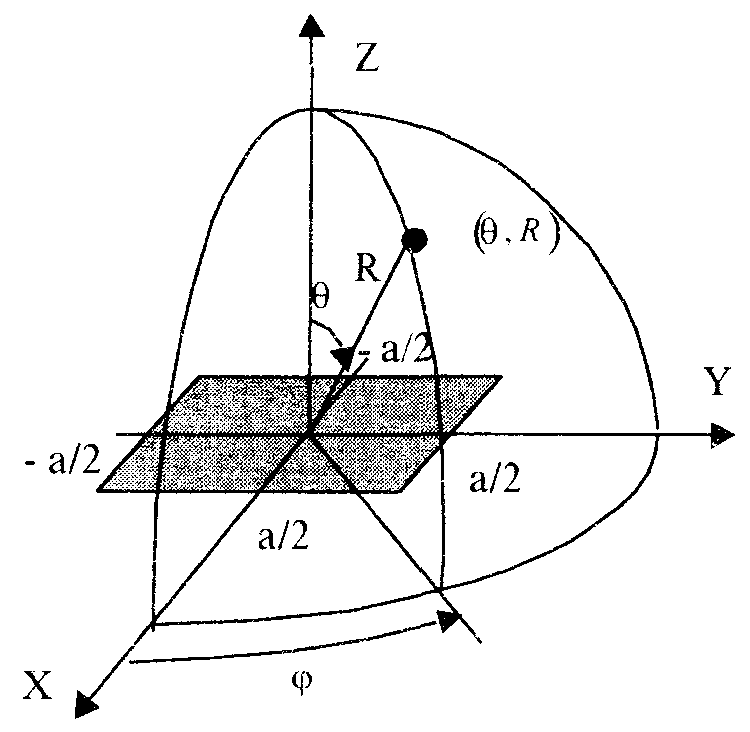


Рис.3.1. Квадратная апертура.
Общая расчетная формула для определения значения ППЭ имеет вид (2.1). Физический смысл отдельных составляющих прежний. Составляющие П_а и П_обл в децибелах относительно 1 мкВт/см² будут иметь вид:

, дБ, (3.2)

, дБ, где (3.3)

P - мощность, излучаемая антенной, Вт;

- длина волны, м;

a - сторона квадрата (апертуры антенны), м;

D₀ - КНД антенны в направлении максимального излучения в волновой зоне;

B(x) - функция, учитывающая изменение КНД квадратной апертуры в зависимости от относительного расстояния;

F(u, x) - нормированная ХН квадратной апертуры в координатах u, x;

, R - сферические координаты расчетной точки;

u = ( a sin )/ - обобщенная координата угла;

x = R/R_гр - относительное расстояние;

R_гр = 2a² /  - граничное расстояние.

D_обл - КНД облучателя в направлении максимального излучения (величина безразмерная). График зависимости D_обл, Дб = 10lg D_обл как функции аргумента ₀ для усредненной модели антенн приведен на рис.П1.2 (приложение 1).

Вычисление функции F(u, x) сводится к расчету характеристики направленности линейного синфазного источника (рис.3.2) с распределением амплитуды тока, совпадающим с распределением амплитуды поля вида (3.1).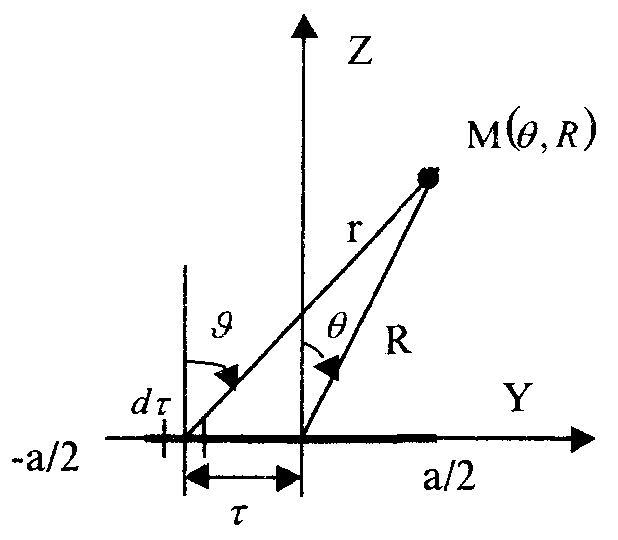


Рис.3.2. К расчету характеристики направленности.
Значение напряженности поля в расчетной точке определяется выражением: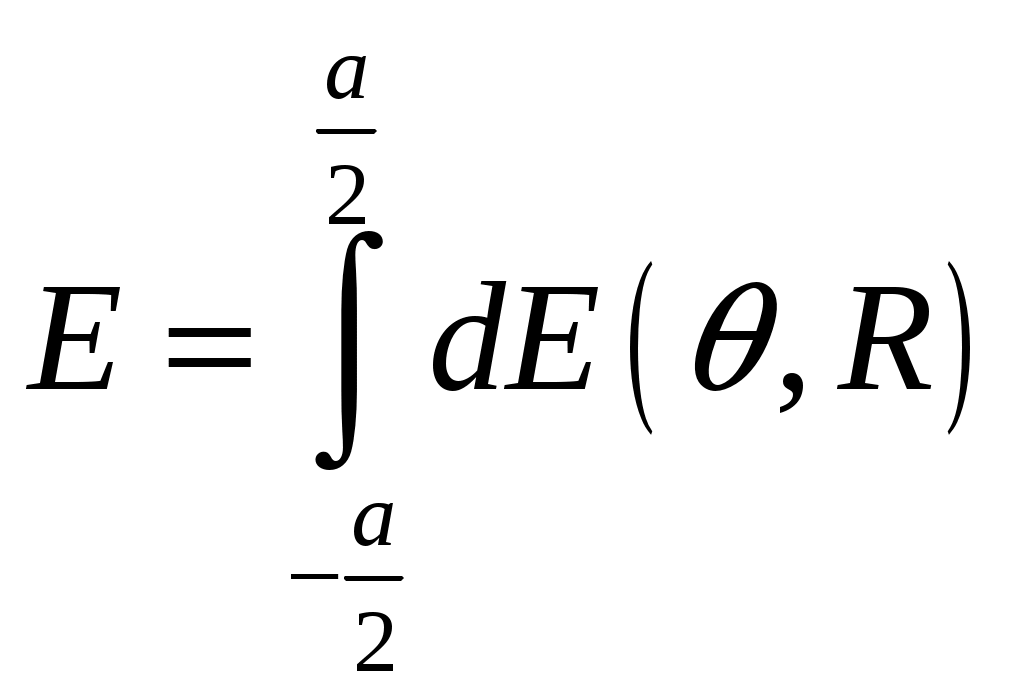

, где (3.4)

(3.5)

В (3.5) f() определяется распределением поля, а геометрические параметры , r являются функциями , R.

Нормированная характеристика направленности апертуры имеет вид: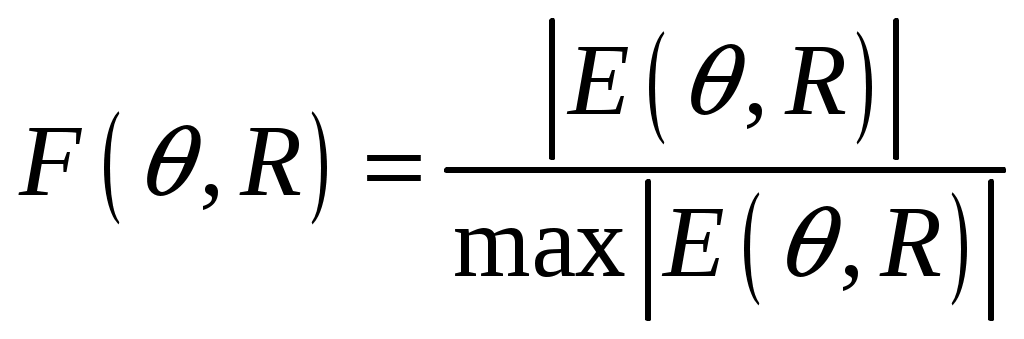

(3.6)

В терминах обобщенных координат (u, x) направленные свойства апертуры будут характеризоваться функцией F(u, x).

Функции F(u, x) сильно осциллирующие, поэтому в практических расчетах ППЭ следует использовать их гарантированные огибающие. Для удобства практических расчетов гарантированные огибающие табулированы (приложение 3, таблицы 3.1 и 3.2). При значениях x> 1, что соответствует дальней зоне, необходимо пользоваться огибающими для x = 1.

Аналитическое выражение функции B(x)/x для квадратной апертуры с амплитудным распределением типа "косинуса на пьедестале" имеет вид: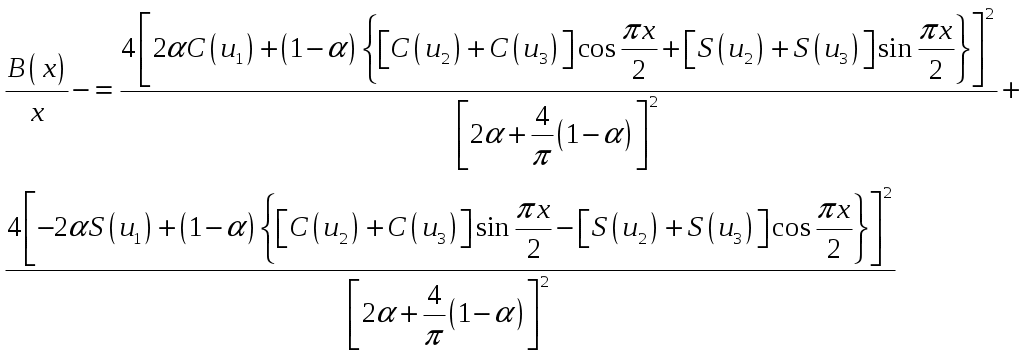

(3.7)

где , , ; (3.8)

- косинус интеграла Френеля; (3.9)

- синус интеграла Френеля (3.10)

В области x  1 функция (3.7) осциллирующая, а в области x > 0,15 - изменяется монотонно. При расчете ППЭ осциллирующую часть функции следует заменить огибающей ее максимумов.

На рис.П3.1 (приложение 1) приведена функция 20 lg(B(x)/x). В области x > 1 функция 20lg(B(x)/x) = -20 lgx.

Порядок расчета ППЭ в переднем полупространстве не отличается от приведенного для круглой апертуры.

Для расчета ППЭ в области заднего полупространства вводится понятие эквивалентной круглой апертуры. Диаметр эквивалентной апертуры определяется из условия равенства площадей квадратной и круглой апертур:

(3.11)

Угол раскрыва эквивалентной апертуры определяется по формуле:

, где (3.12)

f - фокусное расстояние зеркала.

Прямоугольная апертура. Прямоугольная апертура со сторонами a и b показана на рис.3.3.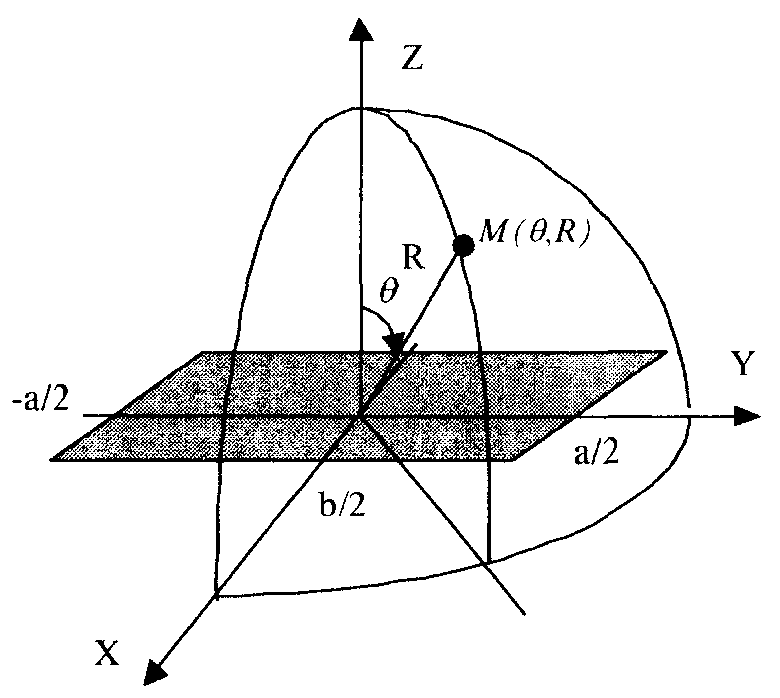


Рис.3.3. Прямоугольная апертура.
Расчетная формула для апертурной составляющей ППЭ имеет вид: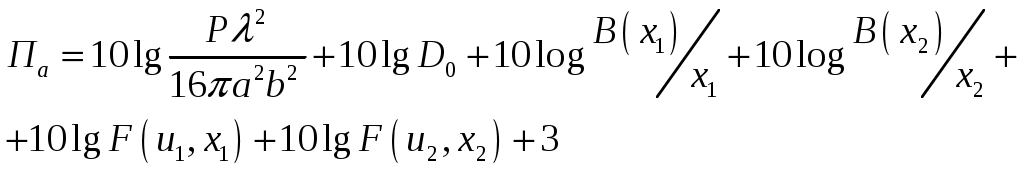

, где (3.13)

, , , (3.14)

Функции F(u, x), входящие в (3.13), вычисляются в соответствии с (3.4)...(3.6) с учетом перехода к обобщенным координатам u и x, а функции B(x)/x - по формуле (3.7) при x = x₁ и x = x₂, соответственно.

Расчет составляющей ППЭ от облучателя выполняется по формуле (3.3). КНД облучателя следует рассчитывать по формуле:

, где (3.15)

D₁ и D₂ определяются по формулам (2.15) и 2.16) с учетом различных значений угла ₀ в главных плоскостях.

Диаметр эквивалентной круглой апертуры, необходимый для расчета дифракционной составляющей ППЭ, определяется из условия равенства площадей прямоугольной и круглой апертур:

(3.16)

Угол раскрыва эквивалентной круглой апертуры определяется по формуле (3.12).

Примеры расчета ППЭ вблизи параболических антенн с квадратной и прямоугольной апертурами приведены в приложении 3.
4. Расчет плотности потока энергии вблизи антенн типа параболический цилиндр и рупорных антенн
Антенна типа параболический цилиндр. Антенна имеет прямоугольную апертуру (рис.4.1). Распределение амплитуды поля вдоль сторон апертуры в главных плоскостях XOZ и ZOY равномерное. Методика расчета ППЭ соответствует случаю прямоугольной апертуры f() = const. Огибающие F(u, x) для случая f() = const отличаются от аналогичных кривых, соответствующих распределению (3.1), не существенно (единицы дБ). Поэтому в практических расчетах можно использовать данные, приведенные в табл.П3.1 и табл.П3.2.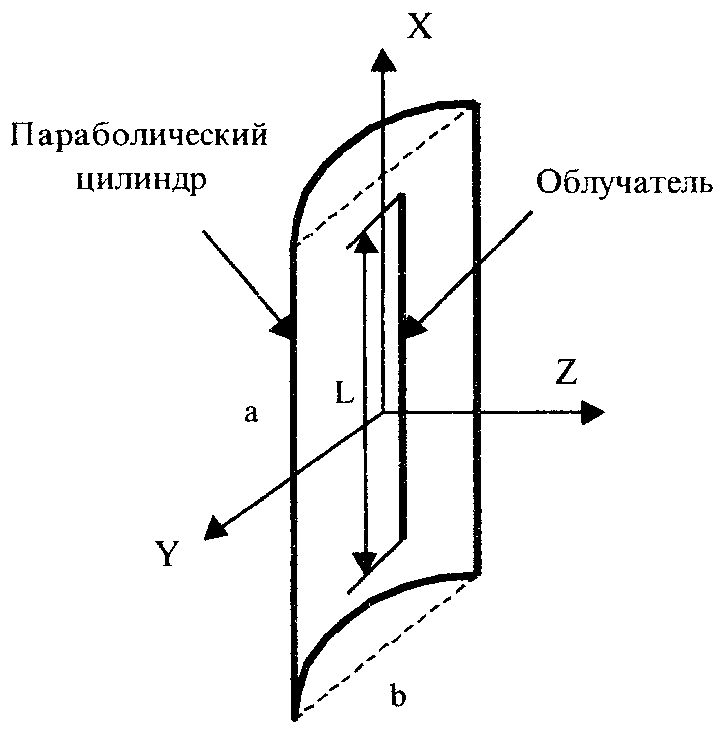


Рис.4.1. Антенна типа параболический цилиндр.
Значение КНД облучателя рассчитывается по формуле: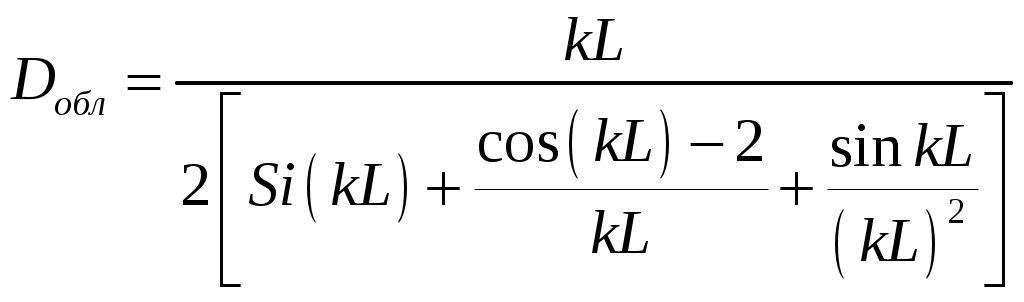

, где (4.1)

L - длина облучателя;

;

- интегральный синус.

В области заднего полупространства расчет ППЭ следует вести по формуле (3.3), приняв D_обл= D₀.