Методы контроля. Методические указания мук 116702 ббк 51. 21
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
Пирамидальный рупор. Пирамидальные (рис.4.2) и конические (рис.4.3) рупорные антенны имеют апертуры с неравномерным и несинфазным возбуждением. Линейные размеры апертур обычно измеряются единицами, реже десятками длин волн. Расчетные точки, находящиеся на расстоянии нескольких метров от таких антенн, относятся к дальней (волновой) зоне. 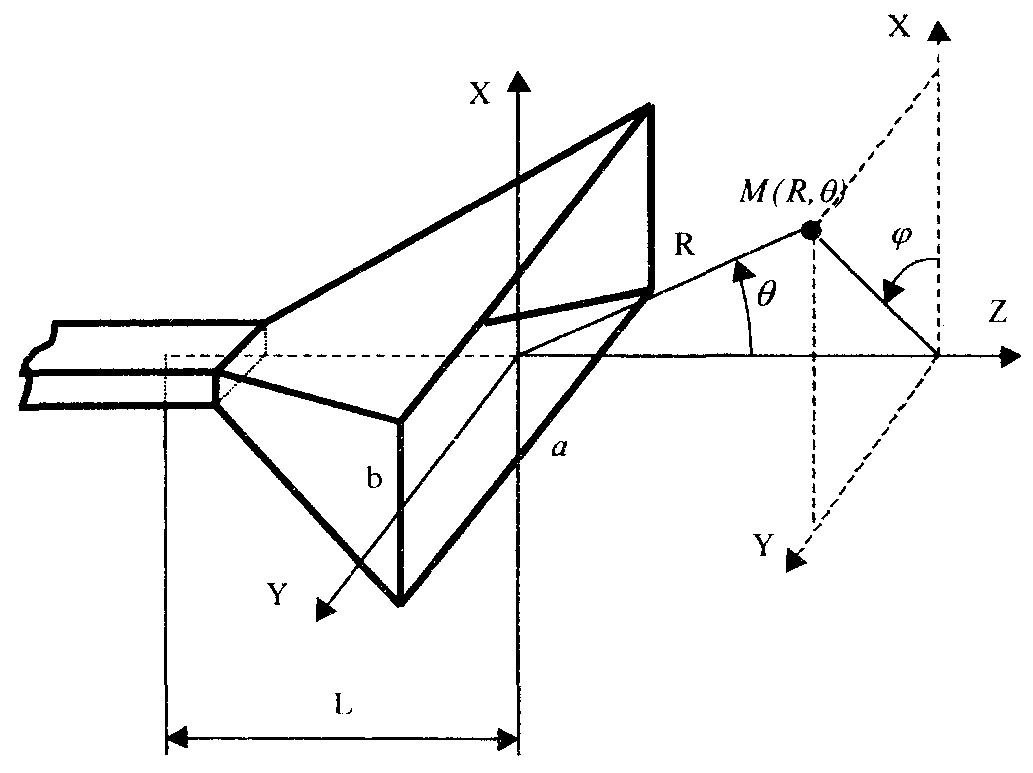 Рис.4.2. К расчету ППЭ вблизи пирамидального рупора. 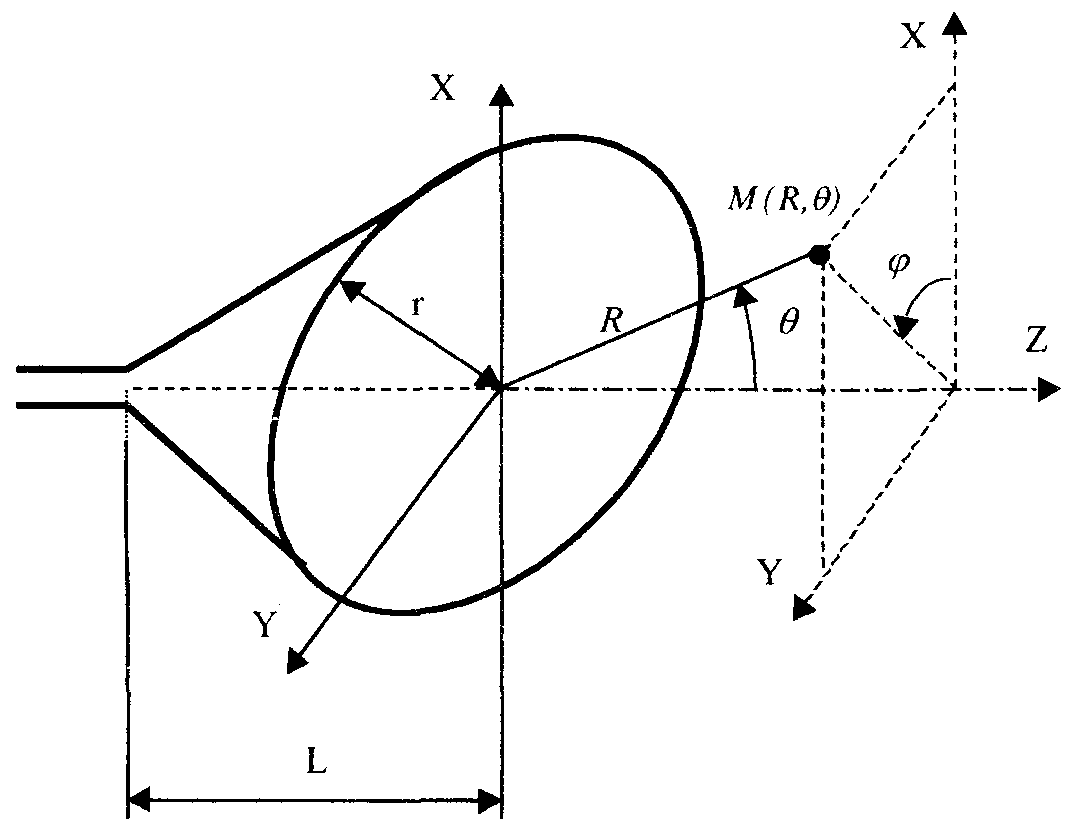 Рис.4.3. К расчету ППЭ вблизи конического рупора. Плотность потока энергии в переднем полупространстве вблизи таких антенн рассчитывается по формуле: P - мощность, излучаемая антенной, Вт; F(, ) - характеристика направленности рупора; Dp - КНД рупора. Для пирамидального рупора в расчетах следует принять: сомножители - это нормированные характеристики направленности рупорной антенны в E и H плоскостях. Для расчета характеристики направленности в плоскости E ( = 0) сначала вычисляется функция: 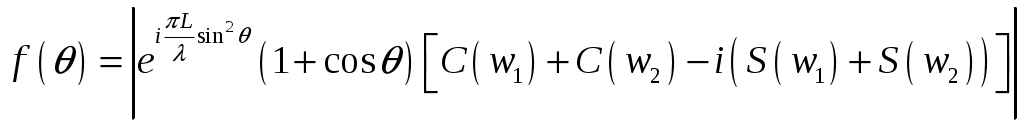 , где (4.4) , где (4.4)L, b - геометрические параметры рупора в E плоскости; C(w1), C(w2) - косинусы интеграла Френеля 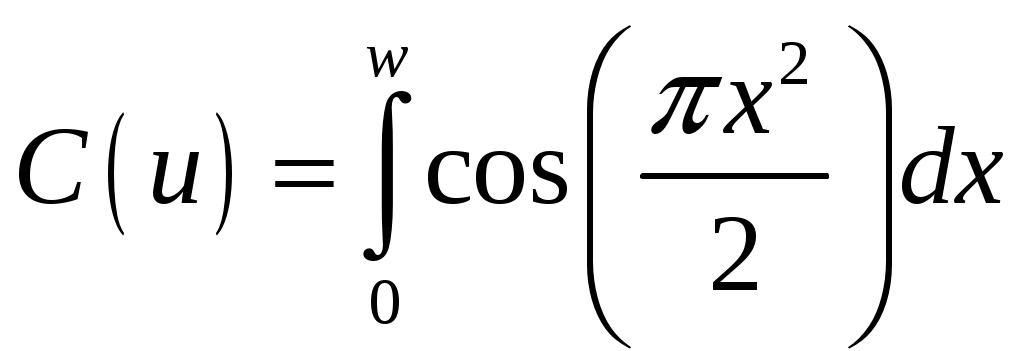 ; ;S(w1), S(w2) - синусы интеграла Френеля 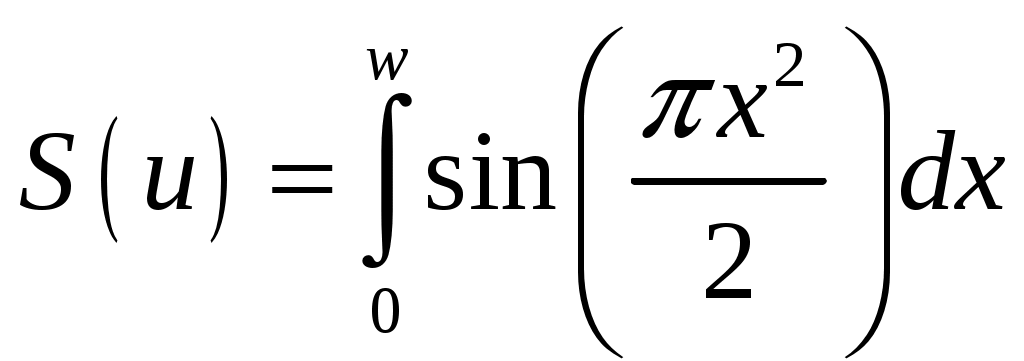 . .Нормированная характеристика направленности имеет вид: Для расчета характеристики направленности в плоскости 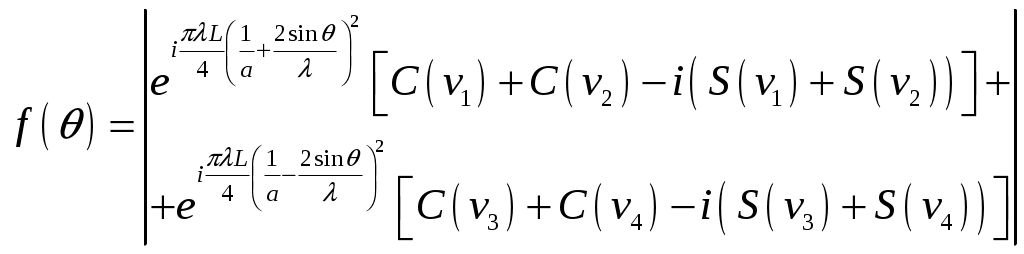 , где (4.7) , где (4.7)L, a - геометрические параметры рупора в H плоскости; C(v1), C(v2), C(v3), C(v4) - косинусы интеграла Френеля; S(v1), S(v2), S(v3), S(v4) - синусы интеграла Френеля. Нормированная характеристика направленности имеет вид: Значение КНД пирамидальной рупорной антенны рассчитывается по формуле: 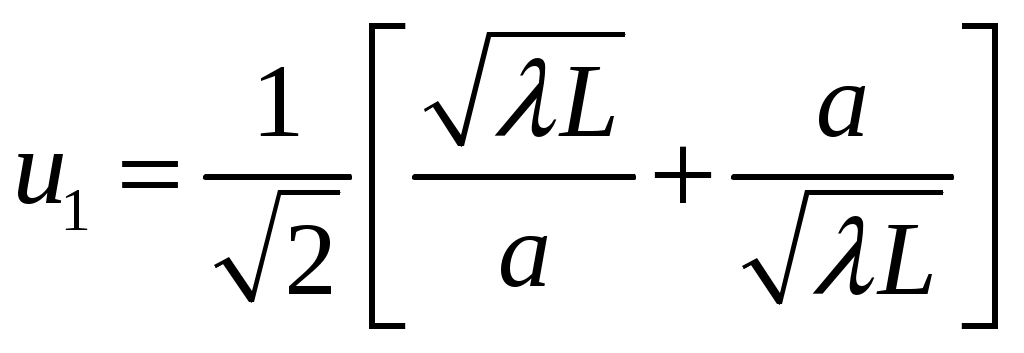 , , 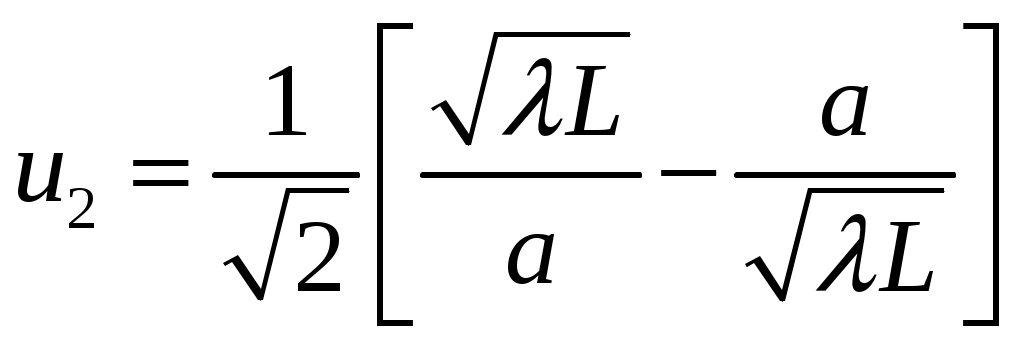 , , C(u1), C(u2), C(u3) - косинусы интеграла Френеля; S(u1), S(u2), S(u3) - синусы интеграла Френеля. Конический рупор. Для конического рупора функция F(, ) рассчитывается следующим образом. Сначала для заданного угла вычисляется ненормированная характеристика направленности: 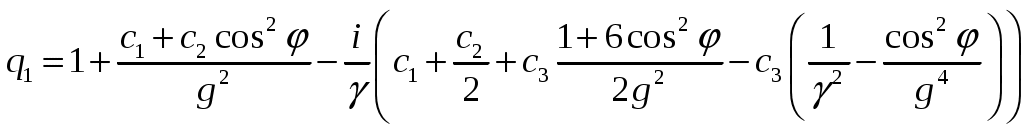 ; (4.13) ; (4.13)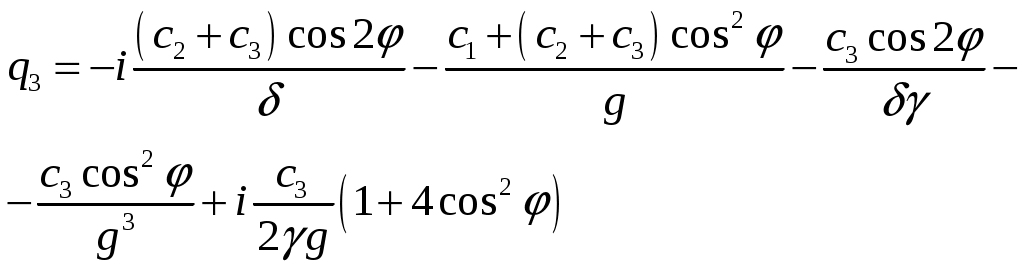 ; (4.15) ; (4.15)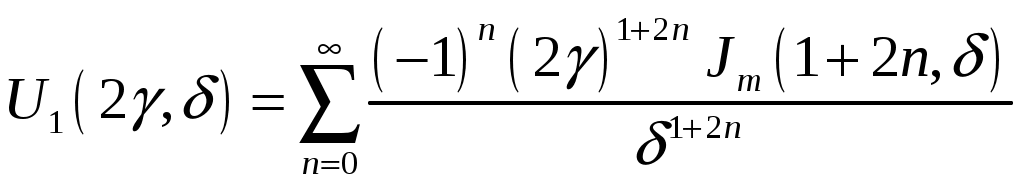 - функция Ломмеля 1-го порядка; (4.17) - функция Ломмеля 1-го порядка; (4.17)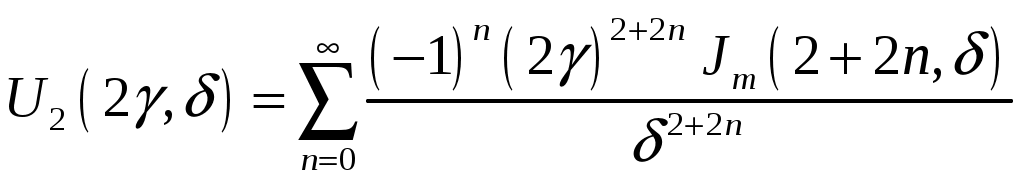 - функция Ломмеля 2-го порядка; (4.18) - функция Ломмеля 2-го порядка; (4.18)c1 = -0,37, c2 = -0,845, c3 = 0,215 - коэффициенты, соответствующие волне возбуждения H11 (при равномерном возбуждении апертуры c1 = c2 = c3 = 0); J0 (), J1()- функции Бесселя соответственно нулевого и первого порядка. Сходимость рядов обеспечивается при n = 40. Нормированная характеристика направленности имеет вид: Значение КНД конической рупорной антенны рассчитывается по формуле: В области заднего полупространства расчет ППЭ выполняется по формуле: Примеры расчетов ППЭ вблизи антенн типа параболический цилиндр, пирамидального и конического рупора приведены в приложении 4. 5. Расчет плотности потока энергии вблизи рупорно-параболической и перископической антенн Конструкция типовой рупорно-параболической антенны (РПА) схематично представлена на рис.5.1. Апертуру можно считать квадратной с размером 2,7х2,7 м2. Методика расчета ППЭ в переднем полупространстве (Y > 0) соответствует приведенной в разделе 3 для квадратной апертуры с распределением амплитуды поля (3.1) - "косинус на пьедестале". Составляющая Па рассчитывается по формуле (3.2), составляющая Побл - по формуле (3.3). При этом угол раскрыва рупора 20 = 235°. Учитывая, что РПА обладает хорошим защитным действием (уровень бокового излучения исключительно низок: почти во всем секторе углов он не превосходит -60... -70 дБ), дифракционную составляющую и составляющую Побл при расчете ППЭ в области заднего полупространства (Y < 0) не учитывать. 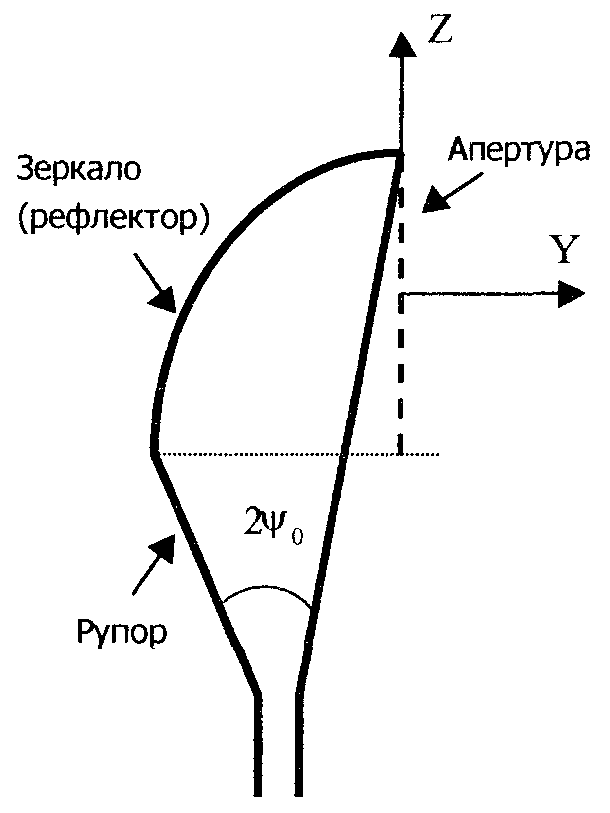 Рис.5.1. Рупорно-параболическая антенна. Перископические антенные системы (ПАС) обычно строятся по трехэлементной схеме (рис.5.2) - первичный рупорный облучатель, нижнее зеркало и верхнее зеркало. Диаметр верхнего зеркала 3,9 м, нижнего 3,2 м. Диаметры апертур с учетом наклонного положения зеркал следует брать равными 0,7 реальных диаметров зеркал. 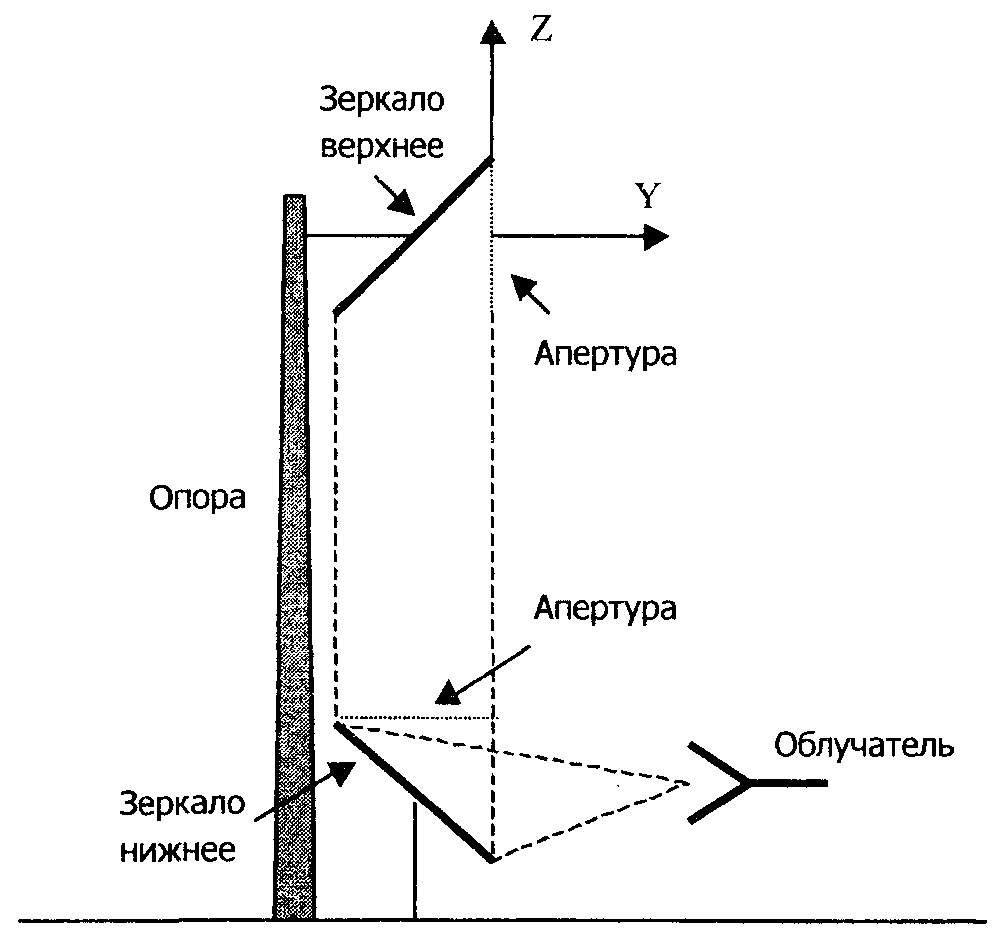 Рис.5.2. Перископическая антенная система. В общем случае значение ППЭ в произвольной точке пространства M определяется тремя составляющими, каждая из которых соответствует одной из трех антенн - А1, А2, А3 (рис.5.3). 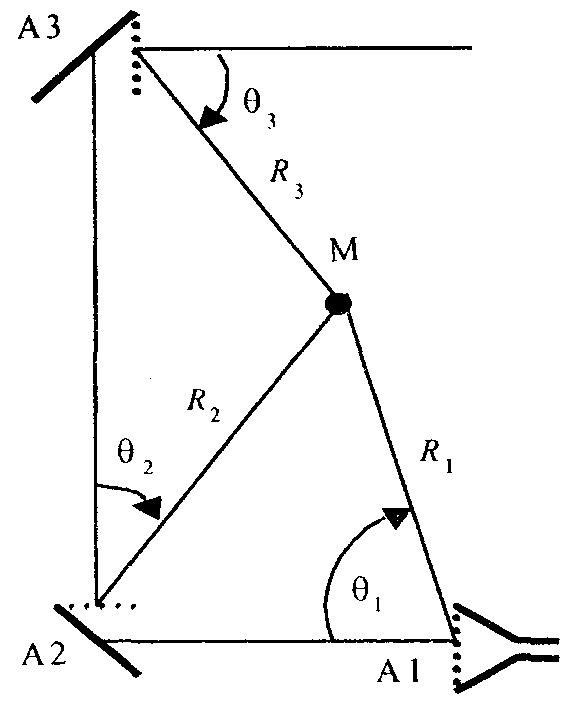 Рис.5.3 К расчету ППЭ вблизи ПАС. Антенна А1 рупорная. Ее вклад в значение ППЭ определяется в соответствии с методикой, изложенной в разделе 4. Антенны А2 и А3 имеют круглые апертуры. Их вклад в значение ППЭ определяется апертурными составляющими, которые рассчитываются по формуле (2.8). Вблизи поверхности земли значение ППЭ определяется в основном антенной А1 - облучателем, поэтому вклад апертурных составляющих верхнего и нижнего зеркала можно не учитывать. В области Y < 0 следует ограничиться только составляющей от антенны А1, то есть не учитывать составляющие ППЭ, обусловленные дифракцией электромагнитных волн на зеркалах. Примеры расчета ППЭ вблизи антенн РПА и ПАС приведены в приложении 5. 6. Учет влияния решетчатой структуры рефлектора Решетчатая структура рефлектора создает повышенный (по сравнению с зеркалом из сплошного листа) уровень ППЭ в области заднего полупространства антенны. При облучении рефлектора электромагнитной энергией происходит ее отражение (полезный эффект, связанный с формированием диаграммы направленности антенны) и частичное прохождение в область заднего полупространства (рис.6.1). 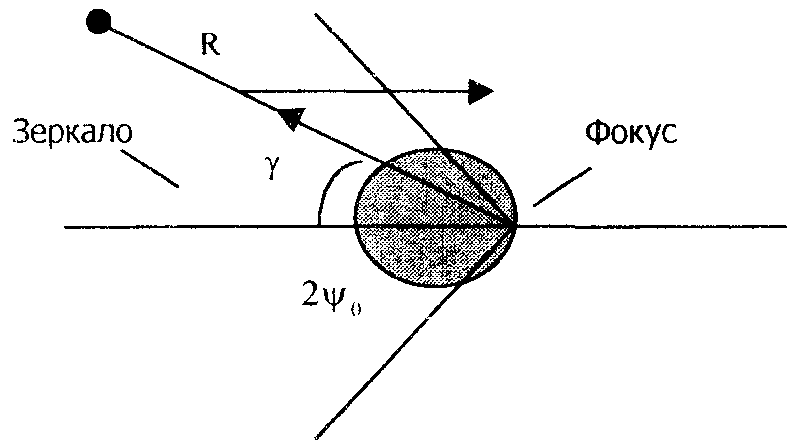 Рис.6.1. Прохождение энергии через зеркало. Значение составляющей Ппр в точке М, находящейся в области заднего полупространства, определяется по формуле: Т - коэффициент прохождения волны через решетчатую структуру (по полю); Р - мощность излучения облучателя, Вт; Dобл - коэффициент направленного действия облучателя (величина безразмерная); Fобл() - характеристика направленности облучателя (величина безразмерная); R - расстояние от фазового центра облучателя до расчетной точки M, м. Угловая зависимость коэффициента прохождения не учитывается. Значение T определяется для случая нормального падения плоской волны на безграничную плоскую решетчатую структуру. Характеристика направленности облучателя в области углов 0 < 0 имеет вид: 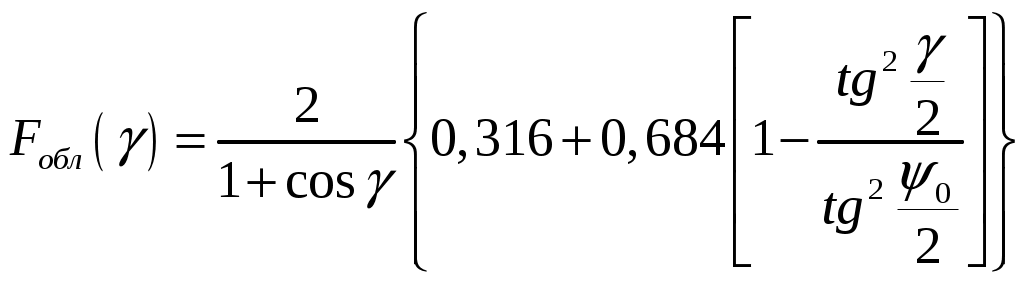 (6.2) (6.2)Значение КНД облучателя рассчитывается по формуле (2.15). Для случая выполнения рефлектора (зеркала) из сетки линейных проводников (рис.6.2) формула для расчета коэффициента прохождения по полю имеет вид: 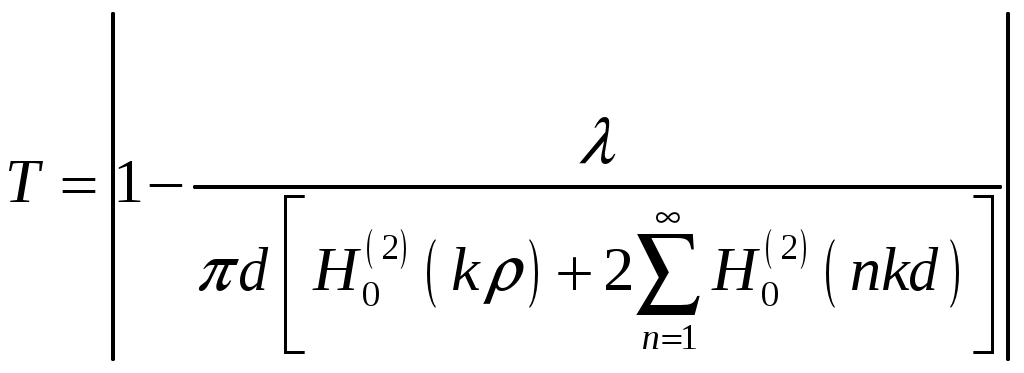 , где (6.3) , где (6.3)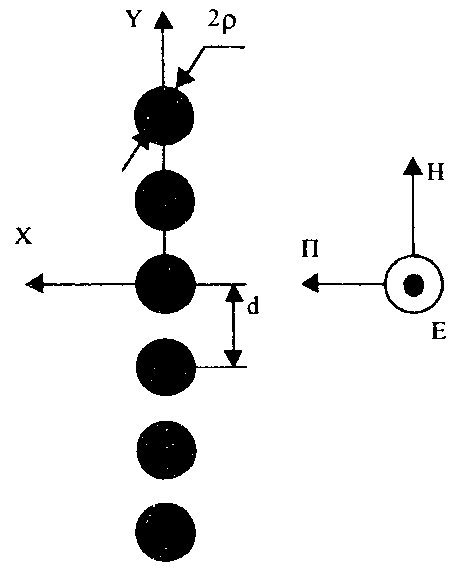 Рис.6.2. Падение плоской волны на проволочную сетку. Функции Бесселя рассчитываются по формулам: 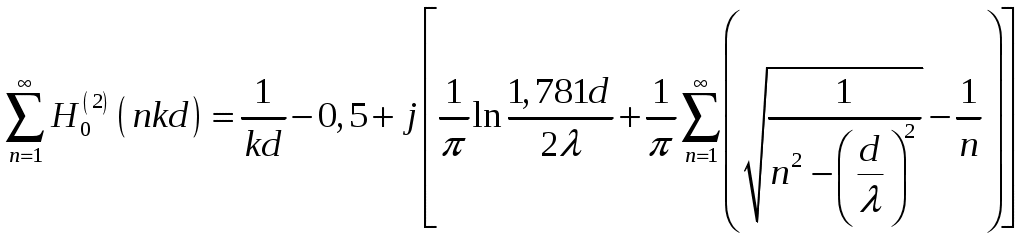 (6.5) (6.5)Ряд, стоящий в правой части (6.5), сходится достаточно быстро (можно ограничиться десятью членами). В случае выполнения отражательного зеркала в виде поверхности со щелями (рис.6.3а) при длине щелей, отвечающих условию (t > ), считать, что полоски и щели имеют безграничную длину (рис.6.3б).
Рис.6.3. К расчету коэффициента прохождения через поверхность со щелями. Для практически важного случая d < (0,4…0,5), формула расчета коэффициента прохождения имеет вид: 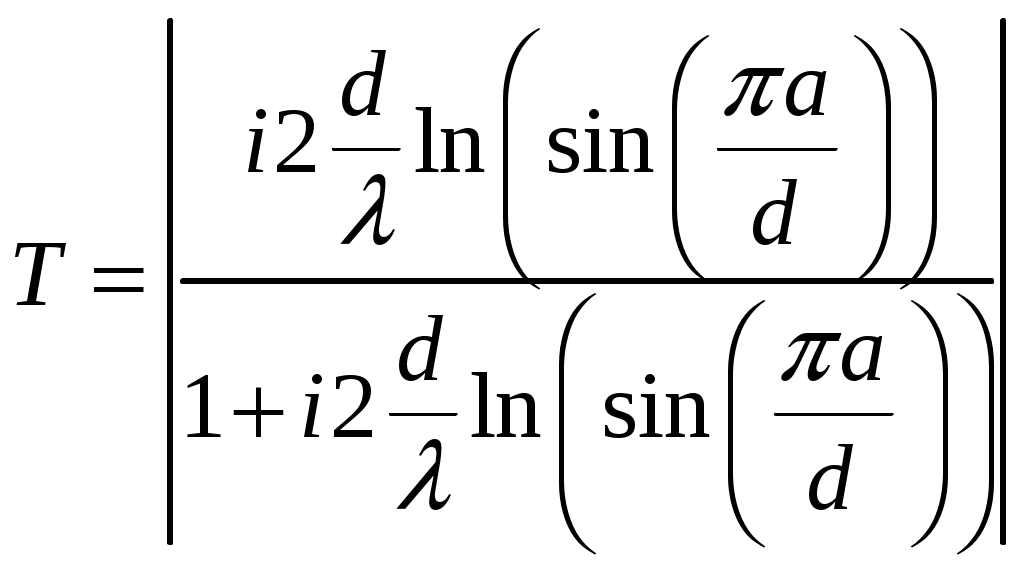 (6.6) (6.6)Для поверхности с круглыми отверстиями (рис.6.4) и расстоянии между центрами отверстий d < (0,3…0,4) формула для расчета коэффициента прохождения имеет вид: d - расстояние между щелями, D - диаметр щели, t - толщина отражающей поверхности. 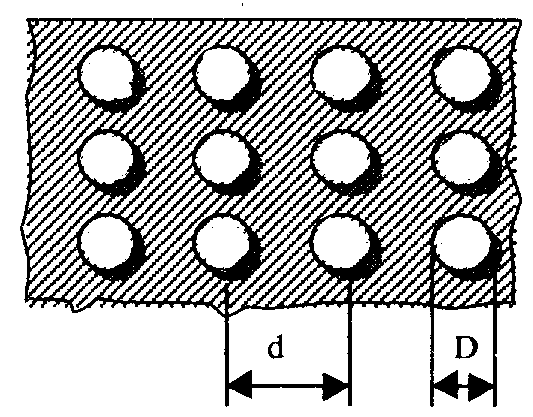 Рис.6.4. К расчету коэффициента прохождения через поверхность с отверстиями. В тех случаях, когда геометрические параметры решетчатой структуры не позволяют рассчитать коэффициент прохождения или структура решетки существенно отличается от рассмотренных, следует брать T = 0,01...0,02. Пример расчета ППЭ с учетом решетчатой структуры рефлектора приведен в приложении 6. 7. Расчет плотности потока энергии вблизи вибраторных антенн Расчет ППЭ вблизи вибраторных антенн осуществляется по формуле: Вычислению векторов напряженности электрического и магнитного полей предшествует решение электродинамической задачи о нахождении функции распределения тока (токовой функции) в проводниках антенны при заданном возбуждении. Данная задача решается в приближении тонкого провода с использованием интегрального уравнения Харрингтона. При этом используется метод коллокации (метод сшивания в точках) при кусочно-синусоидальном базисе разложения токовой функции. Антенна представляется системой цилиндрических проводников, радиус которых не превышает 0,02. Проводники разбиваются определенным образом на короткие отрезки (сегменты), длина которых не превышает 0,1. Соседние сегменты (на одном проводнике) частично перекрываются: начало некоторого данного сегмента совпадает с центром предыдущего, конец - с центром последующего. Интегральное уравнение Харрингтона имеет вид: 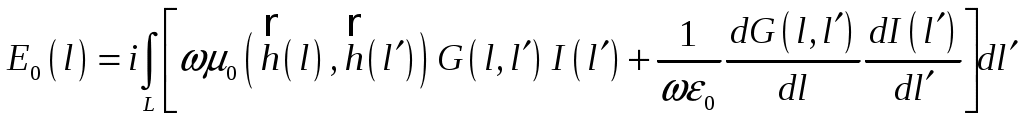 , где (7.2) , где (7.2)E0(l) - стороннее поле; L - контур, последовательно проходящий по осям всех проводников - вдоль данного контура отсчитываются криволинейные координаты l и l’ (см. рис.7.1); - круговая частота; 0 - магнитная постоянная; 0 - диэлектрическая постоянная; 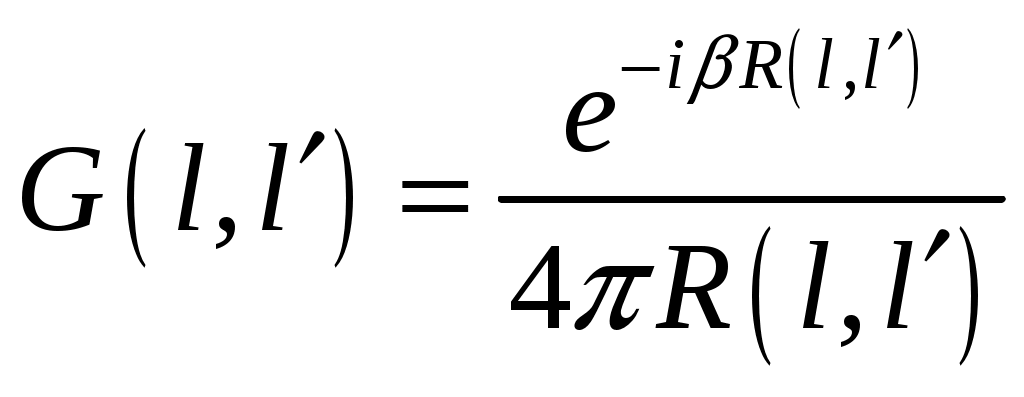 - функция Грина; - функция Грина;a(l) - радиус проводника в точке l; I(l’) - искомая токовая функция. 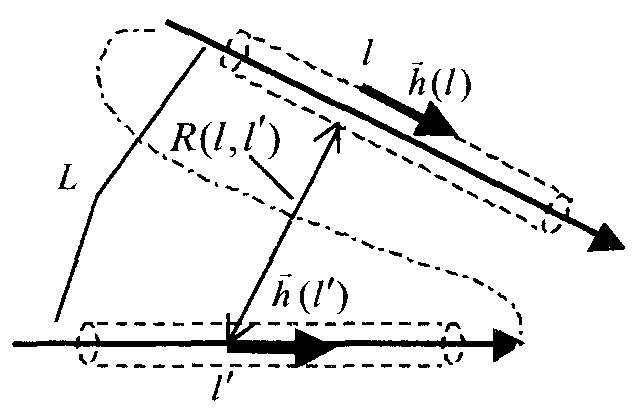 Рис.7.1. К решению интегрального уравнения. Искомая токовая функция I(l’) при выбранном базисе разложения определяется как линейная комбинация: M - число базисных функций, равное числу сегментов; Im - коэффициент при m-ой базисной функции; Bm (l’) - m-ая кусочно-синусоидальная базисная функция. Представление токовой функции в виде (7.3) сводит интегральное уравнение (7.2) к системе M линейных алгебраических уравнений относительно Im: k = 1, 2, ..., M N - число входов (активных вибраторов) антенны; Коэффициенты системы (7.4) рассчитываются по формуле: 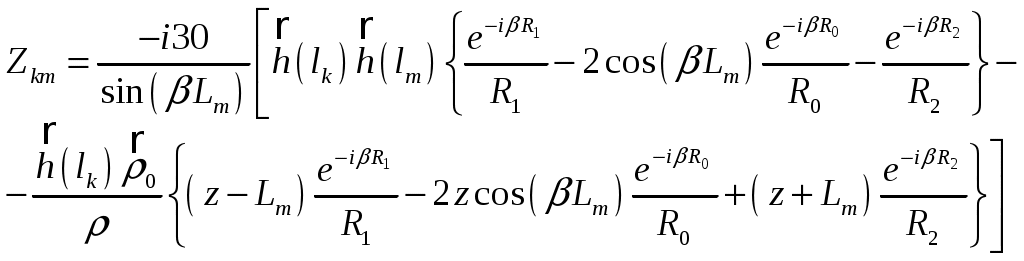 , где (7.5) , где (7.5)lk и lm - средние точки соответственно m-го и k-го сегментов; Lm - половина длины m-го сегмента; R1, R0 и R2 - расстояния до средней точки k-го сегмента соответственно от начальной, средней и конечной точек m-го сегмента; Первые M сегментов вводятся собственно на проводниках антенны. Сегменты с номерами, превышающими M, вводятся в областях зазоров активных вибраторов, к которым подводятся питающие напряжения (токи). Соответствующие им коэффициенты Zk,M+i, обусловливающие неоднородность системы (7.4), также рассчитываются по формуле (7.5). Найденные коэффициенты Im, будучи подставленными в (7.3), совместно с базисными функциями восстанавливают функцию, аппроксимирующую распределение тока по проводникам. Векторы напряженности электрического и магнитного полей в заданной точке наблюдения с радиус-вектором Векторы 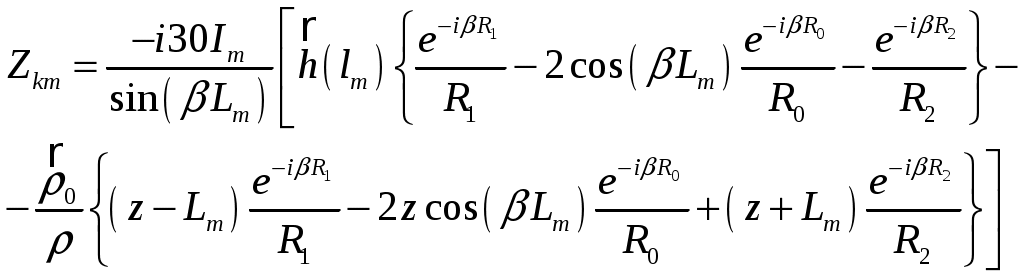 , (7.7) , (7.7)R1, R0 и R2 - расстояния между точкой наблюдения и соответственно начальной, средней и конечной точками m-го сегмента;  - -орт в цилиндрической системе, связанной с m-м сегментом. - -орт в цилиндрической системе, связанной с m-м сегментом.При m > M в формулах (7.7) и (7.8) в качестве коэффициентов Im берутся соответствующие заданные входные токи: Пример расчета ППЭ вблизи вибраторной антенны приведен в приложении 7. |