Методы контроля. Методические указания мук 116702 ббк 51. 21
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
2. Функция F(u, x) - круглая апертура u = 100...760 Таблица П 1.2
3. Функция 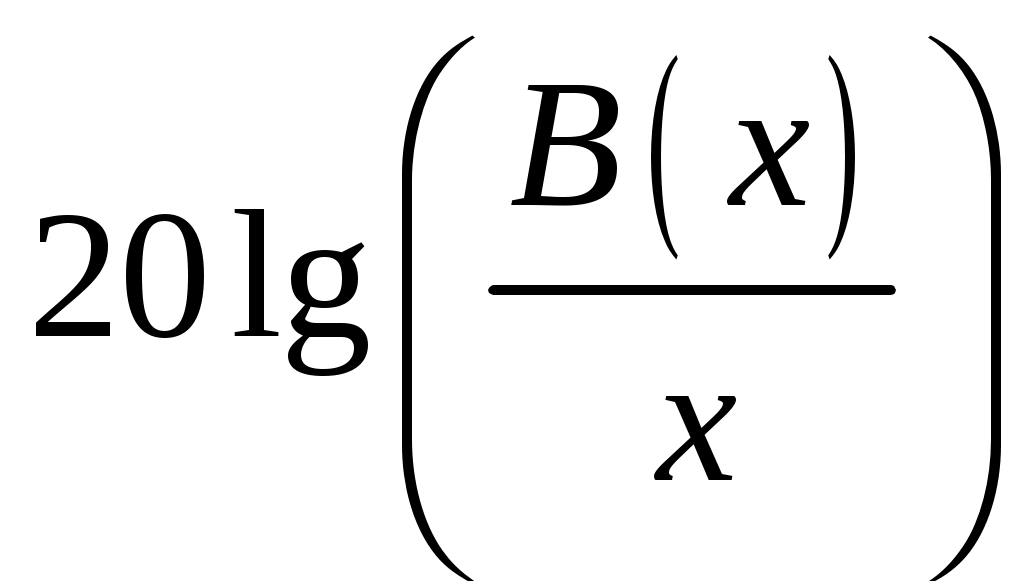 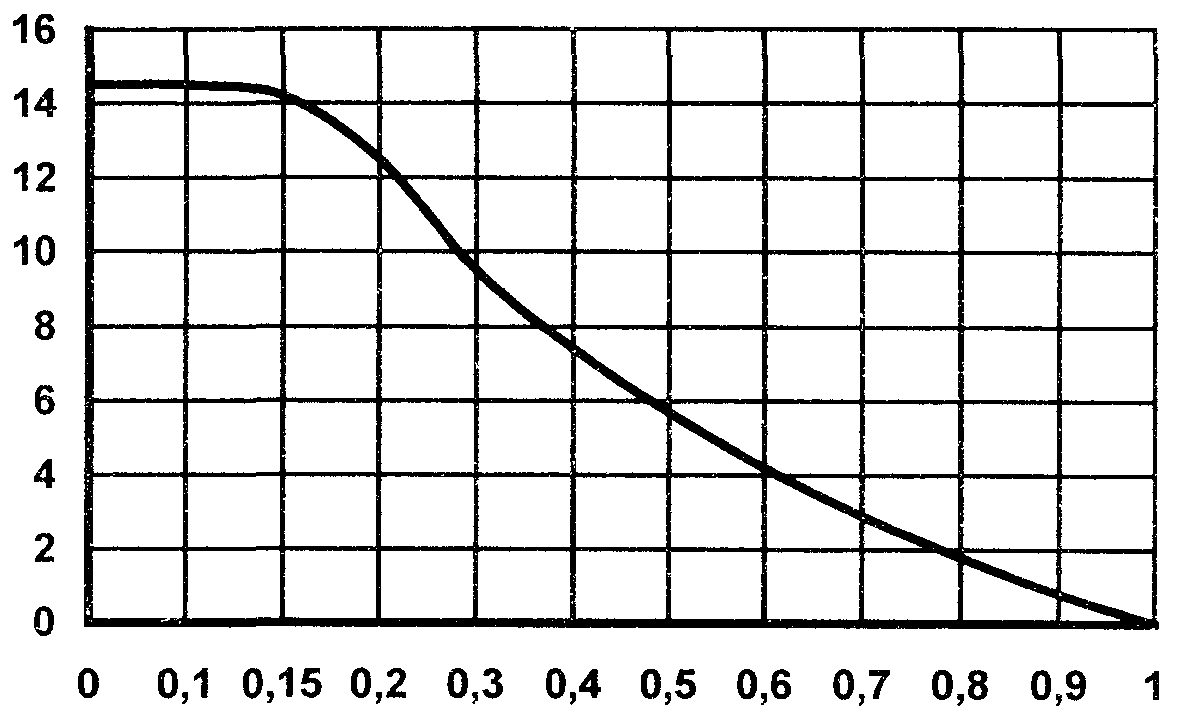 Рис.П1.1 4. Коэффициент направленного действия облучателя 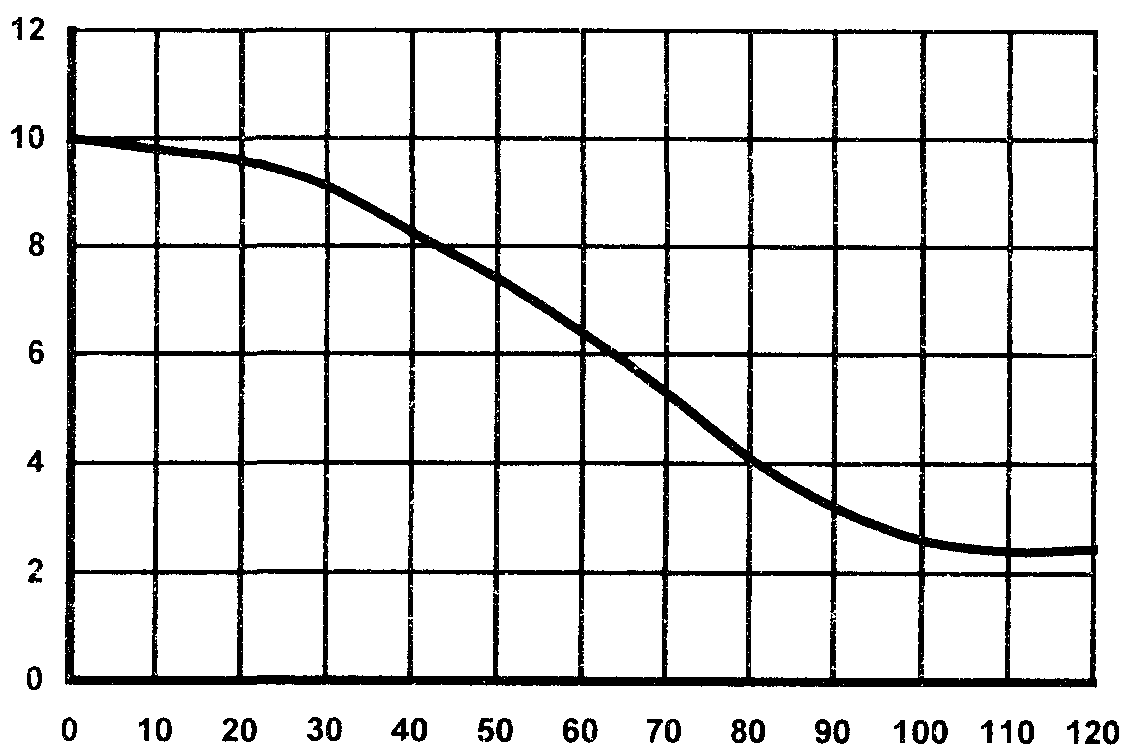 Рис.П1.2 5. Алгоритм определения положения расчетной точки 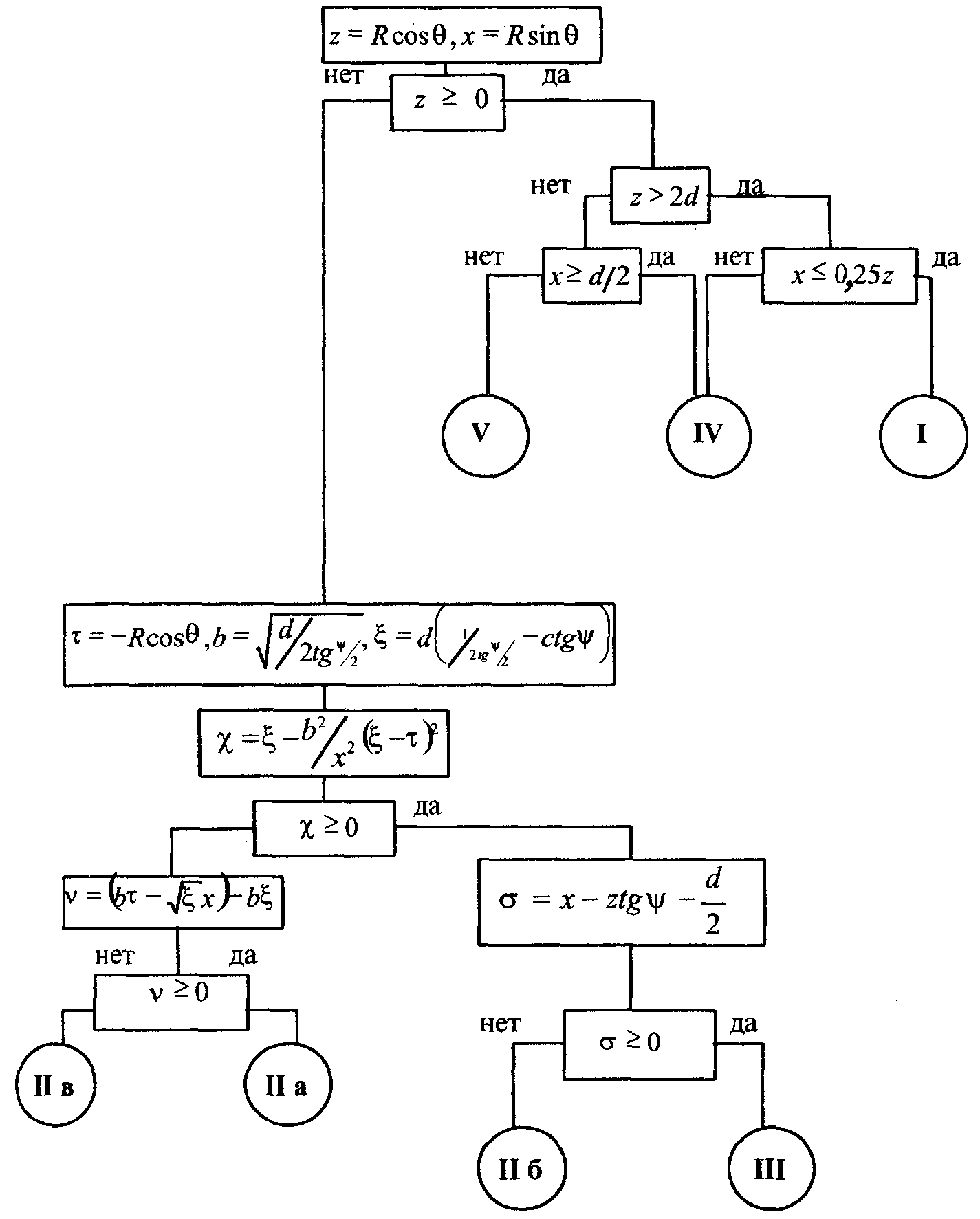 Рис.П1.3. Случай длиннофокусной антенны < /2. 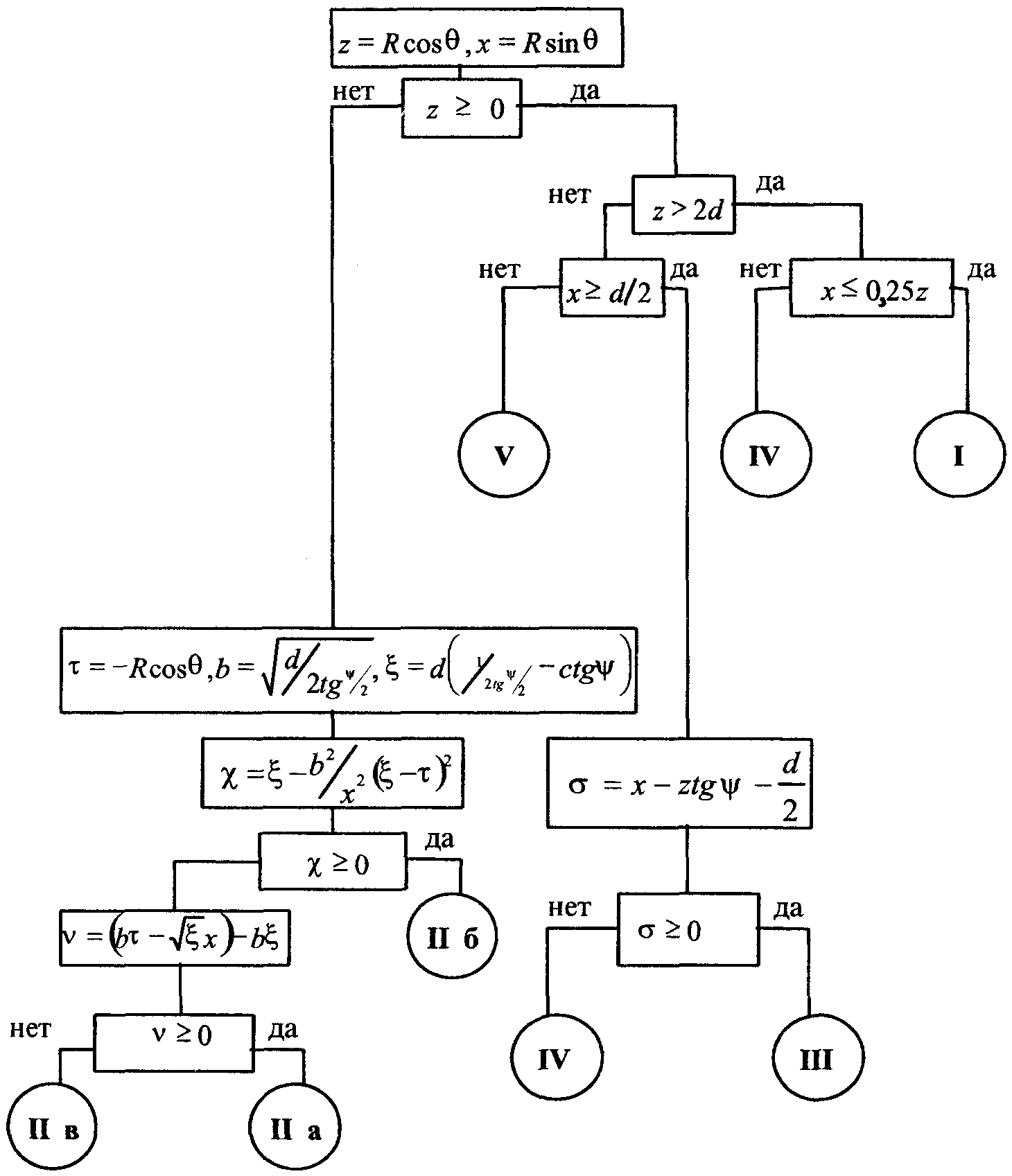 Рис.П1.4. Случай короткофокусной антенны < /2. Приложение 2 Примеры расчета ППЭ вблизи параболической антенны с круглой апертурой Пример 1 Исходные данные и постановка задачи Техническое средство - оборудование РРСП ПВ "Радуга-4" на оконечной радиорелейной станции. Работают три радиоствола. Мощность передатчика в каждом стволе 4 Вт. Используется антенна АДЭ-5 с диаметром антенны 5 м, углом раскрыва зеркала 20 = 210°, КНД 43,5 дБ. Антенна находится на высоте 50 м. Частота - 3658,54 МГц. Сравнить ППЭ в точках M1 и M2 с ПДУ ППЭ. Точка M1 расположена в направлении на соседнюю станцию, ее высота над поверхностью земли - 2 м, а удаление от основания мачты - 100 м. Точка M2 расположена в азимутальном направлении 180° на расстоянии 2 м от оси мачты на высоте 30 м. Постановка задачи иллюстрируется рис. П2.1.  Рис.П2.1. Иллюстрация к примеру расчета ППЭ. Решение Расчет ППЭ в точке M1 1. По алгоритму рис.П1.3 устанавливается принадлежность точки M1 к области IV. 2. Находится расстояние RM - "центр апертуры - точка M1" и угол M: При = 0 и = 0: 3. Находится граничное расстояние Rгр: Rгр = 2d2 / = 2 ··52 / 0,082 = 609,76 м 4. Определяются координаты x и u: x = RM / Rгр = 110,92 / 609,76 = 0,182, u = ( d sin M) / = ( · 5 · sin 25,63°) / 0,082 = 82,89 5. По таблице П1.1 определяется функция 20 lg F(u, x) = -52,16 дБ 6. По графику рис.П1.1 определяется функция 20 lg [B(x)/x] = 13,22 дБ 7. По формуле (2.8) рассчитывается = 10 lg (12 ··0,0822 / 54) + 43,5 + 13,22 - 52,16 + 3 = -31,33 дБ 8. По графику рис.П4.2 определяется значение Dобл. дБ = 10 lg Dобл = 2,396 дБ 9. По формуле (2.9) рассчитывается = 10 lg [12 / (4 · 110,922)] + 2,396 + 10 = -28,7 дБ 10. По формуле (2.24) рассчитывается суммарная ППЭ в точке M1 без учета дифракционной составляющей: 11. Дифракционная составляющая ППЭ рассчитывается по формулам (2.28)...(2.38), при этом: D1 = -0,0355 + i0,0323, D2 = 0,113 – i0,109, E = 0,0255 – i0,0266, 12. Рассчитывается суммарная ППЭ в точке M1 с учетом дифракционной составляющей: П = 2,084 · 10-3 + 3,602 · 10-4 = 2,44 · 10-3 мкВт/см2. Вывод: ППЭ в точке меньше ПДУ, равного 10 мкВт/см2. Расчет ППЭ в точке M2 1. Принимается, что = 95,7106° 2. По алгоритму рис.П1.4 устанавливается принадлежность точки M2 к области IIб. Учитывая, что зеркало антенны короткофокусное 20 > 180°, поле в точке M2 будет определяться только дифракционной составляющей. 3. По формуле (2.41) рассчитывается E = -7,256 · 10-2 + i1,273 · 10-2. При этом D2 = 0,114 – i0,107 (формулы (2.28)...(2.32)), E0 = 18,827 (формула (2.36)). 4. Определяется ППЭ в точке M2 по формуле (2.38): П = 1,44 · 10 мкВт/см2 Вывод: ППЭ в точке М2 меньше ПДУ, равного 10 мкВт/см2. Пример 2 Исходные данные и постановка задачи Техническое средство - ССП. Передатчик работает на длине волны = 0,05 м. Мощность передатчика Р = 3 кВт. Используется антенна Кассегрена с углом раскрыва 20 = 180° и D0 = 50 дБ. Диаметр апертуры d = 7 м. Высота центра апертуры над землей HA = 7 м. Направление максимального излучения составляет с плоскостью горизонта угол = 10°. Рассчитать ППЭ в точках M и N. Исходные данные: HM = 2 м, M = 5°, M = 300 м, HN = 4 м, N = 160°, N = 20 м. Постановка задачи иллюстрируется рис.П2.2. 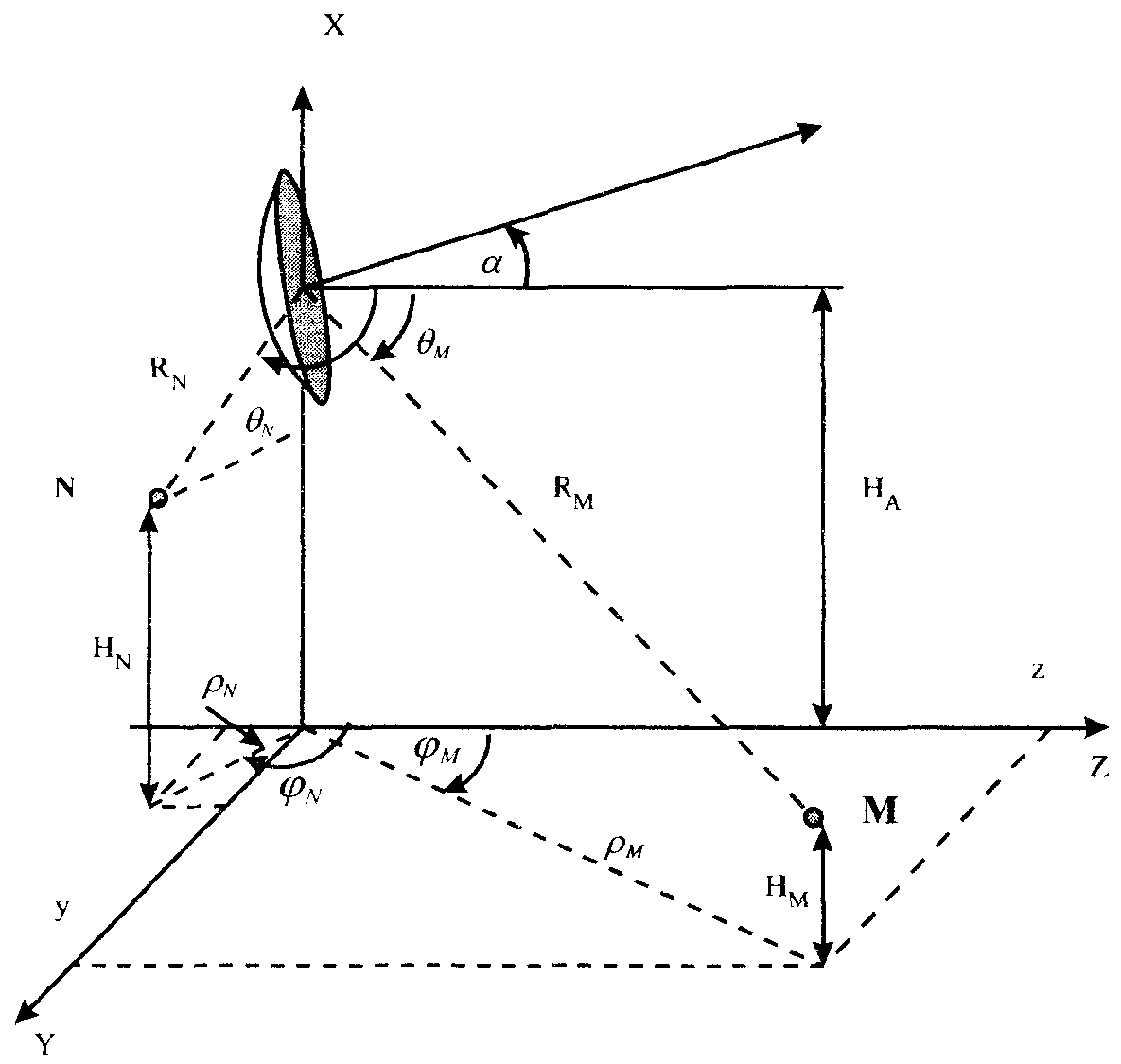 Рис.П2.2. Иллюстрации к примеру расчета ППЭ от антенны ССП. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
