Пособие_Погрешности_Мамонтов_Немова. Методические указания по дисциплинам Теплотехника, Тепломассообмен, Основы экспериментальных исследований
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
4. Построение статистических распределений и критерии оценки Как было показано выше, для построения вероятностной модели процесса необходимо установить закон распределения экспериментальных данных. Для этой цели служат различные критерии, которые позволяют оценить распределение генеральной совокупности данных с определенной вероятностью по конечной выборке. В общем случае применяется следующий алгоритм для оценки статистического распределения. 1. Построение гистограммы. 1.1. Нахождение центра. 1.2. Симметрирование гистограммы. 1.3. Сглаживание. 2. Аппроксимация полученной гистограммы к распределению. 3. Проверка построения по критериям согласия. При построении гистограммы (см. рис. 4.1) выбирается число интервалов 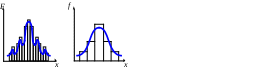 а б Рис. 4.1. Выбор числа Выбор числа Общим для всех методов определения Для нахождения центра распределения рассчитывают 50% квантиль (половина выборки больше, другая половина – меньше этого числа). Эта квантиль может не совпадать со средним значением. Симметрирование гистограммы заключается в выравнивании симметричных столбцов переносом некоторого числа отсчетов. Для оценки нормальности закона распределения используют критерии согласия, наиболее распространенным из которых является критерий Пирсона Здесь  Рис. 4.2. Критерий Пирсона В отличие от распределения Стьюдента критерий Для сравнения двух независимых выборок служит критерий Колмогорова-Смирнова, который позволяет определить относятся ли две независимые выборки к одной генеральной совокупности. При этом нет необходимости строить гистограмму. 5. Построение функциональных зависимостей по экспериментальным данным При анализе экспериментальных данных наиболее распространенными способами задания искомой зависимости 1. Обработка проводится при непосредственном численном использовании массива значений 2. Если количество измерений невелико и разброс значений мал, используется интерполяция (аппроксимация). Зависимость проводится через все точки с координатами 3. При высокой степени полинома отрезок интерполяции разбивается на несколько частей с построением для каждого интерполяционного многочлена. Недостатком является существование разрыва первой производной в точках стыка. 4. Чтобы зависимость имела непрерывные производные используются сплайны – функции, являющиеся многочленами и непрерывные во всей области со своими производными. 5. Для построения функциональной зависимости для однофакторного эксперимента с многократными отсчетами используется метод наименьших квадратов. 5.1. Метод наименьших квадратов Метод используется тогда, когда число точек велико и построение плавной зависимости Пусть приближенная функция, описывающая Задача сводится к отысканию минимума 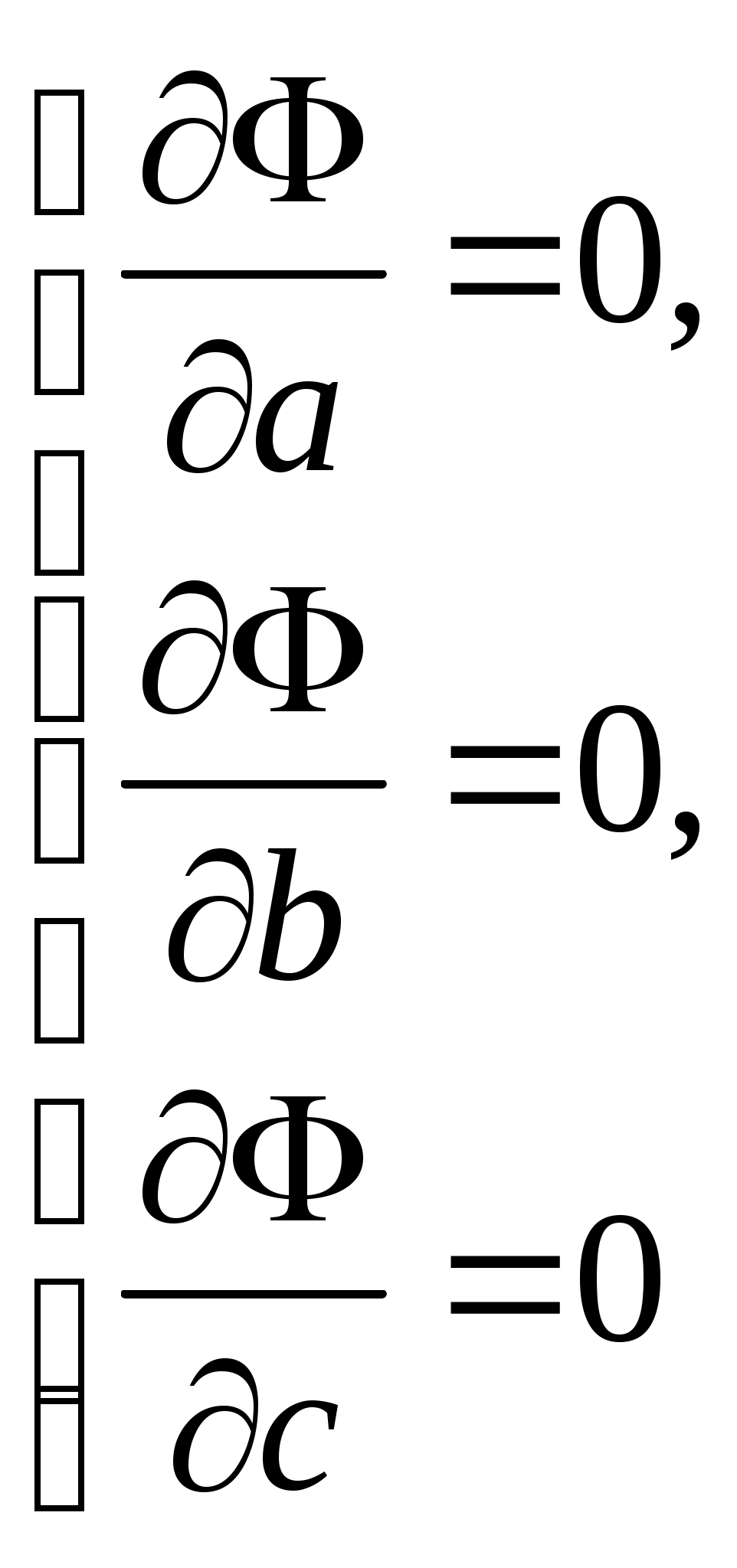 (5.2) (5.2)или 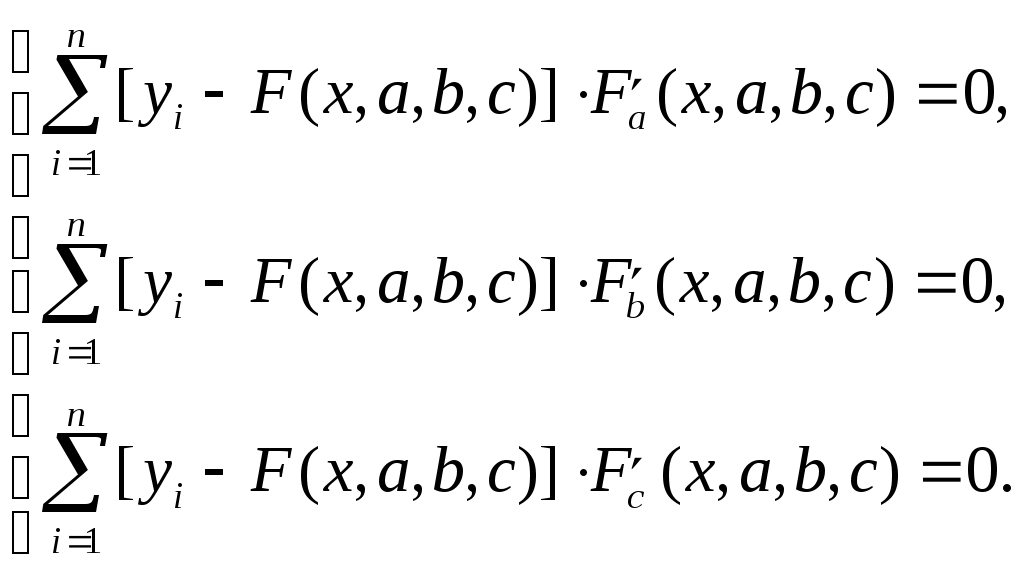 (5.3) (5.3)Решением этой системы относительно параметров Приближенная функция может иметь любой вид: линейная зависимость, парабола, синусоида и т.д. Чаще всего используются алгебраические многочлены не выше третьего порядка. В большинстве случаев используется линейная регрессия, когда 5.2. Быстрые методы построения функциональных зависимостей Одна и та же экспериментальная зависимость может быть описана разными аналитическими выражениями примерно с одинаковой точностью. Например, К математическим моделям, описывающим экспериментальные зависимости, предъявляются требования, заключающиеся в компактности и удобстве их использования, а также в их интерпретируемости. Первое из них заключается в применении в математических моделях алгебраических многочленов, экспоненциальных или тригонометрических функций. Второе требование предполагает знание физической модели явления, которое позволяет выбрать правильную зависимость для его описания. Погрешность в выборе функциональной зависимости называется погрешностью адекватности модели. 5.2.1. Установление графического вида однофакторных зависимостей Наиболее простым экспресс - методом является метод контура. Суть метода заключается в обведении экспериментальных точек плавными линиями (рис. 5.1). При этом некоторые точки могут оказаться вне контура (рис. 5.1. а). Метод используют, когда разброс точек небольшой. (рис. 5.2. б). 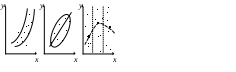 а б в Рис. 5.2. Более строгим экспресс - методом является метод медианных центров (рис. 5.2. в).Для этого область экспериментальных данных разбивается вертикальными линиями на несколько областей, в каждой из которых находится равное количество точек. Затем находятся медианные центры каждой из областей по координатам 5.2.2. Связь коэффициента линейной регрессии, коэффициента корреляции и относительной погрешности Если по результатам однофакторного эксперимента строится линейная регрессия 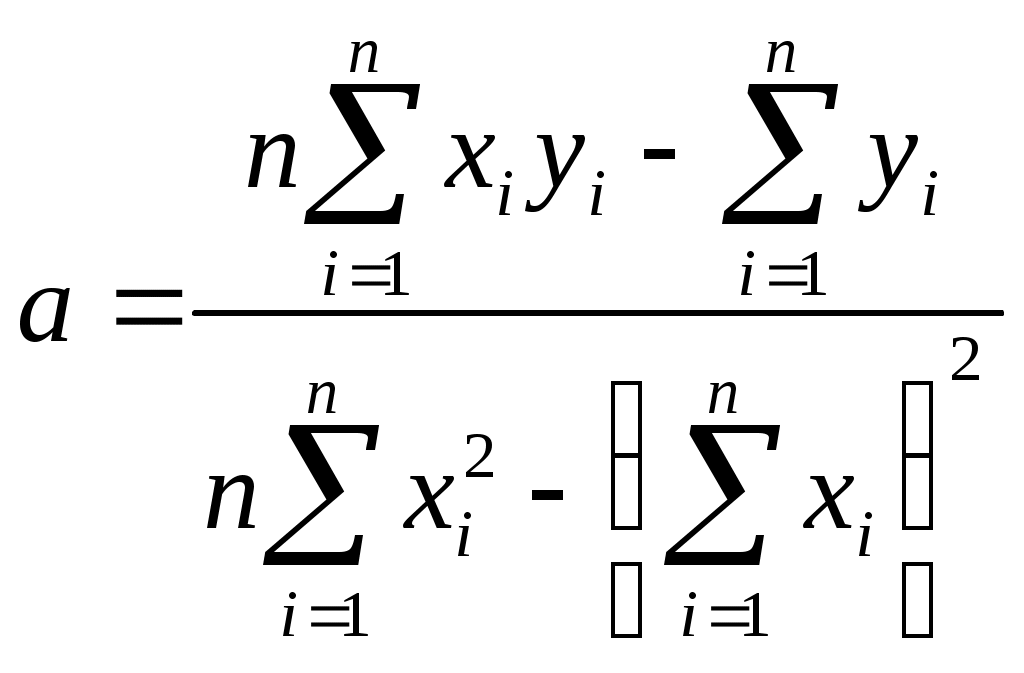 , , 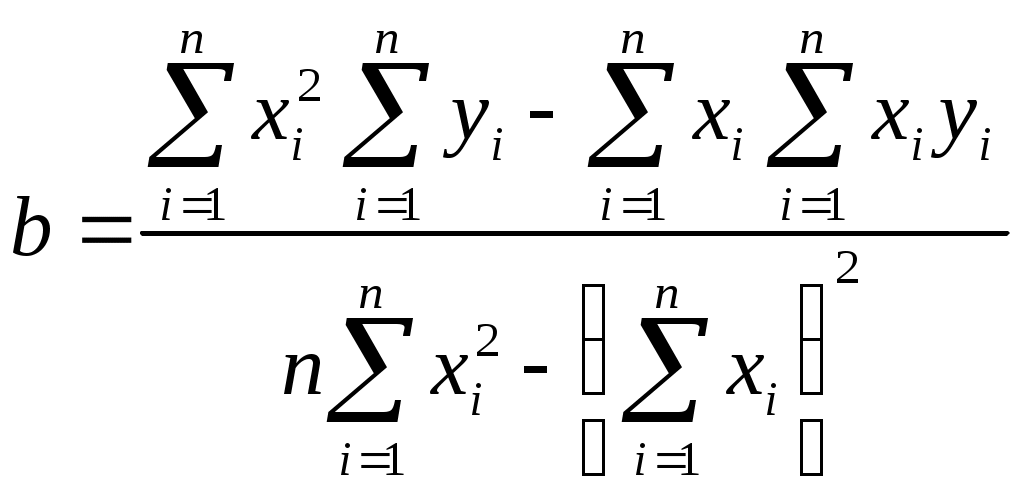 . (5.4) . (5.4)Коэффициент корреляции между 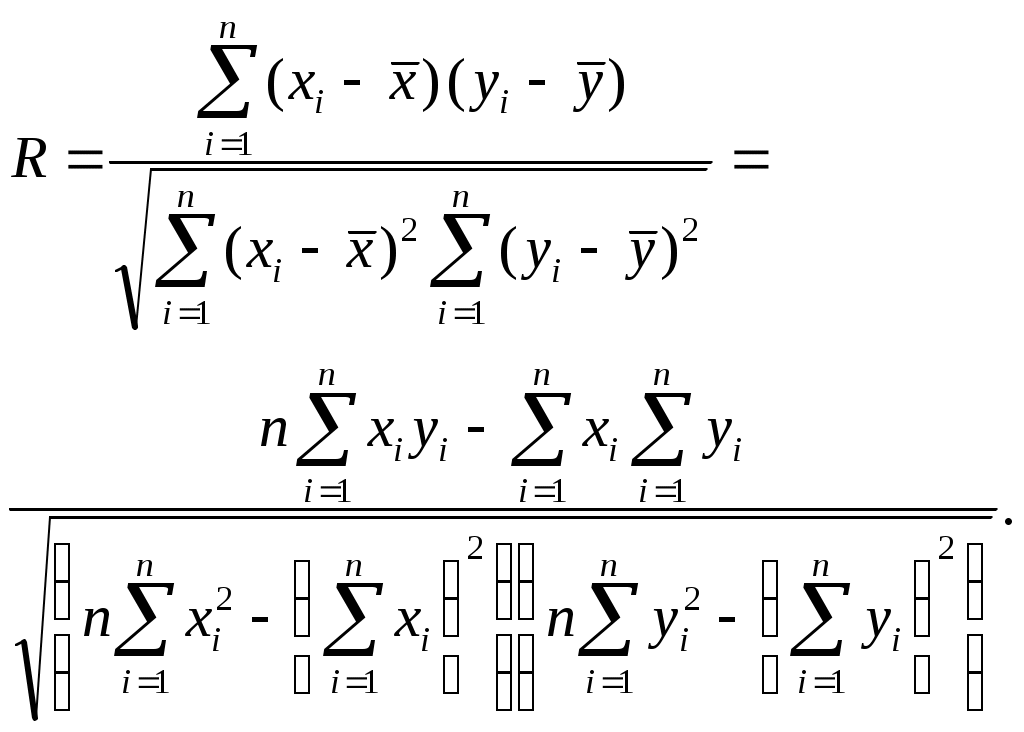 (5.5) (5.5)Сопоставляя это выражение с выражениями для расчета коэффициентов регрессии, получаем 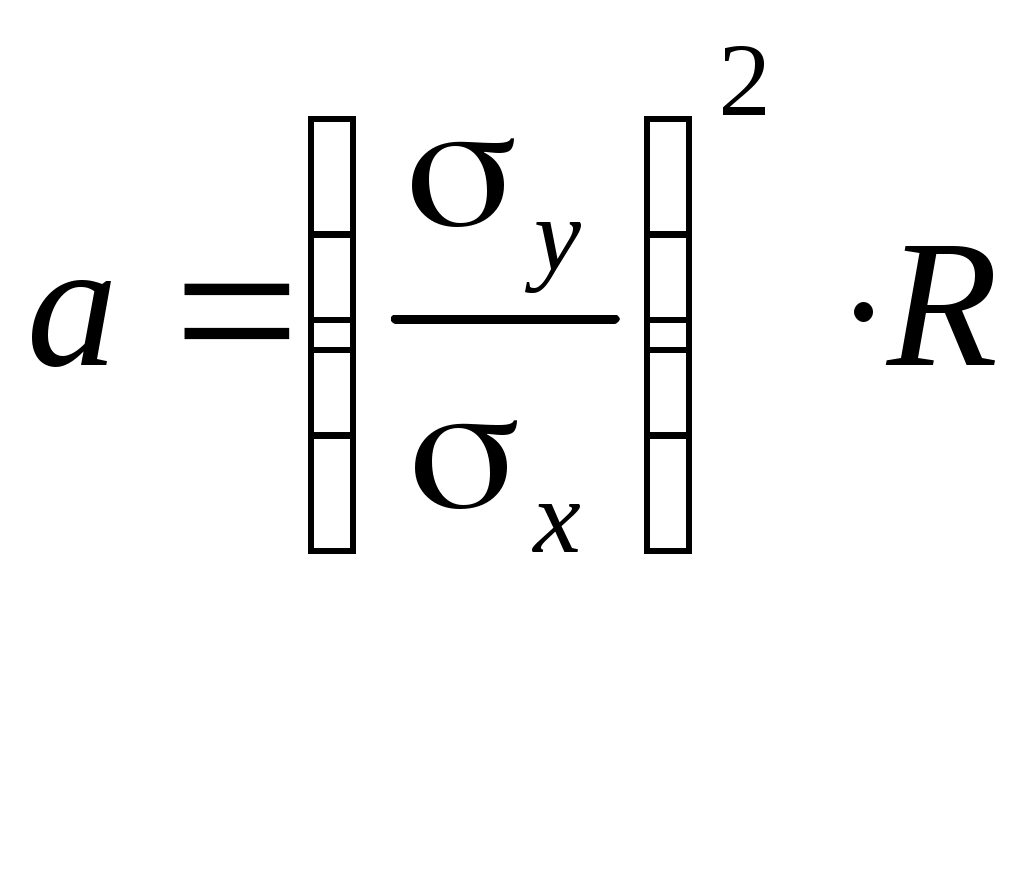 , где , где Отсюда коэффициент корреляции связан с разбросом по осям 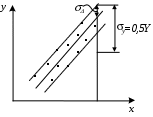 Рис. 5.3. С учетом этого коэффициент корреляции часто определяют как 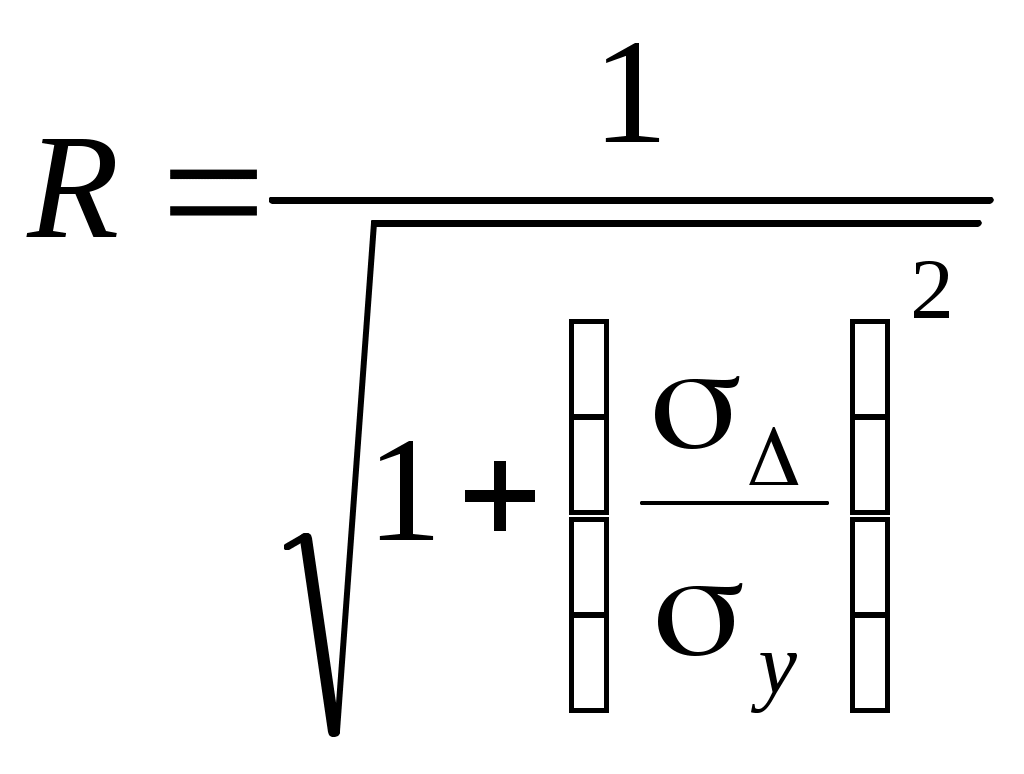 . (5.6) . (5.6)Здесь На практике 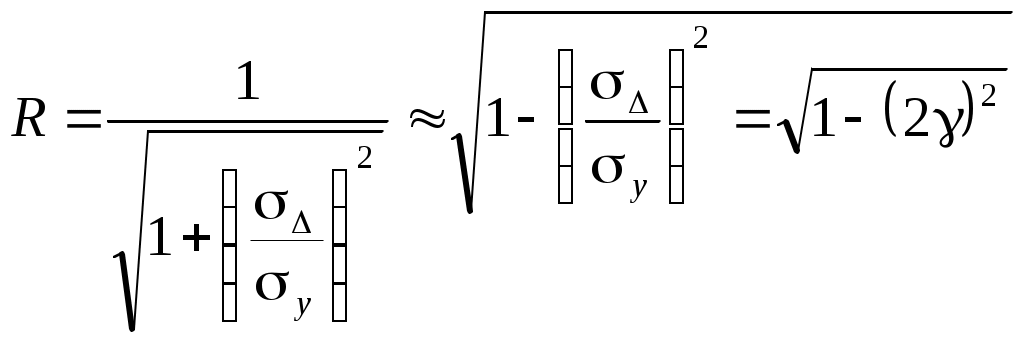 , (5.7) , (5.7)где Эта приближенная формула позволяет для большинства практических расчетов установить связь между коэффициентом корреляции и приведенной погрешностью. Быструю оценку коэффициента корреляции и погрешности исходных данных можно провести с использованием описанного выше метода медианных центров (рис. 5.4). Поле экспериментальных точек разбивается вертикальной линией на две области, в каждой из которых находятся медианные центры. Линия По различию прямых коэффициент корреляции можно оценить следующим выражением (см. рис. 5.4) 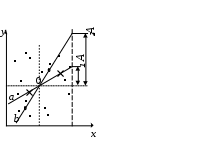 Рис. 5.4. Полученные методом медианных центров регрессионные зависимости будут отличаться от соответствующих зависимостей, полученных методом наименьших квадратов. Различия их будут уменьшаться при увеличении числа измерений при условии подчинения разброса экспериментальных данных нормальному закону распределения. 5.2.3. Сглаживание экспериментальных временных рядов Построение плавных временных зависимостей функции 1. Временные ряды характеризуются значительным количеством отсчетов. 2. Как правило, отсчеты производятся через равные промежутки времени. 3. Зависимость 4. Аппроксимирующую функцию по всей длине временного ряда нельзя описать аналитически. Для однофакторного эксперимента функциональная зависимость Существует множество способов сглаживания временных рядов. Наиболее простыми из них являются метод скользящего среднего и медианное сглаживание. На рисунке 5.5 приведены две зависимости, имеющие одинаковую регулярную составляющую, но различающиеся по случайным составляющим. Во втором случае кроме мелких случайных флуктуаций имеются редкие выбросы со значительной амплитудой. Метод скользящего среднего предполагает выбор некоторого окна усреднения 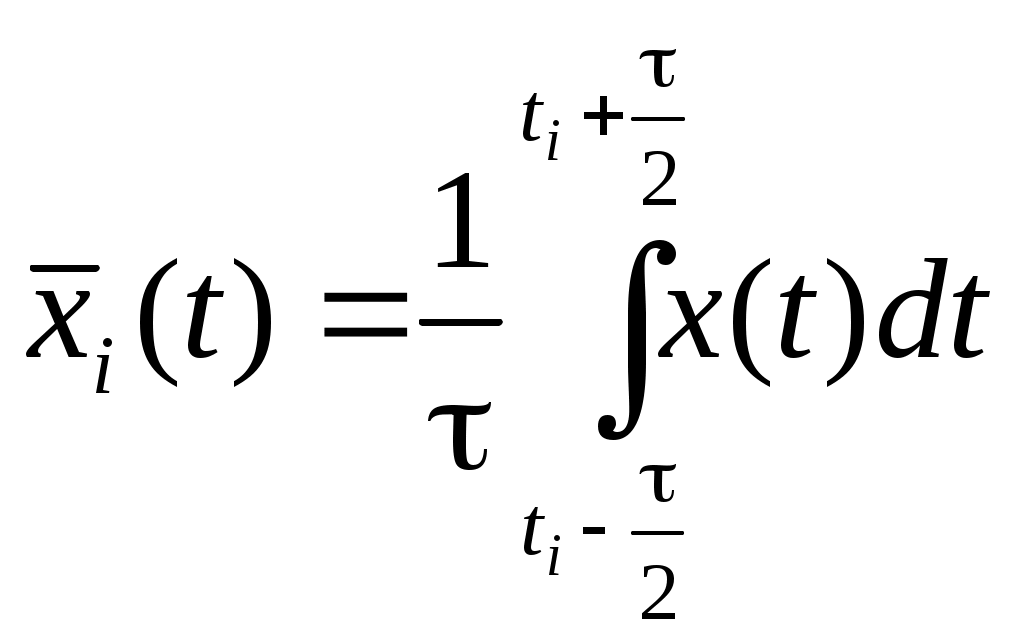 . .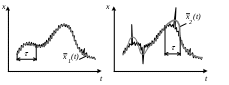 Рис. 5.5. Этот метод позволяет избавиться от высокочастотных флуктуаций, при этом фильтрация высоких частот зависит от длины интервала усреднения Применение метода скользящего среднего к зависимости, имеющей редкие, но значительные выбросы, приводит к ее искажению. Выбросы при попадании в интервал усреднения сильно влияют на среднее значение. В этом случае правомернее использовать метод медианного сглаживания. В этом случае используется не среднее значение функции, а медиана. Правила построения медианы предполагают нахождение медианного центра в области большинства точек, за счет чего выброс в одной из точек будет устранен. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Зайдель А.А. Ошибки измерений физических величин. Ленинград: Наука. 1974. 2. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. Главная редакция физ.-мат. Литературы: Наука. 1970. 104 с. 3. Маркин Н.С. Основы теории обработки результатов измерений. Издательство стандартов: М. 1991. 176 с. 4. Славутский Л.А. Основы регистрации данных и планирования эксперимента. Учебное пособие: изд-во ЧГУ. Чебоксары. 2006. 200 с. 5. Ацюковский В.А. Философия и методология технического комплексирования. М.: Петит. 2006. 211 с. 6. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. Л.:Энергоатомиздат. 1991. 304 с. 7. Интернет-ресурсы. |
