Пособие_Погрешности_Мамонтов_Немова. Методические указания по дисциплинам Теплотехника, Тепломассообмен, Основы экспериментальных исследований
 Скачать 0.82 Mb.
|
|
3. Случайные погрешности Случайную погрешность можно рассматривать как суммарный эффект действия ряда факторов, которые в отдельности нельзя выделить или учесть, так как эффект их действия является незначительным. Закономерность проявления случайных погрешностей учитывается при достаточно большом количестве измерений и с помощью теории вероятностей оценивается их влияние на истинное значение физической величины. В том случае, если погрешность прибора заведомо больше величины случайных погрешностей, присущих данному методу при данных условиях эксперимента, достаточно выполнить измерение один раз (например, при измерении обычной масштабной линейкой длины точно изготовленной детали). Тогда абсолютная погрешность измерения будет равна погрешности прибора. Если, наоборот, определяющей является случайная погрешность, надо уменьшить ее величину с помощью многократных измерений. 3.1 Распределение случайных погрешностей. Закон Гаусса Случайные погрешности подчиняются закономерностям статистического характера. Можно выделить следующие свойства случайных погрешностей. 1. Случайные погрешности не могут превосходить по абсолютному значению определенного предела, который зависит от условий и средств измерения физической величины. 2. При измерениях положительные и отрицательные случайные погрешности встречаются одинаково часто. 3. Среднее арифметическое значение из случайных погрешностей измерений в идентичных условиях одной и той же физической величины стремится к нулю при возрастании числа измерений. 4. Чем больше абсолютное значение погрешности, тем реже такая погрешность встречается в ряду измерений. Это позволяет на практике определить предел, который в конкретных условиях не превосходят случайные погрешности. При соответствии погрешностей вышеперечисленным свойствам считается, что реализуется нормальное распределение погрешностей измерения. Случайные погрешности измерений физической величины характеризуются определенным законом их распределения. Существование такого закона можно обнаружить многократным повторением измерений физической величины. При этом подсчитывается число тех результатов, которые попали в любой заданный интервал. Отношение этого числа к общему числу измерений (  ) называется относительной частотой и при большом количестве измерений является практически постоянным числом для каждого интервала. Это обстоятельство позволяет применить к изучению случайных погрешностей методы теории вероятностей и математической статистики. Если в результате  измерений величины  , проведенных с одинаковой точностью, получен ряд значений:  , то наиболее близким к истинному значению  измеряемой величины является среднее арифметическое значение . (3.1)Среднее арифметическое значение обычно рассматривается как наиболее вероятное значение измеряемой величины. Суммируя абсолютные погрешности (  ), получаем . (3.2)Отсюда  . Второе слагаемое правой части уравнения при больших значениях числа измерений будет равно нулю, так как абсолютные погрешности с равной вероятностью могут принимать как положительные, так и отрицательные значения. В этом случае  . При ограниченном числе измерений  .В практических расчетах значение не известно, поэтому принимается, что находится в каком-то интервале вблизи  и с определенной вероятностью находится этот интервал. В качестве оценки абсолютной погрешности используется величина  , определяющая точность данного измерения. Так как сумма отклонений  равна нулю, то для оценки погрешностей используют или абсолютные величины значения разностей ( ), или их квадраты. Такие оценки называют средней арифметической погрешностью  . . (3.3)Средняя арифметическая погрешность определяет пределы, в которых лежит большая часть значений измеряемой величины. Следовательно, значение с достаточно большой вероятностью попадает в интервал от  до  . Результаты измерений можно записать в виде  . Чем меньше интервал, в котором находится значение , тем точнее измеренная величина. Частоты появления какого-либо значения величины 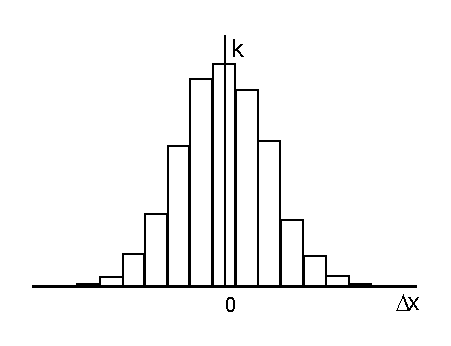 при многократных измерениях графически выражаются в виде ступенчатой кривой (гистограммы). С увеличением числа измерений гистограмма переходит в кривую, характеризующую плотность распределения вероятности нахождения величины  в интервале  . Рис. 3.1 Распределение случайной величины есть совокупность всех возможных значений случайной величины и соответствующих им вероятностей. Соответственно законы распределения случайной величины устанавливают соответствие между случайной величиной и возможным значением ее вероятности. 3.2. Вероятностная оценка случайной погрешности Для характеристики частоты появления различных значений случайной величины теория вероятностей позволяет использовать закон распределения вероятностей различных значений этой величины. Вероятность P того, что случайная величина 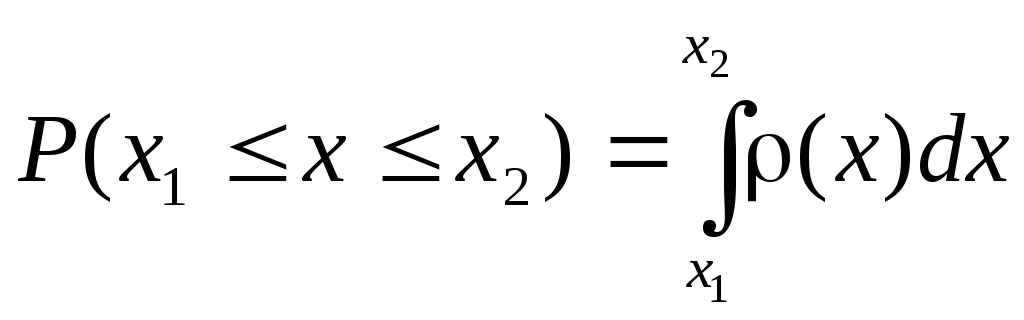принимает значения в некотором интервале  определяется выражением , (3.4)где  называется плотностью распределения вероятности случайной величины х или статистическим распределением. Функция удовлетворяет условию нормировки  , поскольку находится в интервале  с вероятностью, равной единице. Среднее значение случайной величины с учетом ее статистического распределения можно вычислить из зависимости . (3.5)Если из генеральной совокупности всех возможных значений случайной величины осуществляется конечная выборка дискретных значений  , то расчет среднего значения  соответствует определению среднего по формуле (1) при условии  . То есть, необходимо знать статистическое распределение данных даже для оценки точности вычисления среднего значения. Координата центра распределения определяет положение случайной величины на числовой оси. Так как распределения погрешностей результатов измерений обычно являются симметричными, то центр распределения чаще всего определяется как центр симметрии распределения. Моменты распределения. Для описания различных свойств распределений используются параметры законов распределения или моменты. Моменты, найденные без исключения систематической составляющей, называются начальными, а найденные для центрированных распределений – центральными. Центральный момент k-го порядка для непрерывной случайной величины выражается интегралом  . (3.6)Здесь  - первый начальный момент или математическое ожидание (координата центра распределения, найденная как центр тяжести распределения).  - дисперсия случайной величины, характеризует рассеяние отдельных ее значений от центра распределения.  . Для наглядной характеристики рассеяния используют квадратный корень из дисперсии, который называется средним квадратичным отклонением (СКО) и имеет размерность случайной величины.  . Для конечной выборки СКО рассчитывают по формуле  . (3.7)Эта формула не учитывает форму распределения, однако получила широкое распространение вследствие следующих причин: - простая оценка рассеяния случайных величин; - при экспериментальных измерениях значения случайных величин имеют близкое к нормальному (гауссову) распределение.  - третий центральный момент – характеризует асимметрию распределения. Для симметричных распределений он равен нулю. Для характеристики асимметрии используется безразмерный коэффициент, равный третьему моменту, деленному на куб СКО  . 3.3. Нормальный закон распределения В большинстве случаев считается, что случайные погрешности экспериментальных измерений имеют нормальное (гауссово) статистическое распределение (закон Гаусса). Пусть случайная величина 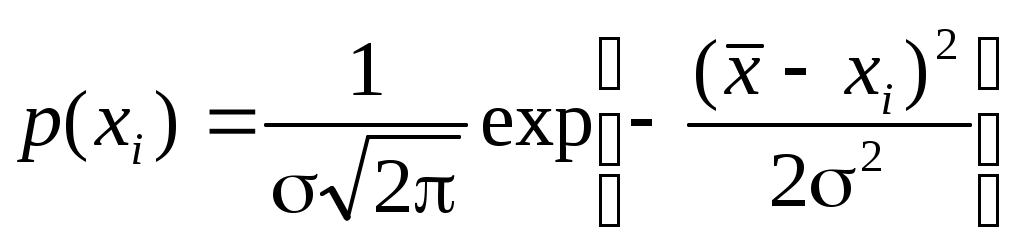 представляет собой сумму случайных величин  , т.е.  . При условии статистической независимости , их произвольном распределении и  их сумма имеет нормальное распределение с плотностью вероятности  . (3.8)Так как закон Гаусса характеризуется средним значением случайной величины и дисперсией  , то среднее значение случайной величины есть абсцисса оси симметрии кривой, а показывает как убывает плотность распределения вероятности с увеличением абсолютного значения погрешности. Кривая распределения имеет максимум  при  . Следовательно, наиболее вероятным значением величины является среднее значение. Дисперсия определяется полушириной кривой распределения 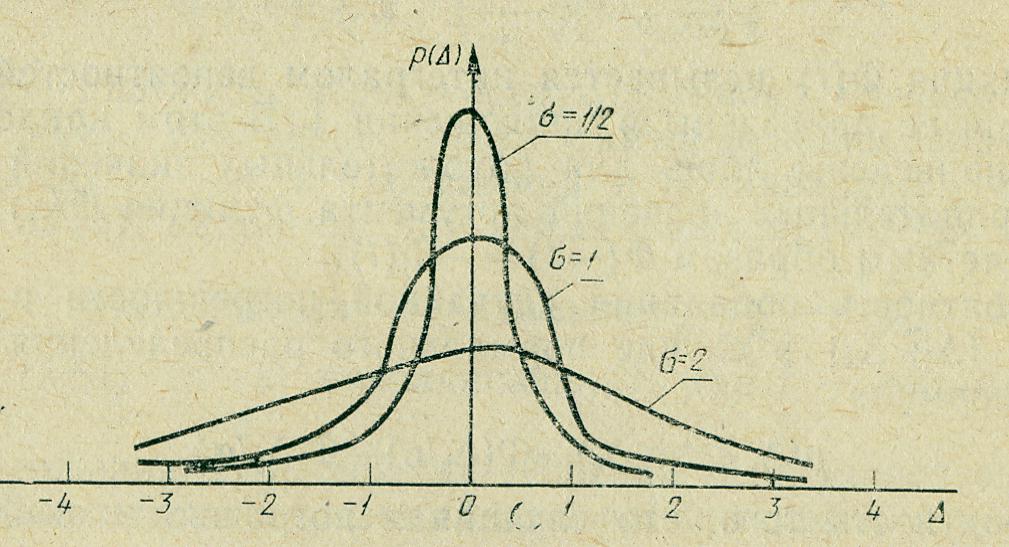 и по теории вероятностей равна  - среднему квадрату отклонения результатов отдельных измерений от их среднего арифметического значения по всему распределению.  при постоянных значениях измеряемой величины.  Рис. 3.2. На рисунке 3.2 показаны кривые нормального распределения при различных значениях дисперсии  . При уменьшении параметра кривая сжимается вдоль оси  и вытягивается вдоль оси  . Следовательно, чем меньше , тем быстрее убывает плотность распределения с возрастанием  .Вероятность  попадания в интервал  графически изображается площадью криволинейной трапеции под кривой распределения вероятностей (рис.3.2). Из этого рисунка также видно, что чем меньше , тем меньше разброс погрешностей относительно нуля.Физический смысл нормального статистического распределения заключается в том, что если случайная величина зависит от большого числа случайных факторов, то она имеет нормальное распределение независимо от характеристик каждого из факторов. Формула, описывающая закон Гаусса выводится с учетом следующих предположений. 1. Ошибки измерений могут принимать непрерывный ряд значений. 2. При большом числе наблюдений ошибки разного знака, но одинаковой величины встречаются одинаково часто. 3. Частота появления ошибок уменьшается с увеличением величины ошибки (большие ошибки наблюдаются реже малых). Достаточно строго эти условия не выполняются. Однако в экспериментах, где погрешности невелики, нормальный закон распределения случайных погрешностей хорошо согласуется с опытными данными. Вероятность попадания случайной погрешности в симметричный интервал при нормальном распределении может быть вычислена по формуле:  ,где 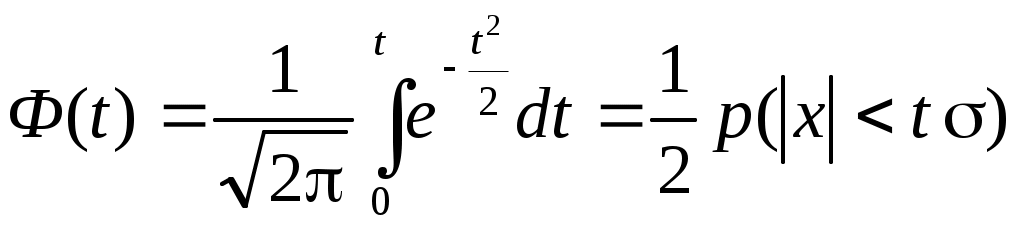 . (3.9)Функция  называется функцией Лапласа или интегралом вероятностей,  . Значения функции Лапласа приведены в специальных таблицах. Вероятность попадания случайной погрешности в любой интервал  при нормальном распределении вычисляется по формуле . (3.10)Вероятность того, что случайная погрешность выйдет за границы  равна . (3.11)Эти значения вероятностей также приводятся в таблицах. Вероятность выхода случайной погрешности за предел  составляет величину, равную 0.0027. То есть, вероятность так мала, что выход за указанные пределы практически невозможен. В теории ошибок это правило (правило трех сигм) показывает, что случайные погрешности измерения ограничены по абсолютной величине значением .Таким образом, для известной величины надежность равна 0.9973 независимо от количества экспериментов. Такая же надежность в случае неизвестной величины достигается при числе измерений не менее 150. Надежностью результата серии измерений называется вероятность  того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Доверительный интервал есть интервал, в который по определению попадает истинное значение измеряемой величины с заданной вероятностью. Естественно, что величина надежности зависит от количества измерений и величины задаваемой погрешности. Если доверительный интервал увеличивается, то возрастает надежность того, что истинное значение попадает в данный интервал. Высокая степень надежности необходима при проведении ответственных измерений. При этом или выбирается большой доверительный интервал, или измерения ведутся с большой точностью. При проведении большинства измерений доверительная вероятность составляет 0.90-0.95. При многократных измерениях, когда необходимо построить зависимость  при условии, что каждому значению соответствует набор значений , поступают следующим образом. Для каждого значения в определенном интервале по точкам находится среднее значение  и рассчитывается среднеквадратичное отклонение  , где  . Следует отметить, что определение СКО не является лучшим способом оценки погрешностей. Однако его используют на практике потому, что эта оценка легко рассчитывается аналитически. Для того, чтобы определить полосу погрешностей искомой зависимости считают, что при данном принимает значение в определенном доверительном интервале с необходимой вероятностью. Для нормального распределения применяют квантильные оценки. Квантили – прямые  , делящие плотность вероятности на определенные части, например, 50-, 25- и 5-процентные (рис. 3.3.).  Рис. 3.3. При предположении равномерного распределения погрешностей квантилей делят график плотности вероятности на  частей. Если отбросить крайние значения , тогда в диапазон [ ] величины попадают с вероятностью  . На практике часто кроме крайних значений отбрасывается определенное число  . В этом случае  . Из этого выражения следует, что при фиксированной доверительной вероятности  можно определить необходимое число отсчетов  .В таблице 3.1 приведены рассчитанные по этой формуле величины n для заданных значений при  .Таблица 3.1
Обычно для статистических оценок используется объем выборки, соответствующий  . Для значений  требуется слишком большая выборка.СКО при вычислении среднего зависит от числа отсчетов  , то есть при усреднении величины по измерениям рассеяние данных уменьшается в  раз. Для оценки доверительного интервала с учетом вероятности необходимо учесть статистическое распределение . Распределение средней величины  вне зависимости от распределения исходных данных соответствует нормальному закону распределения при  . Поэтому переход от оценки СКО  к оценке доверительного интервала с доверительной вероятностью осуществляется с помощью зависимости  , (3.12)где  - нормированная квантиль нормального распределения, соответствующая . Физический смысл величины заключается в зависимости от значения выборки доверительного интервала по отношению к СКО. Доверительному интервалу необходимо поставить в соответствие или , или уровень значимости, равный  . Значения для нормального распределения при разных уровнях значимости (выборка свыше 30) приведены в таблице 3.2.Таблица 3.2
Величина 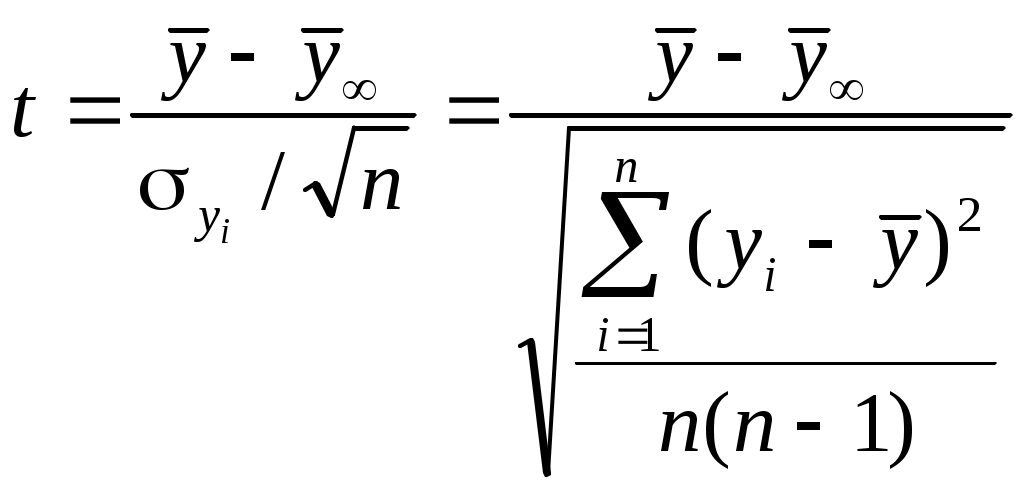определяется следующим образом . (3.13)Статистическое распределение известно как распределение Стьюдента.Распределение Стьюдента. Плотность вероятности этого распределения описывается с помощью специальных функций 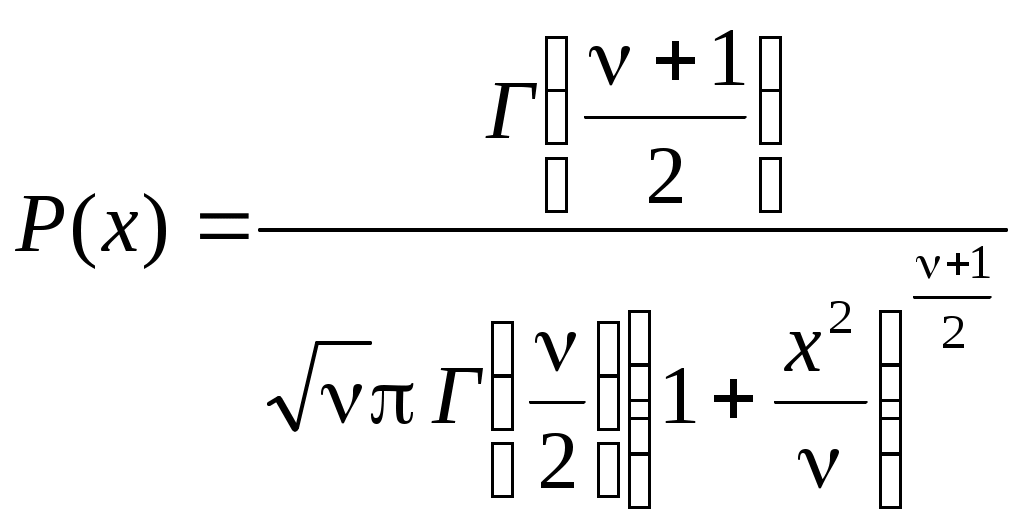 , (3.14)где  определяется числом степеней свободы . Гамма-функция  обладает следующими свойствами: ;  ;  На рисунке 3.4 показано распределение Стьюдента при  (кривая 2) и нормальное распределение (кривая 1). Распределение Стьюдента симметрично и шире нормального. Оно описывает отклонения среднего значения , рассчитанного по малой выборке, от среднего значения генеральной совокупности  . При  распределение Стьюдента совпадает с нормальным распределением.  Рис. 3.5. Значения при вычислении доверительного интервала для конкретной выборки находится из справочной литературы, т.к. распределение Стьюдента широко табулировано. В таблице 3 приведены величины для значений и уровня значимости 0.1 и 0.05.Таблица 3.3
Из таблицы видно, что при значениях  значительно возрастает величина и доверительный интервал в несколько раз превышает СКО (3.12). При  отличие квантили от ее значения при нормальном распределении не превышает 30%. Поэтому распределение Стьюдента используется для такого объема выборки. |
