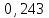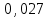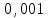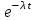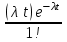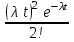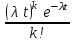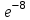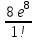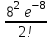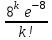МР_к_ЛПЗ_по_ОП.01_09.02.02. Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
Пропускная способность непрерывного каналаПусть сигнал на выходе канала представляет собой сумму полезного сигнала и шума , т.е. , причем и статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной . Тогда в соответствии с теоремой Котельникова (см. п. 1.5) функции , и можно представить совокупностями отсчетов , , и , , где . При этом статистические свойства сигнала можно описать многомерной ПРВ , а свойства шума – ПРВ . Пропускная способность непрерывного канала определяется следующим образом:
где – количество информации о какой-либо реализации сигнала длительности T, которое в среднем содержит реализация сигнала той же длительности , а максимум ищется по всем возможным распределениям . Когда сигнал на входе канала имеет нормальное распределение и отсчеты независимы величина максимизируется [6]. Поэтому пропускная способность гауссовского канала с дискретным временем, рассчитанная на единицу времени, с учетом (4.16) может быть записана в виде
Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется числом импульсов, передаваемых в секунду, и отношением сигнал/шум ( ). С учетом взаимосвязи скорости передачи информации и полосы частот непрерывного канала от (4.17) можно перейти к формуле Шеннона, которая устанавливает связь пропускной способности гауссовского канала с полосой пропускания непрерывного канала и отношением мощности сигнала к мощности помехи:
График отношения изображен на рис. 4.6. Заметим, что при малом отношении
а пропускная способность канала связи прямо пропорциональна этому отношению. 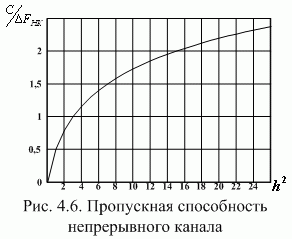 При большом отношении в (4.18) можно пренебречь единицей и считать, что
т.е. зависимость пропускной способности непрерывного канала от отношения сигнал/шумлогарифмическая. Пропускная способность канала, как предельное значение скорости безошибочной передачи информации, является одной из основных характеристик любого канала. Определим пропускную способность стандартного канала тональной частоты, имеющего границы эффективно передаваемых частот кГц, среднюю мощность сигнала на выходе 56 мкВт при средней мощности помехи 69000 пВт. Согласно (4.18), при заданных параметрах
Для непрерывных каналов справедлива теорема Шеннона, согласно которой сообщения дискретного источника могут быть закодированы и переданы по непрерывному каналу так, что вероятность ошибочного декодирования принятого сигнала будет меньше наперед заданной положительной величины , если производительность источника меньше пропускной способности непрерывного канала. Для типовых непрерывных каналов многоканальной связи основные технические характеристики и пропускная способность, вычисленная по формуле Шеннона (4.18), при отношении сигнал/шум 20 дБ, приведены в табл. 4.4. Зная пропускную способность канала и информационные характеристики сообщений (табл. 4.5), можно определить, какие сообщения (первичные сигналы) можно передавать по заданному каналу. Таблица 4.4. Характеристики типовых каналов многоканальной связи
Таблица 4.5. Производительность источников сообщений
Например, первичный сигнал телевизионного вещания имеет (табл. 4.5) и поэтому не может быть передан ни по одному из типовых непрерывных или цифровых каналов без потери качества. Следовательно, для передачи сигнала телевизионного вещания требуется создание специальных каналов с более высокой пропускной способностью или снижение скорости цифрового потока. Задачи 1. Число символов алфавита m = 4. Вероятности появления символов равны соответственно p1 = 0,15; p2 = 0,4; p3 = 0,25; p4 = 0,2. Длительности символов t1 = 3с; t2 = 2с; t3 = 5с, t4 = 6с. Чему равна скорость передачи сообщений, составленных из таких символов? 2. Сообщения составлены из пяти качественных признаков (m = 5). Длительность элементарной посылки t = 20мс. Определить, чему равна скорость передачи сигналов и информации. 3. Определить пропускную способность бинарного канала связи, способного передавать 100 символов 0 или 1 в единицу времени, причем каждый из символов искажается (заменяется противоположным) с вероятностью р = 0,01. 4. Имеются источник информации с энтропией в единицу времени H(Х) = 100 дв.ед. и два канала связи; каждый из них может передавать в единицу времени 70 двоичных знаков (0 или 1); каждый двоичный знак заменяется противоположным с вероятностью р = 0,1. Требуется выяснить, достаточна ли пропускная способность этих каналов для передачи информации, поставляемой источником. 5. Чему равна пропускная способность симметричного канала, если источник вырабатывает сигналы со скоростью 2 знака в секунду, закодированные кодом с основанием m = 10, а вероятность ложного приема р = 0,3? 6. Сообщения составлены из алфавита Х = (х1, x2, x3). Вероятности появления символов алфавита 0,7; 0,2; 0,1 соответственно. Помехи в канале связи заданы следующей канальной матрицей: 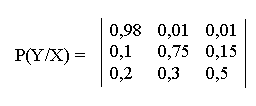 Определить скорость передачи информации, если время передачи одного символа t1 = 0,02с. 7. Чему раина пропускная способность канала связи, описанного канальной матрицей: 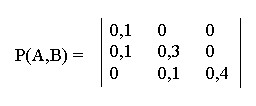 если известно, что на выходе источника сообщений символы вырабатываются со скоростью 100 знаков в секунду? 8. Определить максимально возможную скорость передачи информации по радиотехническому каналу связи пункта управления с телеуправляемой ракетой, если полоса пропускания канала связи равна 3 МГц, а минимальное отношение сигнал-шум по мощности в процессе наведения ракеты на цель равно 3. 9. Определить полосу пропускания канала передачи телевизионного черно-белого изображения с 5х105 элементами, 25 кадрами в секунду и 8 равновероятными градациями яркости для отношения P/N = 15 при условии, что изображение может принимать наиболее хаотичный вид «белого шума». Отчет Отчет должен быть оформлен в текстовом редакторе и содержать: наименование работы; цель работы; задание; последовательность выполнения работы; ответы на контрольные вопросы; вывод о проделанной работе. Контрольные вопросы 1. Что такое пропускная способность канала передачи информации? Чем отличается пропускная способность от скорости передачи информации по каналу связи? 2. Чем отличается информационная скорость передачи от технической, и в каких единицах эти скорости измеряются? 3. Как изменяется пропускная способность дискретного канала связи при воздействии на канал помех. 4. Сформулируйте основную теорему Шеннона о кодировании для канала без помех. 5. Сформулируйте и поясните теорему Шеннона о кодировании для канала с помехами. 6. Приведите выражение пропускной способности для дискретного канала без помех и с помехами. 7. Сформулируйте и поясните теорему отсчетов (Котельникова) 8. Какие параметры влияют на объем сигнала. 9. От чего зависит пропускная способность непрерывного канала связи. 10. Назовите условия согласования источников информации с пропускной способностью непрерывных каналов связи. 11. Какова скорость отображения информации приемным устройством отображения информации. Лабораторная работа №4 Тема: Составление закона распределения вероятностей. Цель: научиться составлять законы распределения вероятностей. Время выполнения: 2 часа Оборудование: ПК. Программное обеспечение: операционная система, калькулятор. Теоретические основы Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными ненулевыми вероятностями. Число возможных значений может быть конечным или бесконечным (счетным). Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Закон распределения может быть задан одним из следующих способов. Таблицей
где 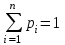 . .Аналитически 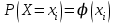 . Например: . Например:а) биномиальное распределение 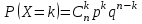 , 0р1, k=0, 1, 2, …, n; , 0р1, k=0, 1, 2, …, n;б) распределение Пуассона 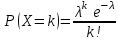 , 0, k=0, 1, 2, … . , 0, k=0, 1, 2, … .С помощью функции распределенияF(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т. е. 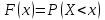 . . СвойстваF(x): 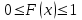 ; ;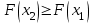 , если , если 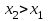 ; ;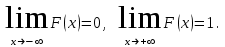 Закон распределения может быть задан графически - многоугольником распределения (см. пример 1). Числовые характеристики дискретных случайных величин Математическое ожидание 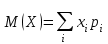 ; ;Дисперсия 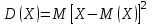 или или 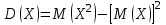 ; ;Среднее квадратическое отклонение(X)= 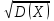 . .Для биномиального распределения М(X)=np, D(X)=npq. Для распределения Пуассона М(X)=,D(X)= . Пример 1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить её график. Найти М(X), D(X), (X). Решение: Дискретная случайная величина Х (число отказавших элементов в одном опыте) имеет следующие возможные значения: х1=0 (ни один из элементов устройства не отказал), х2=1 (отказал один элемент), х3=2 (отказало два элемента) и х4=3 (отказали три элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1 (следовательно, q=1–0,1=0,9), получим: Р3(0)=q3=0,93=0,729; 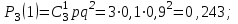 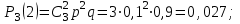 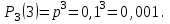 Контроль: 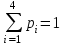 ; 0,729+0,243+0,027+0,001=1. ; 0,729+0,243+0,027+0,001=1. Искомый биномиальный закон распределения Х: 
Для построения многоугольника распределения строим прямоугольную систему координат. По оси абсцисс откладываем возможные значения хi, а по оси ординат – соответствующие им вероятности рi. Построим точки М1(0;0,729), М2(1;0,243),М3(2;0,027), М4(3;0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения (Рис.1). 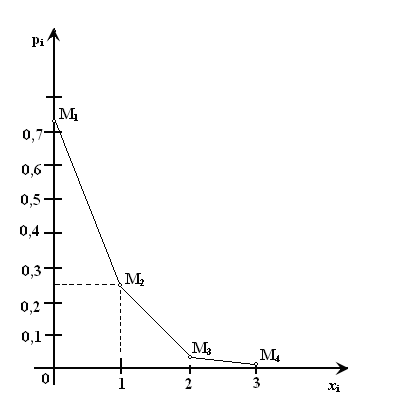 Рис.1 Найдем функцию распределения F(x)=Р(Хх). Для 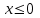 имеем F(x)=Р(Х0)=0; имеем F(x)=Р(Х0)=0; для 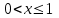 имеем F(x)=Р(Х1)=Р(Х=0)=0,729; имеем F(x)=Р(Х1)=Р(Х=0)=0,729;для 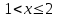 F(x)=Р(Х2)=Р(Х=0)+Р(Х=1)=0,729+0,243=0,972; F(x)=Р(Х2)=Р(Х=0)+Р(Х=1)=0,729+0,243=0,972; для 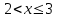 F(x)=Р(Х3)=Р(Х=0)+Р(Х=1)+ Р(Х=2)=0,972+0,027=0,999; F(x)=Р(Х3)=Р(Х=0)+Р(Х=1)+ Р(Х=2)=0,972+0,027=0,999;для х3 будет F(x)=1, т. к. событие достоверно. 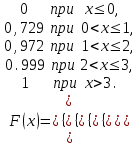 . .График этой функции приведен на Рис. 2. 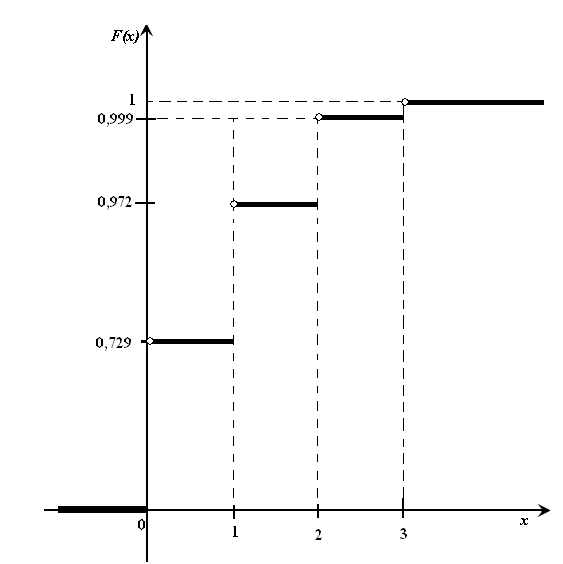 Рис. 2 Для биномиального распределения М(X)=np=30,1=0,3; D(X)=npq=30,10,9=0,27; (X)= 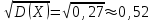 . .Пример 2. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения случайной величины X – числа стандартных деталей среди отобранных. Найти М(X), D(X). Решение: Случайная величина Х – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х1=0; х2=1; х3=2. Найдем вероятности возможных значений Х по формуле (пример 2) 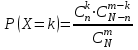 (N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим: (N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим: 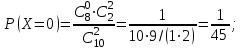 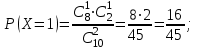 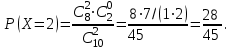 Составим искомый закон распределения:
Контроль: 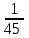 + +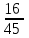 + +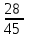 =1. =1. 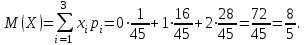 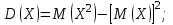 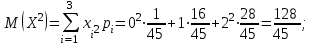 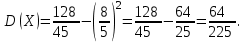 Пример 3. В устройстве независимо друг от друга выходят из строя три элемента. Вероятность выхода из строя первого элемента – 0,3, второго – 0,2, третьего – 0,4. Составить закон распределения случайной величины Х – числа вышедших из строя элементов. Решение: случайная величина Х имеет следующие возможные значения: х1=0, х2=1, х3=2, х4=3. р1=0,3,q1=1- р1=0,7, р2=0,2, q2=1- р2=0,8, р3=0,4, q3=1- р3=0,6. P(X=k) вычисляем по следующим формулам (см. пример 4) 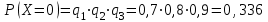 ; ; 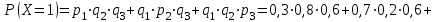 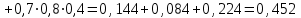 ; ;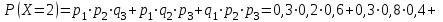 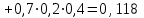 ; ;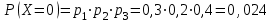 . .Контроль: 0,336+0,452+0,118+0,024=1.
Пример 4. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно двум. Составить закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты. Найти М(X), D(X). Решение: Поток заказов на такси можно считать простейшим, т. е. обладающим стационарностью, «отсутствием последствия» и ординарностью. Интенсивностьпотока (среднее число событий появляющихся в единицу времени) =2. Вероятность появления k событий простейшего потока за время t=4 определяется формулой Пуассона 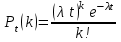 , для данной задачи , для данной задачи 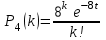 . Совокупность возможных значений X есть счетное множество, т.е. х1=0, х2=1, … , хk=k+1, …; тогда закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты принимает вид: . Совокупность возможных значений X есть счетное множество, т.е. х1=0, х2=1, … , хk=k+1, …; тогда закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты принимает вид:
или
Воспользовавшись таблицей 3 приложения, окончательно получим:
Наивероятнейшее число заказов такси за 4 минуты можно определить по получившемуся закону распределения ( значения х, при которых р максимально): k0=7, k0=8. Для простейшего потока событий: математическое ожидание 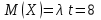 , дисперсия , дисперсия 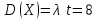 . .Пример 5.
Решение: Закон распределения V=2Y получается из распределения Y путем умножения всех значений yi на 2. Получаем:
. Для составления закона распределения случайной величины Z вычислим все ее возможные значения по формуле 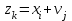 , , 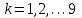 , , 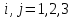 . .Соответствующие данным значениям 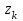 вероятности вероятности 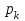 можно вычислить по формуле умножения вероятностей можно вычислить по формуле умножения вероятностей 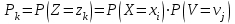 , т. к. события , т. к. события 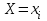 и и 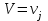 - независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие { - независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие {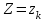 } ={совместное наступление событий } ={совместное наступление событий 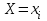 и и 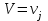 }). Тогда распределение Z принимает вид }). Тогда распределение Z принимает вид
Рассмотрим значения 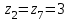 . События . События 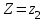 и и 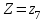 несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей 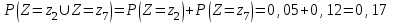 Искомый закон распределения случайной величины Z получается после размещения zk по возрастанию.
Математическое ожидание M(Z) и дисперсию D(Z) можно найти по формулам: 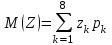 ; ; 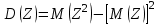 , где , где 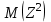 = =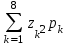 . .Рассмотрим другой способ. M(Z) иD(Z) можно найти через М(Х), М(Y), D(Х), D(Y). 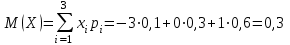 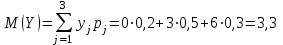 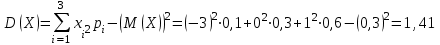 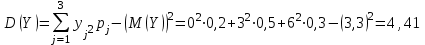 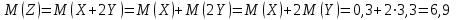 , ,т. к. математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания. 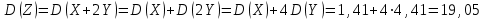 , ,т. к. дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат. Пример 6. Стрелок ведет стрельбу с вероятностью попадания в цель 0,8 при каждом выстреле. Стрельба ведется до первого попадания, но делается не более 3 выстрелов. Составить закон распределения случайной величины Х, если: а) Х – число промахов; б) Х – число попаданий; в) Х – число произведенных выстрелов. Решение: Вероятность попадания р=0,8; вероятность промаха q=1-p=0,2. а) Случайная величина Х – число промахов при трех выстрелах – имеет следующие возможные значения:  ; ;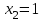 ; ;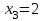 ; ;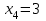 . .Событие Х=0 равносильно попаданию с первой попытки, следовательно, Р(Х=0)=р=0,8. Событие Х=1 равносильно попаданию со второй попытки, т. е. совместному наступлению двух событий: промаха и попадания; следовательно, Р(Х=1)=q 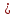 р=0,2 р=0,2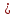 0,8=0,16. 0,8=0,16.Событие Х=2 равносильно попаданию с третьей попытки, т. е. Р(Х=2)=q 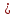 q q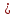 р=0,2 р=0,2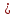 0,2 0,2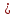 0,8=0,032. 0,8=0,032.Событие Х=3 означает отсутствие попаданий, Р(Х=3)=q 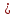 q q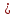 q= q=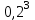 =0,008. =0,008.Искомый закон распределения Х:
б) Случайная величина Х – число попаданий – имеет следующие возможные значения:  (допущено три промаха); (допущено три промаха);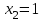 (произошло попадание с первой, второй или третьей попытки). (произошло попадание с первой, второй или третьей попытки).Тогда Р(Х=0)= 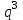 = =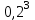 =0,008; =0,008;Р(Х=1)= р+q 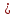 р+q р+q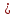 q q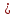 р=0,8+0,16+0,032=0,992 р=0,8+0,16+0,032=0,992или Р(Х=1)=1-Р(Х=0)=1-0,008=0,992. Искомый закон распределения Х:
в) Случайная величина Х – число произведенных выстрелов – имеет следующие возможные значения: 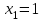 ; ;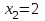 ; ;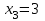 . . Событие Х=1 равносильно попаданию с первой попытки, т. е. Р(Х=1)=р=0,8. Событие Х=2 равносильно попаданию со второй попытки, т. е. Р(Х=2)=q 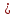 р=0,16. р=0,16.Событие Х=3 означает, что либо произошло попадание с третьей попытки, либо было три промаха. Тогда Р(Х=3)=q 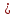 q q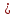 р+q р+q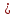 q q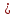 q=0,032+0,008=0,04. q=0,032+0,008=0,04.Искомый закон распределения Х:
Задачи Вариант 1. Производятся последовательные независимые испытания приборов на надёжность. Каждый следующий прибор испытывается лишь в том случае, если предыдущий оказался надежным. Построить закон распределения случайного числа испытанных приборов, если вероятность выдержать испытание для каждого из них равна 0,9. Найти математическое ожидание числа испытанных приборов. Найти функцию распределения F(x) и построить ее график; найти М(X), (X); построить многоугольник распределения. Вариант 2. Известно, что в партии из 20 телефонных аппаратов 5 недействующих. Случайным образом из этой партии взято 4 аппарата. Построить закон распределения случайной величины Х – числа недействующих аппаратов изотобранных. Найти дисперсию этой случайной величины. В каких единицах она измеряется? Построить график функции распределения F(x) случайной величины Х, многоугольник распределения. Вариант 3. Сырье на завод привозят от трех независимо работающих поставщиков. Вероятность своевременного прибытия сырья от первого поставщика равна 0,4, от второго – 0,7, от третьего – 0,6. Найти математическое ожидание М(X), дисперсию D(X) числа своевременных поставок сырья. Найти функцию распределения и построить ее график. Вариант 4. Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго – 0,3 и от третьего – 0,1. Составить распределение числа прибывших автомашин. Найти математическое ожидание и дисперсию полученной величины. Построить график функции распределения F(x). Вариант 5. Вероятность изготовления бракованной детали р=0,1. Изготовлено 4 детали. Х – случайное число бракованных деталей. Построить закон распределения случайной величины X, найти ее математическое ожидание и дисперсию. Построить график функции распределения, многоугольник распределения. Вариант 6. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, ровно 2. Составить закон распределения случайной величины Х – числа заявок, поступивших за 3 часа. Найти М(X), D(X) и наивероятнейшее число заявок за 3 часа. Вариант 7. В среднем в магазин заходит 3 человека в минуту. Составить закон распределения случайной величины Х – числа зашедших в магазин человек за 2 минуты. Построить многоугольник распределения. Найти М(X), D(X). Вариант 8. Даны законы распределения независимых случайных величин
Составить законы распределения случайных величин: а)XY; б) X+Y. Найти М(X+Y), D(X+Y). Справедливо ли равенство М(X)М(Y)=М(XY)? Вариант 9. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами Х1 и Х2 , которые характеризуются следующими законами распределения:
и Результаты стрельбы одного стрелка не влияют на результат стрельбы другого. Составить закон распределения числа очков, выбиваемых командой, если стрелки сделают по одному выстрелу. Убедиться в справедливости равенства D(Х1+Х2)=D(Х1)+D(Х2). Вариант 10. Производятся выстрелы из орудия с вероятностью попадания в цель 0,9 при каждом выстреле. Стрельба ведётся до первого попадания, но делается не более 4 выстрелов. Составить закон распределения случайной величины X, если: а) X – число произведенных выстрелов; б) X – число промахов; в) X – число попаданий. Найдите математическое ожидание всех найденных случайных величин. Отчет Отчет должен содержать: наименование работы; цель работы; задание; последовательность выполнения работы; ответы на контрольные вопросы; вывод о проделанной работе. Контрольные вопросы 1. Какие значения не может принимать вероятность? 2. Чему равна вероятность достоверного события? Невозможного? 3. Дайте определение закону распределения дискретной случайной величины. 4. Дайте определение математическому ожиданию? Лабораторная работа №5. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

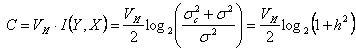 .
.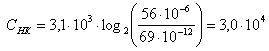 [бит/с].
[бит/с].