МР_к_ЛПЗ_по_ОП.01_09.02.02. Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
|
Практическая работа№2 Тема: Поиск энтропии случайных величин. Цель: научиться вычислять энтропию случайной величины. Время выполнения: 2 часа Оборудование: ПК. Программное обеспечение: операционная система, калькулятор, текстовый редактор. Теоретические основы Энтропия в теории информации — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения. Так, возьмём, например, последовательность символов, составляющих какое-либо предложение на русском языке. Каждый символ появляется с разной частотой, следовательно, неопределённость появления для некоторых символов больше, чем для других. Если же учесть, что некоторые сочетания символов встречаются очень редко, то неопределённость ещё более уменьшается (в этом случае говорят об энтропии n-ого порядка).Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу. Энтропия независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле: 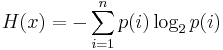 Эта величина также называется средней энтропией сообщения. Величина Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей. Шеннон вывел это определение энтропии из следующих предположений: мера должна быть непрерывной; т. е. изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение энтропии; в случае, когда все варианты (буквы в приведенном примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать полную энтропию; должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых энтропия конечного результата должна будет является суммой энтропий промежуточных результатов. Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме: 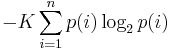 где K — константа (и в действительности нужна только для выбора единиц измерения). Шеннон определил, что измерение энтропии (H = − p1 log2 p1 − … − pn log2 pn), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надежной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидания «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т.д. В общем случае b-арная энтропия (где b равно 2,3,... ) источника = (S,P) с исходным алфавитом S = {a1, …, an} и дискретным распределением вероятности P = {p1, …, pn} где pi является вероятностью ai (pi = p(ai)) определяется формулой: 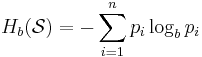 Определение энтропии Шеннона очень связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между понятиями энтропии в термодинамике и теории информации. Например, демон Максвеллатакже противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии. СВОЙСТВА ЭНТРОПИИ 1.Энтропия является вещественной и неотрицательной величиной. 2.Энтропия – величина ограниченная. 3.Энтропия обращается в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно, равны нулю. Это положение соответствует случаю, когда состояние источника полностью определено. 4.Энтропия максимальна, когда все состояния источника равновероятны. 5. Энтропия источника и с двумя состояниями u1 и u2 изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей: р(и1) = р= р(u2) = 1 — р = 0,5. 6.Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропии исходных источников. 7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля. При ее определении используют только вероятности состояний, полностью игнорируя их содержательную сторону. Поэтому энтропия не может служить средством решения любых задач, связанных с неопределенностью. 8. Энтропия как мера неопределенности согласуется с экспериментальными данными, полученными при изучении психологических реакций человека, в частности реакции выбора. Установлено, что время безошибочной реакции на последовательность беспорядочно чередующихся равновероятных раздражителей (например, загорающихся лампочек) растет с увеличением их числа так же, как энтропия. Это время характеризует неопределенность выбора одного раздражителя. Замена равновероятных раздражителей неравновероятными приводит к снижению среднего времени реакции ровно настолько, насколько уменьшается энтропия. Дифференциальной энтропией случайной величины X называется величина: HД(x)=H(x)-H(y)= - 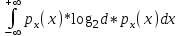 Если произвести квантование случайных величин Х1, Х2…Хn по уровню с числом уровней квантования равным m , то возможное число реализаций длительностью Тn станет конечным и равным М = тn. Каждая из реализаций С1, С2,….Сi,…Сm будет иметь определенную вероятность появления в эксперименте по наблюдению реализаций. Тогда неопределенность (энтропия) и количество информации в реализации (в среднем по всем реализациям) определяются равенством 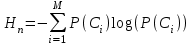 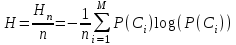 Энтропия и количество информации на одну степеньсвободы (на одну выборку) равны 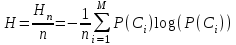 Избыточностьпоказывает, какая доля максимально возможной при заданном объеме алфавита неопределенности не используется источником. 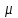 =(Hmax-Hu)/Hmax, =(Hmax-Hu)/Hmax,Где Нu – энтропия рассматриваемого источника, Нmax – максимально возможное значение его энтропии, которое может быть достигнуто подбором распределения и ликвидацией взаимозависимости элементов алфавита. Так, для дискретного источника с М элементами Hmax=logM Выполнение расчетных задач Задача №1 Показать, что для регулярной марковской цепи энтропия H(x)(r) за r шагов равняется энтропии за один шаг, умноженной на число шагов r. Решение: Регулярная цепь Маркова полностью характеризуется матрицей переходных вероятностей 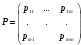 и предельным стационарным распределением вероятностей состояний и предельным стационарным распределением вероятностей состояний 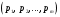 . .В стационарном режиме энтропия за один шаг не зависит от номера шага и равна 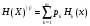 , ,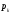 - стационарная вероятность k-го состояния, - стационарная вероятность k-го состояния,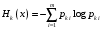 - энтропия в k-м состоянии. - энтропия в k-м состоянии.Энтропия за r шагов равна сумме энтропий за каждый шаг. Так как энтропия за каждый шаг одинакова, то сумма энтропий равна 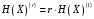 . .Задача №2 В результате полной дезорганизации управления m самолетов летят произвольными курсами. Управление восстановлено, и все самолеты взяли общий курс со среднеквадратической ошибкой отклонения от курса σ=30. Найти изменение энтропии, считая, что в первом случае имело место равномерное распределение вероятностей углов, а во втором случае – нормальное. Решение. Начальное распределение вероятностей углов курсов самолетов равномерное в интервале от 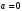 до до 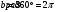 с плотностью вероятности с плотностью вероятности 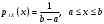 . .Дифференциальная энтропия этого распределения 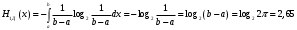 бит. бит.Конечное распределение вероятностей углов курсов самолетов нормальное с параметрами 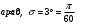 и плотностью вероятности и плотностью вероятности 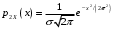 . .Дифференциальная энтропия этого распределения 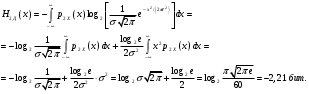 Изменение энтропии 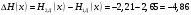 бит. бит.Энтропия уменьшилась на 4,86 бит. Задача №3 Измерительное устройство вырабатывает временные интервалы, распределенные случайным образом в пределах от 100 до 500 мс. Как изменится энтропия случайной величины при изменении точности измерения с 1 мс до 1 мкс? Решение. При точности 1мс дискретная случайная величина Х – результат измерения – может равновероятно принимать одно из 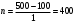 значений. Энтропия равна значений. Энтропия равна 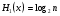 . .При точности 1мкс дискретная случайная величина Х – результат измерения – может равновероятно принимать одно из 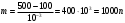 значений. Энтропия равна значений. Энтропия равна 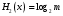 . .Изменение энтропии 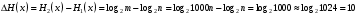 бит. бит.Энтропия увеличилась примерно на 10 бит. Задачи по вычислению энтропии 1. Найдите энтропию для числа белых шаров при извлечении двух шаров из урны, содержащей два белых и один черный шар. 2. Найдите энтропию для числа козырных карт при извлечении двух карт из колоды в 36 карт. 3. Какую степень неопределенности содержит опыт угадывания суммы очков на извлеченной кости из полного набора домино? 4. Найдите энтропию для числа тузов при извлечении трех карт из карт с картинками. 5. Найдите дифференциальную энтропию для равномерного распределения. 6. Найдите дифференциальную энтропию для показательного закона распределения, если известно, что случайная величина хпринимает значение меньше единицы с вероятностью 0,5. Отчет Отчет должен быть оформлен в текстовом редакторе и содержать: наименование работы; цель работы; задание; последовательность выполнения работы; ответы на контрольные вопросы; вывод о проделанной работе. Контрольные вопросы 1. Как определяется энтропия дискретных случайных величин? 2. Приведите примеры энтропий для классических законов распределения. Лабораторная работа №1. Тема: Измерение количества информации. Цель: научиться измерять и вычислять информацию, а также и работать с носителями информации. Время выполнения: 2 часа Оборудование: ПК. Раздаточный материал: дидактический материал Программное обеспечение: операционная система, текстовый редактор. Теоретические основы 1 байт = 8 битов. Существуют еще более крупные единицы измерения информации. Переход к более крупным единицам измерения информации (килобайт, мегабайт, терабайт, петабайт, эксабайт). Байт наиболее удобная единица измерения информационного объема сообщения, состоящего из последовательности символов компьютерного алфавита. Однако она мала при подсчете емкости информационных носителей. По аналогии с физическими единицами измерения (например, 1 килограмм = 1000 грамм) подбираем по таблице целых степеней двойки значение близкое к тысячи. Это значение равно 1024. Поэтому 1 килобайт = 1024 байт = 210 байт, 1 мегабайт = 1024 килобайт = 210 килобайт и т. д. 1 Кбайт (один килобайт) = 1024 байт; 1 Мбайт (один мегабайт) = 1024 Кбайт; 1 Гбайт (один гигабайт) = 1024 Мбайт. Что представляют единицы измерения: 5 бит – буква в клетке кроссворда. 1 байт – символ, введенный с клавиатуры. 6 байт – средний размер слова, в тексте на русском языке. 50 байт – строка текста. 2 Кбайта – страница машинописного текста. 100 Кбайт – фотография в низком разрешении 1 Мбайт – небольшая художественная книга. 100 Мбайт – метровая книга с полками. 1 Гбайт – прочитывает человек за всю жизнь. 3 Гбайт – час качественной видеозаписи. Для сохранения информации используют носители информации: флэш-накопители, флэш-карты, диски разных форматов, съемные жесткие диски. Порядок выполнения работы Изучение материала и выполнение заданий на компьютере. Содержательный (вероятностный) подход к определению количества информации Если заключённые в каком-то сообщении сведения являются для человека новыми, понятными, пополняют его знания, т.е. приводят к уменьшению неопределённости знаний, то сообщение содержит информацию. 1 бит – количество информации, которое содержится в сообщении, которое уменьшает неопределённость знаний в 2 раза. Пример1. При бросании монеты возможны 2 события (случая) – монета упадёт орлом или решкой, причём оба события равновероятны (при большом количестве бросаний количество случаев падения монеты орлом и решкой одинаковы). После получения сообщения о результате падения монеты неопределённость знаний уменьшилась в 2 раза, и, поэтому, количество информации, полученное при этом равно 1 бит. Содержательный (вероятностный) подход является субъективным, т.к. одну и ту же информацию разные люди могут оценивать по разному. Для одного человека сведения в сообщении могут быть важными и понятными, для другого бесполезными, непонятными или вредными. Вычисление количества информации для равновероятных событий. Если события равновероятны, то количество информации можно рассчитать по формуле: N = 2I , где N – число возможных событий, I – количество информации в битах. Задача 1. В коробке 32 карандаша, все карандаши разного цвета. Наугад вытащили красный. Какое количество информации при этом было получено? Задача 2. В школьной библиотеке 16 стеллажей с книгами, на каждом – по 8 полок. Ученику сообщили, что нужный учебник находится на 2-ой полке 4-го стеллажа. Какое количество информации получил ученик? Задача 3. Загадывают число в диапазоне от 1 до 200. Какое наименьшее количество вопросов надо задать, чтобы наверняка отгадать число. На вопросы можно отвечать только «Да» или «Нет». Задача 4. В коробке 50 шаров, из них 40 белых и 10 чёрных. Определить количество информации в сообщении о вытаскивании наугад белого шара и чёрного шара. Задача 5. В озере живут караси и окуни. Подсчитано, что карасей 1500, а окуней - 500. Сколько информации содержится в сообщениях о том, что рыбак поймал карася, окуня, поймал рыбу? Отчет Отчет должен быть оформлен в текстовом редакторе и содержать: наименование работы; цель работы; задание; последовательность выполнения работы; ответы на контрольные вопросы; вывод о проделанной работе. Контрольные вопросы 1. Какое количество информации несет в себе жесткий диск емкостью 4 терабайта, если производитель рассчитывает 1000 за 1024? 2. Чем отличается вероятностный подход к измерению информации от алфавитного? 3. Какие единицы измерения информации используют для флэш-накопителей? Практическая работа №3. Тема: Применение теоремы отчетов. Цель: Изучение возможности синтезирования сигналов по дискретным отсчетам в соответствии с теоремой Котельникова. Время выполнения: 2 часа Оборудование: ПК. Программное обеспечение: операционная система, калькулятор, текстовый редактор. Практическое задание 1. Изобразить сигналы: а) синусоидальный сигнал частотой 5кГц; б) видеоимпульсы прямоугольной формы длительностью 0,25; 0,5; 1,0 мс; в) видеоимпульсы пилообразной формы длительностью 0,5 мс; 1,0 мс. 2. Рассчитать и построить идеальные выборочные сигналы для сигналов, при fвыб=5, 10, 20, 40 кГц. Отчет Отчет должен быть оформлен в текстовом редакторе и содержать: наименование работы; цель работы; задание; последовательность выполнения работы; ответы на контрольные вопросы; вывод о проделанной работе. Контрольные вопросы 1. Сформулируйте теорему Котельникова для сигналов с ограниченным спектром. 2. Объясните погрешности синтезирования реальных сигналов по дискретным отсчетам. Практическая работа №4. Тема: Расчет вероятностей. Цель: Приобрести практические навыки по расчету вероятностей. Время выполнения: 2 часа Оборудование: ПК. Программное обеспечение: операционная система, калькулятор, текстовый редактор. Задачи Задача № 1. Монета подбрасывается три раза подряд. Под исходом опыта будем понимать последовательность (X1, X2, X3), где каждый из Xiобозначает выпадение «герба» (Г) или цифры (Ц). Необходимо: а) Построить пространство W элементарных событий; б) Описать событиеА, состоящее в том, что выпало не менее двух «гербов». Задача № 2. Событие B является частным случаем события A. Чему равны их сумма и произведение? Задача № 3. ПустьА, В, С – случайные события. Выяснить смысл равенств: а) A∩ B ∩ C = A; б) A∪B ∪C = A . Задача № 4. Пусть A, B, C – три произвольных события. Найти выражения для событий, состоящих в том, что из A, B, C: а) Произошло толькоА; б) ПроизошлиАи В, но С не произошло; в) Все три события произошли; г) Произошло по крайней мере одно из этих событий; д) Произошли по крайней мере два события; е) Произошло одно и только одно событие; ж) Произошло два и только два события; з) Ни одно событие не произошло. Задача № 5. В урне имеется 10 шаров: 3 белых и 7 черных. Из урны наугад вынимают один шар. Какова вероятность того, что этот шар: а) белый; б) черный? Задача № 6. Из слова «НАУГАД» наугад выбирается одна буква. Какова вероятность того, что __________эта букваА? Какова вероятность того, что это гласная буква? Задача№ 7. Монета бросается два раза. Найти вероятности событий: 1. А = {герб выпадет один раз}; 2. В = {герб выпадет хотя бы один раз}; 3. С = {герб не выпадет ни разу}. Задача № 8. Бросаются две монеты. Какое из событий является более вероятным: 1. А = {монеты лягут одинаковыми сторонами}; 2. В = {монеты лягут разными сторонами}? Задача № 9. Бросаются одновременно две игральные кости. Найти вероятности событий: 1. А = {произведение выпавших очков равно 8}; 2. В= {сумма выпавших очков равна 8}; 3. С = {произведение выпавших очков четно}; 4. Д = {сумма выпавших очков четна}; 5. Е = {на обеих костях выпадет четное число очков}; Задача № 10. Брошены три монеты. Найти вероятность того, что выпадут два 2 «герба». Задача № 11. При стрельбе была получена относительная частота (частость) попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов? Задача № 12. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно. Задача № 13. Из пяти карточек с буквамиА, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления.Какова вероятность того, что получится слово «ДВА»? Задача № 14. В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два шара окажутся черными? Одного цвета? Разных цветов? Задача № 15. В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными? Задача № 16. Найти вероятность того, что наудачу взятое двузначное число окажется кратным 2, либо 5, либо тому и другому одновременно. Задача № 17. Студент знает 10 вопросов из 30 программы. Определить вероятность того, что из трех предложенных ему преподавателем вопросов студент знает: а) Все три вопроса; б) Хотя бы один вопрос. Задача№ 18. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще только один вопрос? Задача № 19. В круг радиуса R вписан квадрат. Чему равна вероятность того, что поставленные наудачу внутри круга две точки окажутся внутри квадрата? Задача № 20. Среди 25 экзаменационных __________билетов 5 «хороших». Два студента по очереди берут по одному билету. Найти вероятности следующих событий: 1. А ={первый студент взял хороший билет}; 2. В={второй студент взял хороший билет}; 3. С={оба студента взяли хорошие билеты}. Отчет Отчет должен быть оформлен в текстовом редакторе и содержать: наименование работы; цель работы; задание; последовательность выполнения работы; ответы на контрольные вопросы; вывод о проделанной работе. Лабораторные работы № 2-3 Тема: Выполнение расчетов по теореме отчетов. Определение пропускной способности дискретного канала. Цель: научиться выполнять расчеты по теореме отчетов и определять пропускную способность дискретного канала. Время выполнения: 4 часа Оборудование: ПК. Программное обеспечение: операционная система, калькулятор, текстовый редактор. Теоретические основы Пусть на вход аналогово-цифрового преобразователя поступает гармонический сигнал с частотой f(период T= 1/f).частоты исходного сигнала Проведем дискретизацию входного аналогового сигнала с периодом дискретизации Tд меньшим половины периода входного сигнала T (рисунок 1). 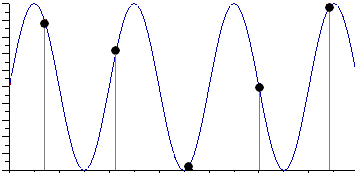 Рисунок 1 Очевидно, что дискретные отсчеты сигнала однозначно не отображают форму исходного сигнала, в частности по получившимся точкам можно построить гармонический сигнал с периодом Tискаж., отличающимся от периода исходного сигнала T. Период Tискаж больше периода исходного сигнала T, соответственно частота меньше, частоты исходного сигнала f (рисунок 2). 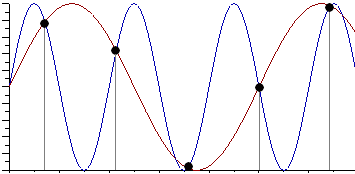 Рисунок 2 Данный эффект называется стробоскопическим эффектом или алиасингом. Он заключается в появлении ложной низкочастотной составляющей при дискретизации сигнала с частотой меньшей удвоенной частоты исходного сигнала (или с периодом большим половины периода исходного сигнала), отсутствующей в исходном сигнале. Пример 2 Уменьшим период дискретизации до половины периода исходного аналогового сигнала (частоту дискретизации увеличим до удвоенной частоты исходного сигнала). В данной ситуации возникает неопределенность начальной фазы и амплитуды сигнала, при этом частота исходного сигнала не искажается. В крайнем случае мы можем получить отсчеты сигнала равные нулю (рисунок 3). 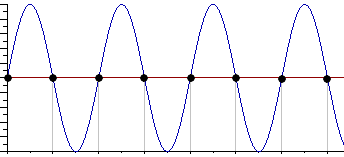 Рисунок 3 Пример 3 Продолжим уменьшение периода дискретизации. Если период дискретизации меньше половины периода исходного сигнала, то очевидно, что через получившиеся после оцифровки точки можно построить только один гармонический сигнал, соотвествующийисходному, без искажения начальной фазы, амплитуды и частоты (рисунок 4). Данное утверждение теоретически обосновано и мы его примем без доказательства. 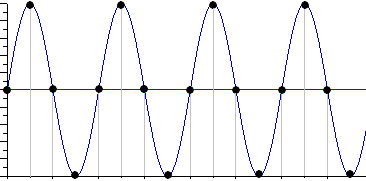 Рисунок 4 Таким образом, для адекватного восстановления гармонического сигнала по дискретным отсчетам, частота дискретизации должна быть не меньше половины частоты сигнала. Частота равная половине частоты дискретизации называется частотой Найквиста fN = fД/2. Данное утверждение можно обобщить следующим образом: Аналоговый сигнал с ограниченным спектром может быть восстановлен однозначно и без искажений по своим дискретным отсчетам, взятым с частотой большей удвоенной максимальной частоты в своем спектре. fд>2·Fmax (1) Данное утверждение известно как теорема Котельникова (в западной литературе теорема Найквиста-Шеннона) или теорема отсчетов. В различных источниках в формулировке данной теоремы могут быть различия, основным из которых является знак сравнения в формуле 1: fд ≥2·Fmaxили fд>2·Fmax. Мы придерживаемся формулировки со знаком строго больше, так как при частоте оцифровки равной максимальной частоте в спектре возникают неоднозначности начальной фазы и амплитуды. На практике аналоговый сигнал, как правило, оцифровывают с частотой в несколько раз превышающей удвоенную частоту в спектре сигнала, хотя существуют методики оцифровки сигнала с нарушением теоремы отсчетов. |
