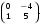Методические указания по выполнению контрольной работы и варианты контрольных работ
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
 ФГБОУ ВО «Уральский государственный экономический университет»  МАТЕМАТИКА Для студентов направления «Управление персоналом» заочной формы обучения 1- 2 семестр Екатеринбург, 2018
В соответствии с учебным планом студенты Центра дистанционного образования в процессе изучения курса «Математика» должны выполнить контрольную работу, которая является важной формой самостоятельной работы студентов. Она способствует углубленному изучению соответствующих тем курса. Ее цель – оказать помощь студентам в изучении математики, проверить усвоение ими отдельных вопросов курса, умение самостоятельно работать с литературой, наличие соответствующих умений и навыков. При подготовке к контрольной работе студенту необходимо научиться работать со справочной и учебной литературой; усвоить основные теоретические положения; уметь анализировать условия задач, выбрать необходимые алгоритм и методы ее решения; оценить и проверить правильность полученного результата. Для повышения эффективности самостоятельной работы студента в ходе выполнения им контрольной работы в данном комплексе приведены пояснения к решению типовых заданий и необходимые теоретические сведения, расположенные в разделе методических указаний по самостоятельной работе студентов в соответствии с темами курса. При оформлении контрольной работы студенту необходимо соблюдать следующие требования:
Контрольная работа выполняется в соответствии с предлагаемыми ниже вариантами. По номеру варианта необходимо выбрать порядковый номер примера в каждом задании каждой темы контрольной работы. Например, для 5 варианта необходимо решить все пятые примеры всех заданий из всех тем контрольной работы. Выбор варианта производится по начальной букве фамилии студента:
Выполненные контрольные работы сдаются на проверку и рецензирование в университет в сроки, установленные учебным планом и графиком изучения дисциплины. При проверке контрольной работы учитываются понимание сути вопроса, знание фактического материала, умение логично и ясно изложить решение. По качеству выполнения работы преподаватель судит об усвоении студентом изучаемых тем, делает замечания и пожелания по процессу изучения дисциплины. Контрольная работа оценивается по принципу «зачтено / не зачтено» и может быть зачтена при условии, что она выполнена с соблюдением распределения вариантов, написана самостоятельно, в соответствии с изученным теоретическим материалом. Проверенная работа может быть возвращена на доработку. В этом случае студент должен провести работу над ошибками в этой же тетради и вновь сдать ее на проверку, указав на обложке, что она сдается повторно. Если рецензент предлагает переделать работу, то необходимо приложить к новой еще и незачтенную работу. Получив зачет по контрольной работе, студент допускается к сдаче экзамена.
Методические указания по выполнению контрольной работы и варианты контрольных работ 1 Варианты контрольных работ 2 Контрольная работа 1(1 семестр) 3 Тема 1. Матрицы и определители 3 Тема 2. Системы линейных уравнений 8 Тема 3. Векторная алгебра. Уравнение прямой 10 Тема 4. Уравнение плоскости 10 Тема 5. Пределы функций 11 Тема 6. Основы дифференцирования 12 Тема 7. Исследование функций 13 Контрольная работа 2 (2 семестр) 14 Тема 8. Неопределенный интеграл 14 Тема 9. Определенный интеграл 16 Тема 10. Несобственный интеграл 17 Тема 11. Ряды 18 Тема 12. Функции нескольких переменных 20 Тема 13. Решение дифференциальных уравнений 20 Тесты для самостоятельного контроля знаний 22 Варианты контрольных работ 4 Контрольная работа 1(1 семестр) 5 Контрольная работа 2 (2 семестр) 12 Тесты для самостоятельного контроля знаний 18
1.1. Вычислить определитель.
1.2. Найти обратную матрицу для матрицы А и сделать проверку.
1.3. Найти 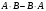
Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса и методом Крамера.
По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж. 1. А(1; 2); В (–1; 2); С(3; 0). 2. А(3; 3); В(–3; –3); С(3; 5). 3. А(–1; 1); В(5; 1); С(3; 7). 4. А(3; 1); В (3; –5); С(–1; –1). 5. А(0; 5); В(5; 0); С(9; 3). 6. А(0; 0); В (8; 2); С(–2; 6). 7. А(–1; 4) В(–1; 2); С(–7; 3). 8. А(2; –1); В(5; 3); С(5; –2). 9. А(3; –3); В(7; –3); С(5; 5). 10. А(9; 0); В(5; 5); С(0; 3).
Даны точки М1 и М2. Составить уравнение плоскости, проходящей через точку ш1 перпендикулярно вектору 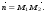 Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость. 1. М1 (–3; 2; 1); М2 (1; 2; 3). 2. М1 (2; –1; 3); М2 (1; 3; 1). 3. М1 (5; –4; 1); М2 (3; 2; 1). 4. М1 (–2; 3; 1); М2 (1; 1; 4). 5. М1 (–1; 4; 3); М2 (2; 5; 1). 6. М1 (2; –1; 5); М2 (–2; 1; 3). 7. М1 (3; 2; –2); М2 (5; 1; 2). 8. М1 (2; –5; 4); М2 (1; 3; 4). 9. М1 (2; 2; –1); М2 (1; 3; 1). 10. М1 (4; –2; 1); М2 (3; 1; 2).
Вычислить пределы. 1. а) 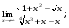 б) б) 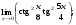 в) в) 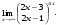 2. а) 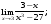 б) б) 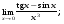 в) в) 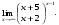 3. а) 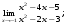 б) б) 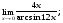 в) в) 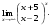 4. а) 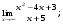 б) б)  в) в) 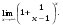 5. а) 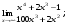 б) б) 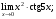 в) в) 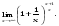 6. а) 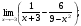 б) б) 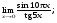 в) в) 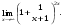 7. а) 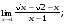 б) б)  в) в) 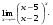 8. а) 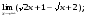 б) б) 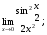 в) в) 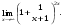 9. а) 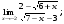 б) б) 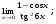 в) в) 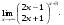 10. а) 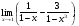 б) б) 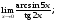 в) в) 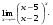
Найти производную сложной функции.
Исследовать функцию и построить ее график.
Вычислить неопределенный интеграл. 1. а) 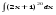 ; б) ; б) 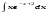 ; в) ; в) 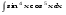 ; ; г) 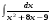 . .2. а) 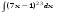 ; б) ; б)  ; в) ; в) 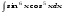 ; г) ; г)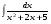 . .3. а) 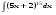 ; б) ; б) 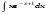 ; в) ; в) 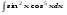 ; ; г) 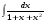 . .4. а) 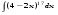 ; б) ; б) 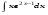 ; в) ; в) 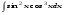 ; ; г) 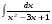 . . 5. а) 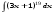 ; б) ; б) 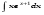 ; в) ; в) 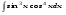 ; ; г) 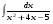 . .6. а)  ; б) ; б) 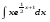 ; в) ; в) 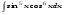 ; г) ; г)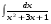 . . 7. а) 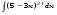 ; б) ; б) 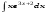 ; в) ; в) 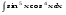 ; ; г) 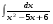 . .8. а) 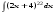 ; б) ; б) 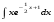 ; в) ; в) 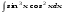 ; ; г) 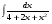 . .9. а) 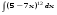 ; б) ; б)  ; в) ; в) 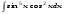 ; ; г) 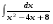 . .10. а) 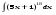 ; б) ; б) 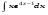 ; в) ; в) 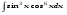 ; ; г) 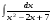 . .
9.1. Вычислить определенный интеграл. 1. а) 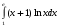 ; б) ; б) 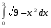 . .2. а) 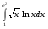 ; б) ; б) 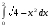 . .3. а) 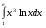 ; б) ; б)  . .4. а) 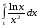 ; б) ; б) 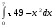 . .5. а) 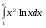 ; б) ; б) 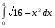 . .6. а) 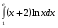 ; б) ; б) 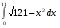 . .7. а) 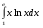 ; б) ; б)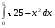 . .8. а)  ; б) ; б) 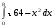 . . 9. а) 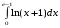 ; б) ; б) 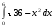 . .10. а) 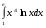 ; б) ; б) 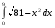 . .9.2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж. 1.  2. 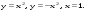 3. 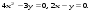 4. 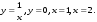 5. 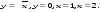 6. 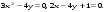 7.  8.  9.  10. 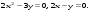
Вычислить интеграл или установить его расходимость. 1. а) 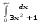 ; б) ; б) 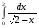 . .2. а) 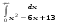 ; б) ; б) 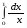 . .3. а) 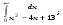 б) б)  4. а) 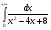 ; б) ; б) 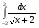 . .5. а) 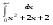 ; б) ; б) 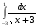 . .6. а) 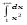 ; б) ; б) 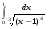 . .7. а) 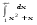 ; б) ; б) 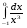 . .8. а) 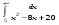 ; б) ; б) 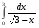 . .9. а) 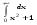 ; б) ; б)  . .10. а) 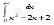 ; б) ; б) 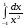 . .
11.1. Числовые ряды. Исследовать ряд на сходимость.
11.2. Степенные ряды. Определить область сходимости степенного ряда.
Исследовать функцию на экстремум.
13.1. Найти общее и частное решения дифференциального уравнения. 1. 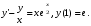 2. 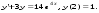 3. 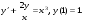 4. 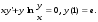 5.  6. 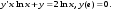 7. 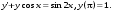 8.  9. 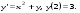 10. 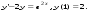 13.2. Найти общее решение дифференциального уравнения.
1. Разложение по первой строке определителя 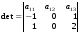 имеет вид: имеет вид:
2. Даны матрицы 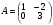 и и 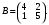 Тогда А – B равно: Тогда А – B равно:
3. Матрица 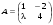 не имеет обратной при λ, равном: не имеет обратной при λ, равном:а) –1; б) 0; в) –2; г) 1. 4. Система линейных уравнений с основной матрицей 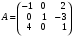 и вектором правых частей и вектором правых частей 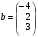 имеет вид: имеет вид:а) 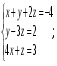 б) б) 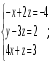 в)  г) г) 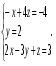 5. Длина отрезка, отсекаемого прямой 2x + 4y – 8 = 0 на оси Ox, равна: а) 3; б) 5; в) 4; г) 8. 6. Найдите уравнение прямой, перпендикулярной прямой y = –4x + 1: а) 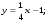 б) б) 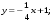 в) в) 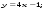 г) г) 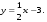 7. Координата x0 точки A(x0, 5, 10) принадлежащей плоскости 2x – y + z – 10 = 0, равна: а) –2; б) 0; в) 2,5; г) 1. 8. Значение предела 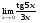 равно: равно:а) 0; б) 5/3; в) 1; г) 3/5. 9. Закон движения материальной точки имеет вид x(t) = t3 – 4t, где x(t) – координата точки в момент времени t. Тогда скорость точки при t = 2 равна … а) 24; б) 8; в) 18; г) 20. 10. На рисунке изображен график производной функции y = f(x), заданной на отрезке [–1; 8]. 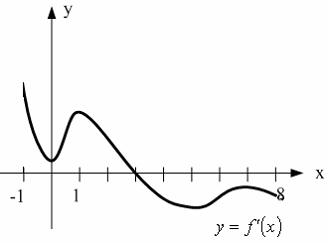 Тогда точкой максимума этой функции является: а) 8; б) 0; в) 3; г) –1. 11. Множество первообразных функции f(x) = sin3x имеет вид: а) 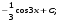 б) б) 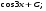 в) 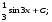 г) г) 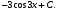 12. Вектор 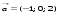 перпендикулярен вектору перпендикулярен вектору 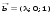 , если λ равно: , если λ равно:а) 1; б) –2; в) –1; г) 2. 13. Векторы 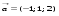 и и 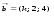 коллинеарны, если k равно: коллинеарны, если k равно:а) 1; б) –2; в) –10; г) 4. 14. Если 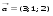 и и 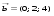 , тогда скалярное произведение , тогда скалярное произведение  равно: равно:a) 5; б) 10; в) 7; г) 12. 15. Модуль комплексного числа 1 + i равен: a) 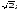 б) 4; в) 7; г) 3. б) 4; в) 7; г) 3.16. Если z = 5 – 2i, то сопряженное ему комплексное число 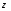 равно: равно:a) 5 + 2i; б) –5 – 2i; в) 5i – 2; г) –5+2i. 17. Действительная часть комплексного числа (1 – i)2 равна: a) 2; б) –1; в) 0; г) 1. 18. Значение функции f(z) = 3z – 1 в точке z0 = 1 + 2i равно: a) –2 + 6i; б) 2 + 6i; в) –1 + 4i; г) –2 + 5i. 19. Периодической является функция: a) f(x) = x + x2; б) f(x) = sin(x + π); в) f(x) = lnx; г) f(x) = 5π. 20. Для периодической функции f(x) с периодом T = 3, при всех x из области определения, выполняется равенство: a) f(x + 3) = f(x); б) f(x – 3) = f(x); в) f(3x) = f(x); г) f(x/3) = f(x). 21. Если 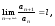 то числовой ряд сходится при l, равном: то числовой ряд сходится при l, равном:a) 0,5; б) 1; в) –2; г) 2. 22. Общий интеграл дифференциального уравнения 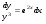 имеет вид: имеет вид:a) 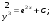 б) б) 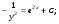 в) 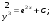 г) г) 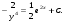 23. Дано дифференциальное уравнение 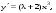 тогда функция y = x4 является его решением при λ, равном: тогда функция y = x4 является его решением при λ, равном:a) 2; б) 1; в) 3; г) 0. 24. Дано дифференциальное уравнение 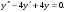 Тогда соответствующее ему характеристическое уравнение имеет вид: Тогда соответствующее ему характеристическое уравнение имеет вид:a) 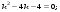 б) б) 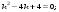 в)  г) г) 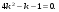 25. Частная производная по y функции  равна: равна:a)  б) б) 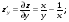 в) 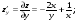 г) г) 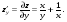 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

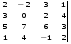
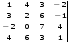 1.
1. 
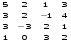 3.
3. 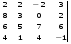
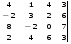 5.
5. 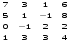
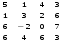 7.
7. 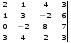
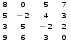 9.
9. 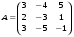
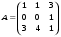 1.
1. 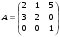
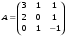 3.
3. 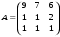
 5.
5. 
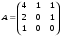 7.
7. 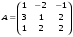
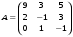 9.
9. 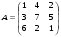
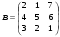
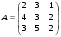
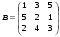 1.
1. 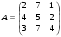
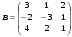

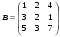 3.
3. 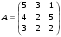


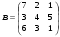 5.
5. 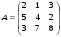
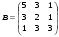
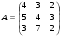
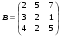 7.
7. 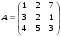
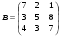
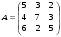
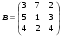 9.
9. 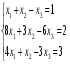
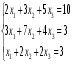 1.
1. 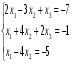
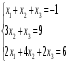 3.
3. 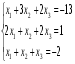
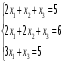 5.
5. 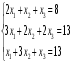
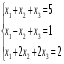 7.
7. 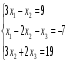
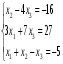 9.
9. 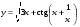
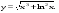 1.
1. 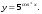
 3.
3. 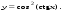
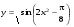 5.
5. 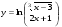
 7.
7. 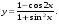
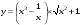 9.
9. 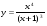
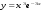 1.
1. 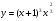
 3.
3. 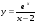
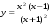 5.
5. 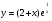
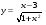 7.
7. 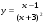
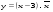 9.
9. 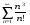
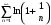 1.
1. 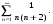
 3.
3. 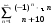
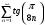 5.
5. 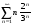
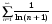 7.
7. 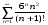
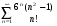 9.
9. 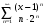
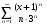 1.
1. 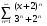
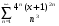 3.
3. 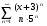
 5.
5. 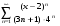
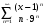 7.
7. 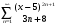
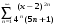 9.
9. 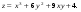
 1.
1. 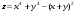
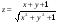 3.
3. 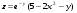
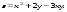 5.
5. 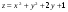
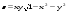 7.
7. 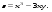
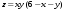 9.
9. 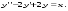
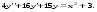 1.
1. 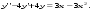
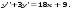 3.
3. 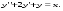
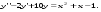 5.
5. 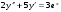
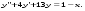 7.
7. 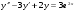
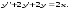 9.
9. 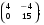 б)
б) 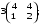 в)
в) 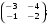 г)
г)