Методические указания по выполнению курсового проекта по дисциплине
 Скачать 1.31 Mb.
|
|
7. КОНИЧЕСКАЯ ЗУБЧАТАЯ ПЕРЕДАЧА 7.1. Общие сведения. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом . Наиболее распространены передачи с углом = 900. Конические зубчатые колеса могут быть выполнены с прямыми, косыми и криволинейными зубьями. Колеса с косыми и криволинейными зубьями отличаются более плавной и бесшумной работой и допускают большие окружные скорости, чем колеса с прямыми зубьями. Конические зубчатые колеса с прямыми зубьями рекомендуется применять при окружных скоростях, не превышающих 2 м/с. Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и специальные инструменты. 7.2. Последовательность проектного расчета 1. Выбираем тип конических колес (прямозубые, косозубые, с криволинейными зубьями). 2. Выбираем материал для шестерни и зубчатого колеса (учитывая, что редуктор должен иметь сравнительно небольшие габариты и невысокую стоимость, см. раздел 4.1.). По табл. 4.1. назначаем для колес термообработку и определяем механические свойства материалов ( T , B). 3. Определяем допускаемые напряжения (допускаемые контактные напряжения [н], допускаемые напряжения изгиба [O]F, или [-1]F, допускаемые напряжения при кратковременной нагрузке []Hmax и []Fmax (см. раздел 5.2. формулы: 5.6; 5.11; 5.16; 5.17). 4. Определяем вращающийся момент по валу шестерни  .Вращающий момент на валу колеса Т2 = Т1 u ( Н мм) где u - передаточное число, принятое для данной передачи. 5. Определяем внешний делительный диаметр колеса а) прямозубые колеса 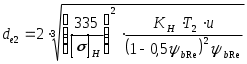 ; (7.1.)б) колеса с косыми и кривыми зубьями  . (7.2.)Результат округлить по СТ СЭВ 229-75 (см.раздел 6.2., пункт 6). Здесь коэффициент ширины зубчатого венца  (Re - внешнее конусное расстояние).При проектировании редукторов рекомендуется принимать вRe=0,285. Коэффициент нагрузки Kн принимают предварительно для колес с твердостью поверхностей зубьев < HB350 Kн=1,2, при твердости >HB350 Kн=1,35. При проверочном расчете значения Kн уточняются. 6. Определяем число зубьев колес. Для шестерни Zmin=17cos 1 ·cos . Рекомендуем выбирать Z1=18 ... 30. Число зубьев колеса Z2=Z1· u. 7. Так как найденные значения Z1 и Z2 округляются до целых чисел, то после этого следует уточнить  . Расхождение с принятым ранее номинальным не должно превышать 3%.8. Определяем внешний окружной модуль  (7.3.)(округлять me до стандартного значения для конических колес не обязательно). 9. Уточняем значение. de2 = me ·Z2; отклонение от стандартного не должно превышать 3%. 10. Определяем углы делительных конусов ctg 1 = u , 1 = arcctg u , 2 = 900 - 1 ; 11. Определяем внешнее конусное расстояние Re и ширны венца b:  ; (7.4.)12. Определяем внешний делительный диаметр шестерни  (7.5.)13. Определяем средний делительный диаметр шестерни  (7.6.)14. Определяем внешние диаметры верхних зубьев шестерен и колеса:  (7.7.)15. Определяем средний окружной и средний нормальный модули зубьев:  (7.8.) (7.9.)=15...300 - для косозубых колес; =30...400 - для кривых колес; = 00 - для шевронных колес. 16. Определяем внешнюю высоту зуба: а) для прямозубых колес  (7.10.)б) для колес с круговыми и косыми зубьями  (7.11.)17. Определяем внешнюю высоту головки зуба: а) для прямозубых колес  б) для колес с круговыми и косыми зубьями  (7.12.) (7.13.)где Х1 - коэффициент радиального смещения шестерни:  (7.14.)18. Определяем внешнюю высоту ножки а) для прямозубых колес  (7.15.)б) для колес с круговыми и косыми зубьями  ;  (7.16.)19. Определяем коэффициент ширины шестерни по среднему диаметру  (7.17.)20. Определяем среднюю окружную скорость и степень точности колес  Для редукторных конических зубчатых передач надо, как правило, назначать 7-ю степень точности изготовления, значения коэффициентов брать такие, которые соответствуют 8-й степени точности цилиндрических зубчатых колес. 21. Для проверки контактных напряжений уточняем значение коэффициента нагрузки Kн: КH = KН · KН · KHV. Значение KН берется из таблицы 6.2. Значение KН - из таблицы 6.3. Значение KHV - из таблицы 6.4. 22. Проверяем выносливость различных рабочих поверхностей зубьев по контактным напряжениям: а) для прямозубых колес 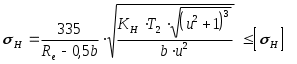 (7.18.)б) для колес с косыми и кривыми зубьями:  (7.19.)23. Определяем силы, действующие в зацеплении: а) для прямозубых колес окружная сила  ;радиальная для шестерни, равная осевой для колеса  (7.20.)осевая для шестерни, равная радиальной для колеса  (7.21.)б) для колес с круговыми и косыми зубьями окружная сила ;радиальная сила  ; (7.22.)осевая сила  . (7.23.)В последних формулах знак зависит от направления внешнего момента, приложенного к валу шестерни и линии наклона зуба как винтовой линии (табл.7.1.). Таблица 7.1.
Примечание: Направление Т1 определяется при наблюдении со стороны большого торца шестерни. 24. Проводим проверку зубьев на выносливость по напряжениям изгиба: а) для прямозубых колес  (7.24.)Расчет следует вести для зубьев того из колес, для которого отношение  меньше. При одинаковых материалах и их механических характеристиках YF больше для шестерни, поэтому именно для зубьев шестерни и ведут расчет.Значение коэффициента прочности зубьев по местным напряжениям даны в ГОСТе 21354-75 в виде графиков с учетом коэффициента смещения. Для зубчатых колес, выполненных без смещения, YF имеет следующие значения: Z .... 17 20 25 30 40 50 60 80 100 и более YF .... 4,28 4,09 3,90 3,80 3,70 3,66 3,62 3,61 2,60 Для конических прямозубых колес значение коэффициента YF выбирают в зависимости от эквивалентных чисел зубьев Zv: для шестерни  ;для колеса  .Коэффициент нагрузки KF представляет собой произведение двух коэффициентов: КF = KF · KFV. Значение коэффициента KF и KFV даны в табл. 6.5. и 6.6. Для колес с круговыми и косыми зубьями:  . (7.25.)Здесь коэффициент YF имеет то же значение, что и в формуле (7.24.), с той, однако, разницей, что его следует выбирать по биэквивалентному числу зубьев Zv :  (7.26.)Коэффициент Y учитывает повышение прочности криволинейных зубьев по сравнению с прямолинейными:  (7.27.)где - угол наклона делительной линии зуба, в градусах. Коэффициент KF учитывает распределение нагрузки между зубьями:  (7.28.)где - коэффициент торцевого перекрытия; n - степень точности колес. При учебном проектирование можно принимать среднее значение =1,29 и степень точности 7-ю, тогда KFa = 0,885. 25. Проводим проверку прочности зубьев при перегрузках: а) по контактным напряжениям  ;б) по напряжениям изгиба  .8. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ 8.1. Общие сведения Червячные передачи относятся к категории зубчато-винтовых передач. Их применяют в случаях, когда геометрические оси ведущего и ведомого валов перекрещиваются. Угол перекрещивания обычно равен 900 . Возможны и другие углы, отличные от 900 , однако, такие передачи встречаются редко. Червячные передачи выполняют либо открытыми, либо закрытыми в виде отдельных агрегатов - червячных редукторов. В силовых червячных передачах число витков червяка выбирают в пределах Z1=1...4, а число зубьев червячного колеса Z2=27...70 (при небольших нагрузках в отдельных случаях до 120). Таким образом, посредством одноступенчатой силовой червячной передачи можно получить и (передаточное число) примерно от 7 до 70 и в некоторых случаях 120. Применение червячных редукторов при малых передаточных числах (u < 10) нецелесообразно. По ГОСТу 2144-66 (передачи червячные и цилиндрические) предусмотрено два ряда передаточных чисел в пределах 8...80, осуществляемых при числе заходов червяка равном 1 или 2, или 4 (трехзаходные червяки в ГОСТ не включаются) и число зубьев колеса Z2=30...80. Значения промежуточных чисел по указанному ГОСТу следующее: 1-й ряд ... 8; 10; 12,5; 16; 20; 25; 31,5; 40; 50; 63; 80; 2-й ряд ... 9; 11,2; 14; 18; 22,4; 28; 35,5; 45; 56; 71. Первый ряд следует предпочитать второму. Фактические передаточные числа uф не должны отличаться от указанных номинальных более чем на 5%. При проектировании червячной передачи (редуктора) с нестандартными параметрами (кроме m и q) для выбора Z1 и Z2 при заданном передаточном числе можно пользоваться таблицей 8.1. 7.2. Последовательность проектного расчета 1. Исходя из требований компактности и передаточного числа, выбираем число зубьев червячного колеса: Z2 = u ·Z1 (8.1.) 2. В зависимости от условий работы передачи (учитывается, что редуктор должен иметь сравнительно небольшие габариты и невысокую стоимость) назначаем материал червяка и венца червячного колеса (см. раздел 4.2.). Таблица 8.1- Рекомендуемые значения Z1 и Z2 для нестандартных червячных передач
3. Определяем основные допускаемые контактные напряжения []'н и напряжения изгиба [0]'F или [-1]'F для выбранных материалов по таблице 5.3. Расчетные значения допускаемых напряжений при длительной работе получаем умножением табличных значений основных напряжений на коэффициент долговечности (см. раздел 5.4, червячные передачи). Допускаемые контактные напряжения могут также выбираться из табл. 5.4 (в случаях, указанных в разделе 5.2), предварительно приняв скорость скольжения Vc= 2,5...4 м/с. Определяем также предельные допускаемые напряжения по табл. 5.5. 4. Принимаем предварительно коэффициент диаметра червяка (q=8...12) и коэффициент нагрузки ( K=1,05...1,4 ), большие значения для окружных скоростей колеса Vc > 3м/с и ударных нагрузок. 5. Определяем вращающий момент на валу колеса.  (8.2.)6. Определяем межосевое расстояние из условия контактной прочности  (8.3.)где Eпр - приведенный модуль упругости.  (8.4.)где E1 - модуль упругости материала червяка; E2 - то же венца червячного колеса. Для стали E1 = 2,15·105 H/мм2 ; для чугуна E2 =(0,885...1,18) · 105 H/мм2 ; для бронзы E2 = (0,885...1,13)·105 H/мм2 (большие для твердых безоловянных бронз). Формула (8.3) и приведенная ниже формула (8.20) соответствует наиболее распространенной форме венца червячного колеса, при которой условный угол обхвата 2 =1000. При ином значении, числовые коэффициенты в указанных формулах следует умножить на коэффициент  (8.5.)7. Определяем расчетный модуль зацепления  . (8.6.)Полученное значение модуля округляем до ближайшего стандартного значения (см. табл. 8.2.). Округление модуля повлечет за собой изменение межосевого расстояния и может оказаться, что предварительно принятое значение q не соответствует найденному модулю. После выбора стандартных значений m и q, необходимо вычислить фактическое межосевое расстояние, соответствующее принятым параметрам:  . (8.7.)8. Определяем основные размеры червяка: а) делительный диаметр червяка d1 = q · m ; (8.8.) б) диаметры вершин витков червяка da1 = d1 + 2m; (8.9.) в) диаметры впадин витков червяка df1 = d1 - 2,4m; (8.10.) г) длину нарезанной части червяка при Z1= 1 или 2 b1 > (11 + 0,06 Z2) m1 Z2 = 3 или 4 b1 > (12,5 + 0,09 Z2) m1 (8.11.) Для шлифуемых и фрезеруемых червяков величина b1, полученная по указанным соотношениям, должна быть увеличена при m <10мм на 25 мм, при m =10...16мм на 35... 40мм и при m > 10 мм на 50мм; д) делительный угол подъема витка червяка  (8.12.)(угол определяется с точностью до секунды). 9. Определяем основные размеры червячного колеса: а) делительный диаметр червячного колеса d2 = Z2· m ; б) диаметры вершин зубьев червячного колеса da2 = d2 + 2m; в) диаметры впадин зубьев червячного колеса df2 = d2 - 2,4m; г) наибольший диаметр червячного колеса  (8.13.)Таблица 8.2- Сочетание модулей m и коэффициентов диаметра червяка q (по ГОСТу 2144-66)
д) ширина венца червячного колеса при Z1= 1...3 , b1 < 0,75 da1 Z2 = 4 , b1 < 0,67 da1 (8.14.) 10. Определяем окружную скорость червяка  (8.15.)11. Определяем скорость скольжения  (8.16.)12. Уточняем коэффициент полезного действия червячной передачи с учетом потерь в зацеплении, в опорах и на разбрызгивание и перемешивание масла:  (8.17.)где - приведенный угол трения. Значения f и рекомендуется принимать в зависимости от скорости скольжения Vc по табл. 8.3. 13. По табл. 8.4. выбираем степень точности передачи и определяем коэффициент динамичности Kv. 14. Определяем коэффициент неравномерности распределения нагрузки  , (8.18.)где - коэффициент деформации червяка, определяемый по табл. 8.5.; - вспомогательный коэффициент, зависящий от характера изменения нагрузки. При постоянной нагрузке = 1,0; при незначительных колебаниях нагрузки = 0,6; при значительных колебаниях нагрузки = 0,3. 15. Определяем коэффициент нагрузки K = K·KV. (8.19.) По СТ СЭВ установлено 12 степеней точности для червячных передач; для силовых передач назначаются степени точностью от 5 до 9-й в порядке убывания точности; для редукторов общего назначения применяют в основном 7 и 8-ю степени точности. Таблица 8.3-Приведенные коэффициенты трения f' и углы трения при работе червячного колеса из оловянной бронзы по стальному червяку
Примечание: 1. Меньшие значения следует принимать при шлифованном или полированном червяке. 2. При венце колеса из безоловянной бронзы или латуни табличные значения следует увеличивать на 30-50%. Таблица 8.4-Коэффициент динамичности нагрузки KV
Таблица 8.5-Коэффициент деформации червяка
16. Проверяем контактное напряжение:  (8.20.)Результат проверочного расчета следует признать неудовлетворительным, если н превышает [] н более чем на 5 % (передача перегружена), а также в случае, если расчетное напряжение ниже допускаемого на 15% и более (передача недогружена). 17. Проверка прочности зубьев червячного колеса на изгиб:  (8.21.)где YF - коэффициент формы зуба, определяемый из таблицы 8.6. в зависимости от эквивалентного числа зубьев.  (8.22.)Таблица 8.6 -Коэффициент формы зуба YF для червячных колес
18. Проводим проверку прочности зубьев при перегрузках по контактным напряжениям: а) по контактным напряжениям ;б) по напряжениям изгиба . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||