Бланк для лабораторной работы №3 Атомы. Методические указания по выполнению курсового проекта по дисциплине Электрический привод
 Скачать 1.85 Mb. Скачать 1.85 Mb.
|
|
6.3 Пояснения к п. 11 «Расчёт переходных процессов ( зависимости t, М(t), 0t))» Независимо от типа системы электропривода и способа формирования переходных процессов общий порядок их расчёта одинаков: На построенных статических механических характеристиках двигателя и РМ находят характерные точки, определяют начальные и конечные условия переходного процесса. Рассчитывают переходные процессы, т.е. зависимости t, М(t),0t. Строят графики этих зависимостей. При расчётах необходимо иметь в виду, что двигатель в переходном режиме должен быть полностью использован по моменту. Вместе с тем нагрузка не должна превышать допустимую. Если скорость двигателя постоянного тока регулируется изменением магнитного потока, необходимо учитывать электромагнитные переходные процессы в обмотке возбуждения. При свободном выбеге расчёт переходного процесса сводится к расчёту времени выбега. Отличительным для свободного выбега является равенство нулю момента двигателя и совпадение с осью скоростей его механической характеристики, а динамический момент равен статическому, взятому с обратным знаком. Время свободного выбега: где – скорость, при которой двигатель отключается от источника питания; МС – соответствующий этой скорости статический момент. При линейных механических характеристиках двигателя и одинаковых их жесткостях во всем диапазоне скоростей вращения и линейных механических характеристиках РМ возможен аналитический метод расчёта переходных процессов при питании двигателя от вентильного преобразователя в системах ТП–Д и ПЧ–АД. Для расчёта переходных процессов в случае, когда предполагается ослаблять магнитный поток двигателя в системе ТП–Д с целью обеспечения работы ЭП на регулировочной характеристике, расположенной выше основной (см. рис. 8), необходимо выполнить следующее [21, с. 431]: По универсальной кривой намагничивания, приведенной в приложении, а также в [4, с. 34], рассчитывается и строится кривая намагничивания двигателя Ф(IB). Рассчитывается начальное ФНАЧ и конечное ФКОН значения потока. В качестве ФНАЧпринимается номинальный поток,ФН двигателя, работающего на основной характеристике (М). Методика определения требуемого ФКОН изложена в п. 9 настоящих указаний (определение По кривой намагничивания Ф(IB) определяется начальное IВ.НАЧ и конечное IВ.КОН значения токов возбуждения двигателя. По конечному значению IВ.КОН рассчитывается добавочное сопротивление, которое необходимо включить в цепь ОВД для получения требуемого магнитного потока Рассчитывается электромагнитная постоянная ТВ контура возбуждения Рассчитывается и строится кривая IВ(t): Длительность переходного процесса Используя кривые Ф(IB) и IB(t), строится кривая Ф(t). Строится кривая (t), где – магнитный поток в относительных единицах: Кривая разбивается на На каждом i-м интервале определяется среднее значение ср.i относительного потока. Рассчитывается приращение скорости вращения ЭП на каждом i-м интервале: 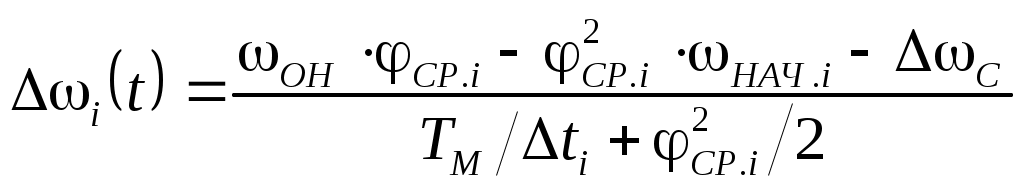 , ,где Одновременно строится кривая скорости (t), т.к. Рассчитывается кривая I(t), по уравнению: Рекомендации относительно численного значения величины U изложены в п. 9 настоящих указаний. Рассчитывается зависимость М(t): Рассчитывается зависимость Строятся графики переходных процессов (рис. 3). 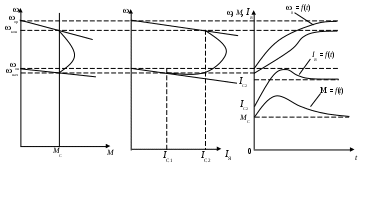 Рисунок 3. Статические характеристики, динамическая характеристика и графики переходных процессов при ослаблении магнитного потока двигателя Примечание: Методика расчёта переходных процессов при усилении магнитного потока двигателя с целью перевода режима работы ЭП с регулировочной характеристики на основную (рис. 4) идентична выше изложенной. В этом случае при определении величины ТВ положить RД = 0.                        , M, IЯ    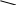 0 = f(t) а a  = f(t)    б б IЯ = f(t) M = f(t) Мс М IС1 IC2 I t Рисунок 4. Статические характеристики, динамическая характеристика и графики переходных процессов при усилении магнитного потока двигателя Расчёт переходных процессов в системах ТП–Д и ПЧ–АД [1, с. 302; 2, с. 225; 21, с. 401] Расчёт переходных процессов в разомкнутой системе электропривода при питании двигателя от вентильного преобразователя предлагается выполнить в предположении, что управление приводом осуществляется путем линейного изменения во времени скорости идеального холостого хода (скорости вращения магнитного поля (синхронной скорости) у асинхронных двигателей), т.е. по закону: где 0 – ускорение скорости идеального холостого хода, определяемое из условия полного использования двигателя по моменту. Так как скорость нарастания управляющего сигнала ограничивается, электромагнитная инерция силовой цепи двигателя в переходном процессе проявляется незначительно и ею можно пренебречь. Ниже излагается сущность аналитического расчёта при линейном изменении скорости идеального холостого хода 0(t) для случая При определении длительности изменения 0 необходимо учитывать знак ускорения 0 > 0 при пуске в области положительных скоростей и при торможении в области отрицательных скоростей. Ускорение 0 < 0 при пуске в области отрицательных скоростей и при торможении в области положительных скоростей. Следует иметь в виду, что суммарная длительность переходных процессов (пуск, изменение скорости, торможение) не должно превышать (23)% от времени цикла. Скорость двигателя и его момент в переходных режимах при питании от вентильного преобразователя изменяются по законам: 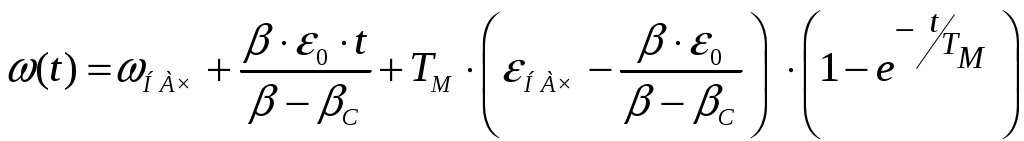 (1) (1)Эти выражения получены для самых общих условий протекания переходных процессов, имеют общий характер и могут использоваться для расчёта этих процессов. В этих выражениях и С – соответственно коэффициенты жесткости механических характеристик двигателя и РМ. где Примечание. При определении βс значения момента и скорости берутся для точек расположенных в одном квадранте (если точки расположены в разных квадрантах, то отрицательные значения берутся по модулю). Ускорение идеального холостого хода 0 рассчитывается, как уже сказано выше, из условия полного использования двигателя по моменту в переходных процессах: где ММ,МС.М – соответственно максимально допустимый момент двигателя и максимальный статический момент; Для ДПТ Тм – электромеханическая постоянная времени электропривода, нач – начальное угловое ускорение электропривода, Для расчёта начального момента сопротивления используют формулу где МСМ – закон изменения момента сопротивления (см. табл. 2). Расчёт переходных процессов рекомендуется вести в такой последовательности: А). Разгон системы из неподвижного состояния (рис. 5). В этом случае переходный процесс разбивается на три этапа. На I-м этапе, 0 ≤ t ≤ t0, ротор (якорь) остается неподвижным, поскольку момент двигателя меньше момента сопротивления. Начальная механическая характеристика двигателя проходит через начало координат, конечная – через точку с координатами = 0 и М = МС0 (ей соответствует 0 = 0.кон.I). 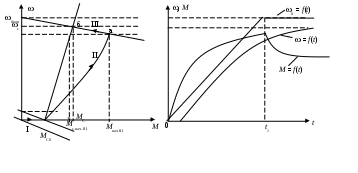 нач.III 0кон.I Рисунок 5. Статические и динамическая характеристики, и графики переходных процессов при пуске ЭП Для данного этапа справедливы начальные условия: Примечание: При расчёте переходных процессов необходимо учитывать, что ε0 положительна в четвертом и первом квадрантах и отрицательна во втором и третьем. будет положительная и равна епсилон0 торможения. Момент двигателя на этом этапе изменяется по закону Заканчивается I-й этап при увеличении М до МС0, когда скорость 0 достигает значения: Длительность этапа: На II-м этапе начало отсчета переносят в t0. За время t0 ≤ t ≤ t1 (см. рис. 5) происходит разгон двигателя при линейном изменении 0 во времени. Начальные условия этого этапа: Скорость и момент на данном этапе описываются уравнениями : 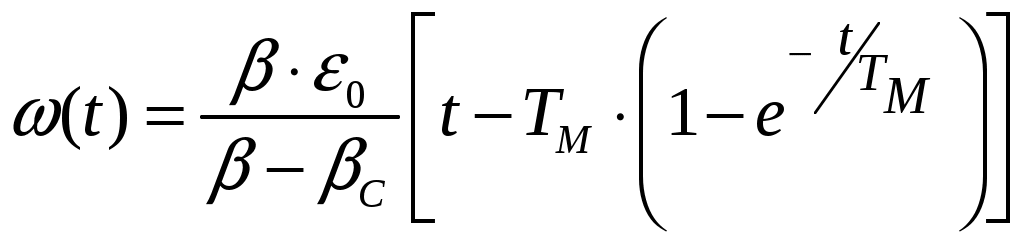 , (3) , (3)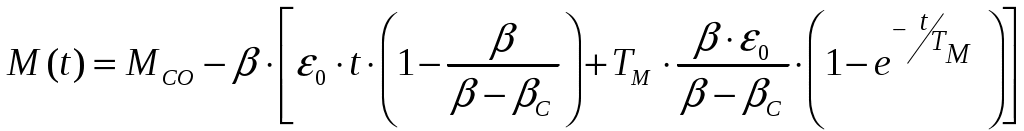 . (4) . (4)Величина 0 имеет то же значение, что и на первом этапе. Начальная механическая характеристика двигателя на II-м этапе совпадает с конечной характеристикой I-го этапа, конечная характеристика II-го этапа проходит через точку «а» заданного установившегося режима работы. Заканчивается этап в момент времени t1, когда двигатель выходит в точку «а» на характеристику, обеспечивающую заданную скорость РМ, при этом ω0 достигает значения ω0. кон (см. рис. 5). Длительность II-го этапа: На III-м этапе t > t1 (см. рис. 5) происходит окончательный разгон двигателя до установившегося режима при постоянном значении скорости идеального холостого хода ω0. кон. Для этого этапа начальные условия: Уравнение скорости на этапе имеет вид: 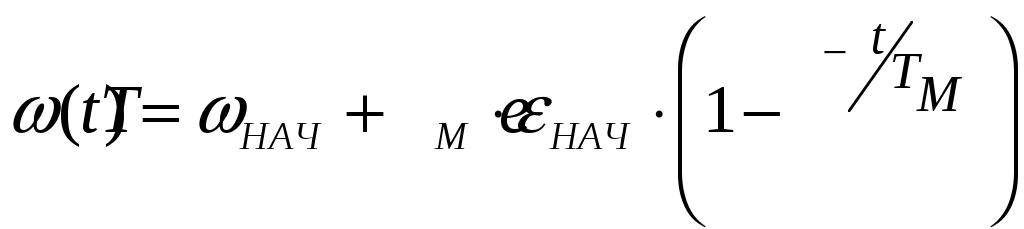 . (5) . (5)Данное уравнение можно представить также в виде: Уравнение момента имеет вид: 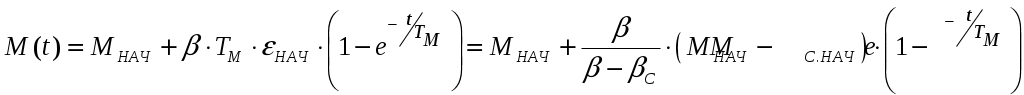 . . После ряда преобразований получаем: Длительность этапа: Б) Увеличение скорости системы (см. рис. 6). Полагаем, что исходный режим работы был установившимся, двигатель работал на начальной характеристике в точке «а». В данном случае переходный процесс разбивается на два этапа: этап разгона при линейном изменении ω0 Начальные условия I-го этапа: Уравнения для скорости и момента в функции времени на данном этапе: 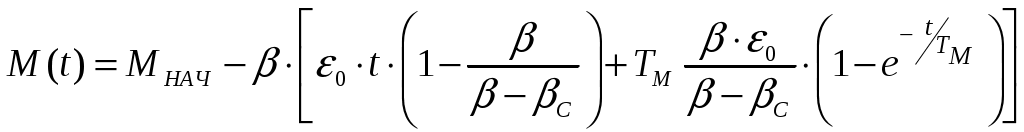 . (9) . (9)I-й этап заканчивается в момент времени (t1 на рис. 6), когда двигатель выходит на характеристику заданного режима в точке «б». Длительность этапа : Для расчёта переходного процесса нужно определить новое численное значение величины 0. Дальнейший разгон двигателя протекает при постоянном значении 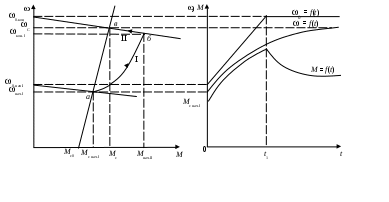 Рисунок 6. Статические характеристики и динамическая характеристика и графики переходных процессов при увеличении скорости привода В). Торможение системы от начальной скорости нач, которую она имела в исходном установившемся режиме работы, до полной остановки представлен на рис. 7. Переходный процесс разбивается на два этапа. На I-м этапе (0 ≤ t ≤ t2) 0 снижается по линейному закону от 0. нач до 0. При торможении ускорение 0 < 0 (его рассчитали в самом начале расчёта переходных процессов). Начальные условия I-го этапа: Для скорости и момента в функции времени на этом этапе справедливы выражения (8) и (9). Заканчивается этап при На II этапе (t>t2) переходный процесс протекает при ω0 = 0. Двигатель работает в режиме динамического торможения. Скорость и момент на данном этапе описываются выражениями (6) и (7). Необходимо отметить, что величины нач и Мнач, входящие в эти уравнения, определяются координатами точки «б» (см. рис. 7), а ’С и М’С – координатами точки «в» условного установившегося режима. Точка «в» находится в месте пересечения продолжений механических характеристик двигателя и РМ. Для определения координат точки «в» при моменте Мс ≠ 0 лучше выполнить построение на миллиметровке, или, что менее точно, на листе в клеточку. Нарисуйте в масштабе механическую характеристику двигателя, проходящую через начало координат, и механизма. Точка их пересечения в четвертом или во втором квадранте даст координаты скорости ’С и момента М’С. Расчёт скорости вращения и электромагнитного момента при торможении на II этапе переходного процесса заканчивают, когда они приблизительно станут равными 0. Далее привод остается неподвижным. Длительность переходного процесса на этом этапе: 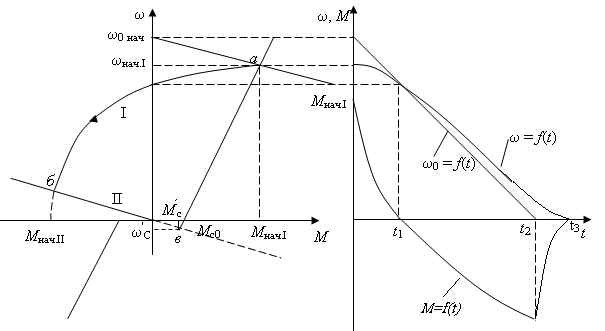 Рисунок 7. Статические и динамическая характеристики, графики переходных процессов при торможении до полной остановки Г). Снижение скорости системы от начальной скорости исходного установившегося режима да некоторой конечной, ненулевой. Переходный процесс (см. рис. 8) разбивается на два этапа. На I-м этапе (0 ≤ t ≤ t2) 0 снижается от 0.нач до 0.кон с постоянным замедлением 0. Начальные условия I-го этапа: Начальные условия I-го этапа: Зависимости (t) и М(t) описываются выражениями (8) и (9). Заканчивается I-й этап при ω0 = ω0. кон, длительность его: 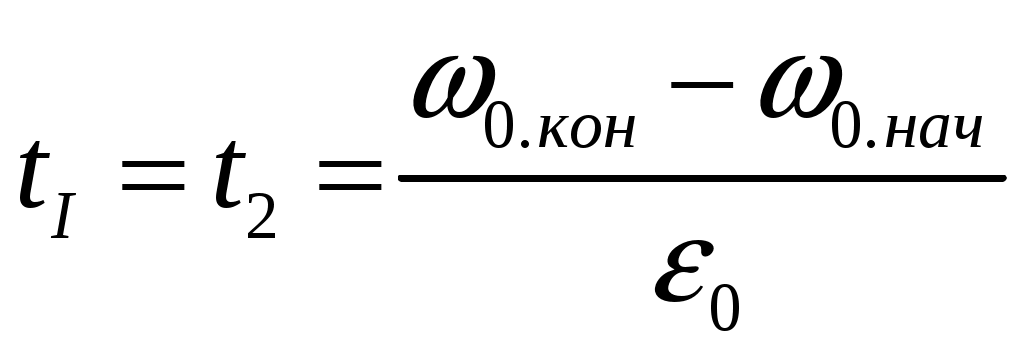 . .Начальный (исходной) и конечной точками I-го этапа являются соответственно точки «а» и «б» с соответствующими координатами. На II-м этапе (t>t2) происходит дальнейшее снижение скорости двигателя при работе его с постоянным значением ω0 = ω0.кон. Скорость и момент двигателя на данном этапе описываются выражениями (6) и (7). Начальные и установившиеся значения скорости и момента определяются соответственно координатами точек «б» и «в», длительность этапа: tп = (3÷4) Tм. 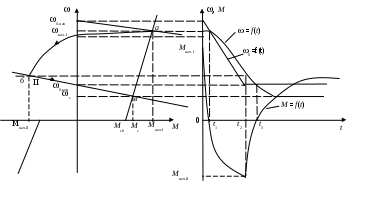 Рисунок 8.Статические и динамическая характеристики, и графики переходных процессов при снижении скорости ЭП Д). Реверс системы. Осуществляется линейным изменением 0 от О.НАЧ до О.КОН (см. рис. 9) со сменой её знака в процессе изменения. I-й этап реверса – торможение до нулевой скорости (0 ≤ t ≤ t3) описан выше. Дальнейший ход переходного процесса определяется соотношением между моментами двигателя и РМ при достижении нулевой скорости в момент времени t3. При М(0) а) этап линейного нарастания момента двигателя при нулевой его скорости от значения М(0) до Мс0, II-й этап реверса (t3 ≤ t ≤ t4); 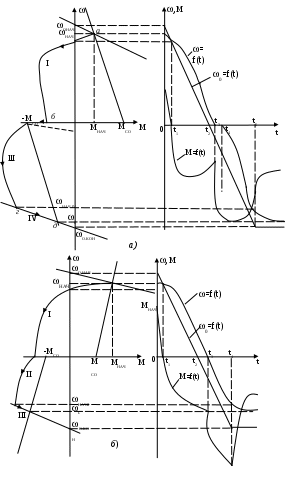 Рисунок 9. Статические, динамические характеристики и графики переходных процессов при реверсе системы: а – при М < МСО ( = 0); б – при М > МСО ( = 0) б) этап разгона при нарастании 0, III-й этап реверса (t4 ≤ t ≤ t5); При расчёте применить уравнения (1, 2) или (10, 11). в) этап разгона при постоянном значении 0, IV-й этап реверса (t>t5). Применить уравнения (6, 7). Длительность II-го этапа: Определить численное значение 0 < 0. На этом этапе законы изменения скорости и момента: III-й и IV-й этапы реверса (разгон на отрезке (t4 ≤ t ≤ t5) и при t > t5) протекают аналогично описанному в п.1. данного раздела (пуск системы ЭП). При М(0) Мc 0 (см. рис. 9, б) этап нулевой скорости при разгоне отсутствует. В этом случае переходный процесс разгона разбивается на два этапа: а) этап разгона при линейном изменении 0 во времени (II-й этап реверса, (t3 ≤ t ≤ t4); б) этап разгона при постоянном значении 0 (III-й этап реверса, t > t4). Начальные условия II-го этапа: Скорость и момент на данном этапе описываются выражениями: 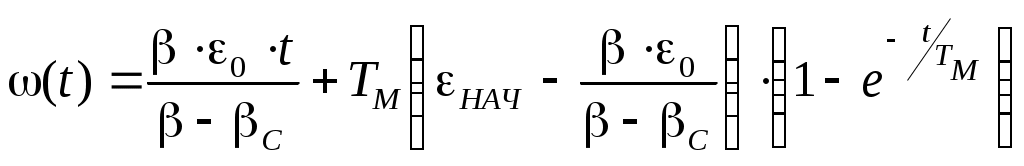 , (10) , (10)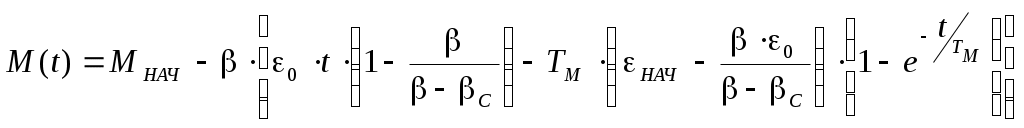 . (11) . (11)Длительность II-го этапа: 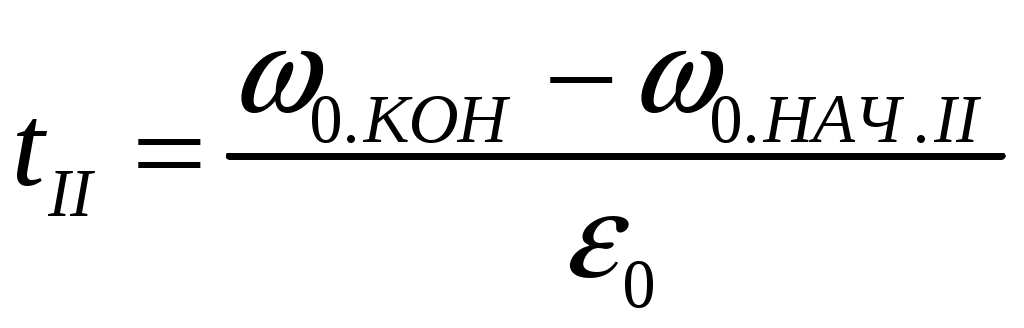 , ,где Третий этап протекает аналогично III-му этапу случая, описанного в п. 1 настоящего раздела. Предпочтительный вариант. Еще одним способом расчёта реверса двигателей будет следующий вариант. Ротор (якорь) двигателя останавливают по способу, предложенному в п. 3 настоящего раздела «Торможение системы от начальной скорости нач, которую она имела в исходном установившемся режиме работы, до полной остановки. Затем разгоняют ротор в противоположном направлении (см. 1. Разгон системы из неподвижного состояния). Общее количество этапов переходного процесса при этом будет 5 (см. рис. 10). 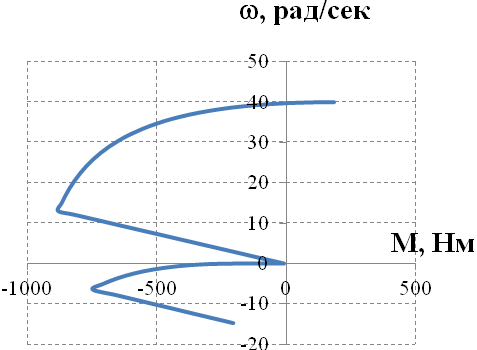 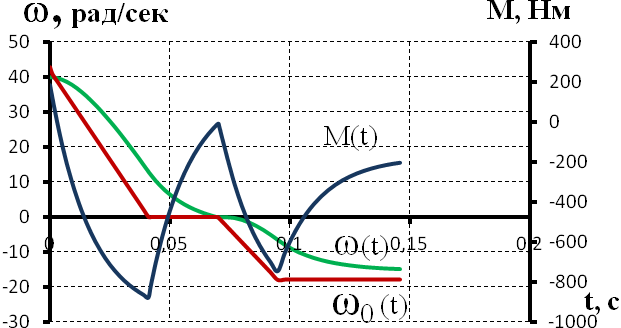 Рисунок 10 Динамические характеристики и графики переходных процессов при реверсе системы При рассмотрении переходных процессов в зоне отрицательных скоростей можно воспользоваться этой же методикой и этими же формулами расчёта. При этом следует учесть, что скорости (ω и ω 0), ускорения (НАЧ и 0), моменты (двигателя и РМ) будут иметь обратные знаки по сравнению со знаками, которые они имели бы при рассмотрении процесса в зоне положительных скоростей (ускорение будет отрицательно, замедление положительно, движущий момент отрицателен, тормозной положителен и т.д.). Это справедливо как для текущих их значений, так и для значений во всех характерных точках (начальных, установившихся и т.д.). Вместе с этим коэффициенты жесткости и С остаются неизменными. Возможен и другой подход: учитывая, что моменты сопротивления РМ при положительной и отрицательной скоростях одинаковы, расчёт проводят для случая положительных скоростей. Далее – при построении графиков зависимости (t), M(t) – меняют знаки скорости и момента на обратные. Выводы: После расчёта переходных процессов необходимо оценить быстродействие спроектированной системы, т.е. определить суммарное время переходных процессов tПП. и найти его значение в % от времени цикла, где Кроме того, необходимо оценить, не превышает ли максимальные значения момента двигателя в переходных процессах значения МДОП. 6.4 Комментарии к п. 12 - 24 К п.12. Двигатель проверяется на нагрев одним из методов, изложенных в работах [1; 2; 4; 21]. При этом необходимо учитывать изменение условий охлаждения при паузах и изменениях скорости, а в случае регулирования скорости потоком возбуждения в диаграмму моментов вводить поправки, которые сделали бы ординаты кривой моментов пропорциональными току. При проверке двигателя на нагрев по методу эквивалентных величин (тока, мощности, момента) вычисленные эквивалентный ток, момент, мощность следует сравнить с допустимыми по условиям нагрева током, моментом, мощностью, приводимыми в каталогах для номинального ПВ, после пересчета их на фактическую ПВ%, найденную из нагрузочной диаграммы привода. Ниже приведена методика проверки на нагрев предварительно выбранного двигателя по методу эквивалентного момента. Для проверки необходимо: Выполнить линеаризацию построенной в отдельной системе координат кривой М(t) за цикл работы с учетом установившихся режимов стандартными фигурами – треугольник, трапеция, прямоугольник (15-20 фигур). Для каждой стандартной фигуры определить эквивалентный момент Мэ i или ток Iэ i. При этом   , , где Mм, М1, М2 – максимальные значения моментов в треугольниках и трапециях. Аналогично можно определить значения эквивалентных токов якоря для МПТ или тока ротора для АД. Определить эквивалентный момент за цикл: 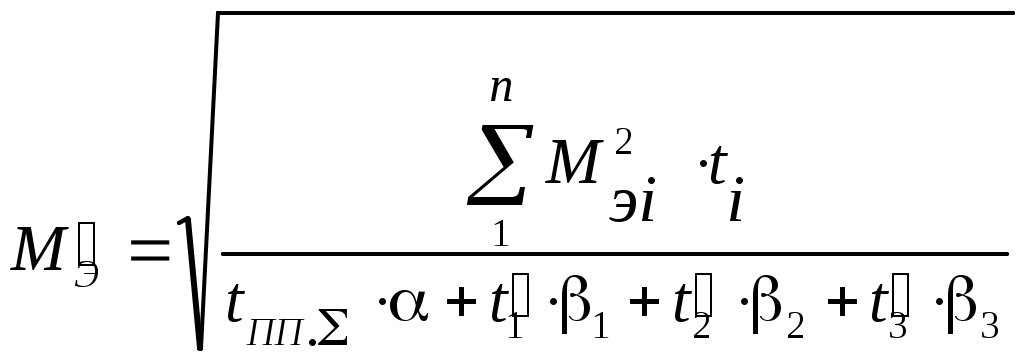 , ,где ti – отрезок времени, на который опирается i-я стандартная фигура; n – число этих фигур; tПП.Σ – суммарное время переходных процессов за цикл; α и βi – коэффициенты учитывающие ухудшение (улучшение) условий охлаждения двигателя в переходных процессах и в статических режимах работы при ωc i≠ ωн; где 0 – коэффициент, учитывающий ухудшение условий охлаждения двигателя во время паузы. Для двигателей закрытого исполнения с естественным охлаждением или самовентиляцией принимают β0 ≈ 0,5. Определить фактическую продолжительность включения: 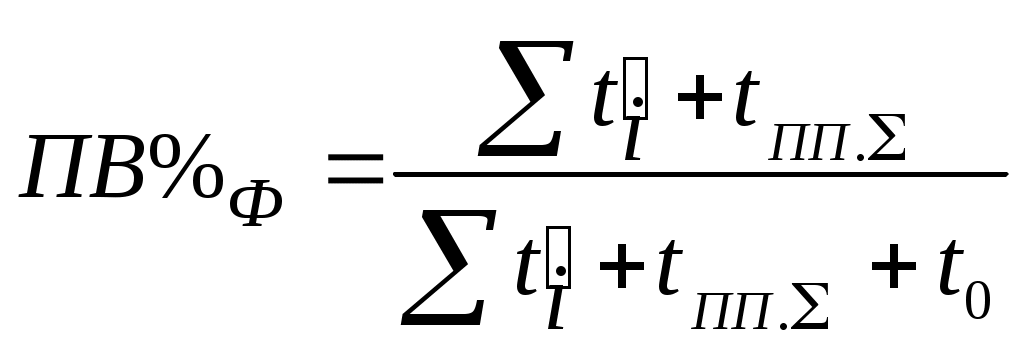 . .Пересчитать найденное значение 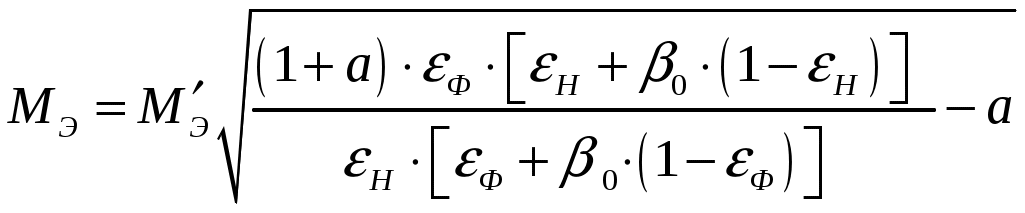 , ,где где kн, Vн – номинальные постоянные и переменные потери мощности [1, с. 345]. Формула действительна для двигателей с естественным охлаждением и самовентиляцией. Проверить предварительно выбранный двигатель на нагрев. Условие проверки: где МН2 – номинальный электромагнитный момент второго двигателя ближайшей меньшей мощности. Ранее выбранный двигатель был проверен на перегрузочную способность. Если выбранный двигатель удовлетворяет условиям выполняемых проверок, то его следует рекомендовать к внедрению. Если двигатель по нагреву не подходит, необходимо или снизить интенсивность переходных процессов (при этом увеличится их длительность и уменьшится производительность РМ), или взять двигатель большей мощности и повторить расчёты. При проверке двигателей переменного тока по перегрузочной способности обязательно следует учитывать возможное снижение напряжения питающей сети (на 10%). К п.13. Для построения структурной схемы электропривода двигателя постоянного тока независимого возбуждения необходимо написать уравнение динамической механической характеристики этого двигателя совместно с уравнением движения в операторной форме в предположении жестких механических связей и с учетом ЭДС управляемого преобразователя и его передаточной функции. Структурная схема электропривода с асинхронным двигателем должна быть построена для области рабочих скольжений также на основании уравнения динамической механической характеристики, записанного в операторной форме. При составлении структурных схем можно воспользоваться уравнением динамической механической характеристики, а также уравнениями обобщенной линеаризованной системы УП–Д [1], подставив в них параметры ТЭ, ТП и , соответствующие заданной системе электропривода. Примеры структурных схем обобщенной линеаризованной системы УП–Д приведены в [1, с. 427-454]. На приведенных в проекте структурных схемах указать численные значения входящих в них величин. К п.14. Точность поддержания скорости привода в установившемся режиме работы (статическая ошибка по скорости) определяется по соотношению: 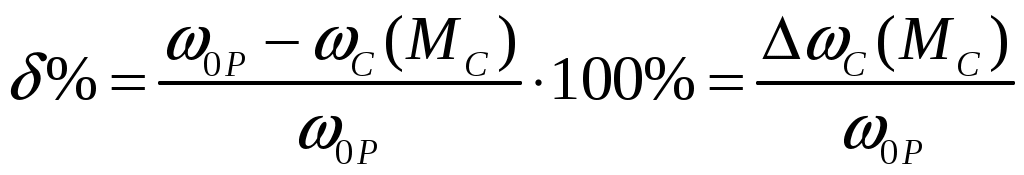 , ,где ω0р, ωс(МС), Δωс(МС) – скорость идеального х.х., статическая скорость и статическое падение скорости вращения при М = МН на i-ой регулировочной характеристике. К п.15. При выборе замкнутой системы рекомендуется принимать систему с подчиненным регулированием координат. Выполнить поставленные в задании требования помогает применение стандартных настроек. Поскольку на практике чаще всего используется стандартная настройка на технический оптимум, когда соотношение постоянных времени контуров регулирования а=2, в курсовом проекте также рекомендуется контур скорости настраивать на технический оптимум. При отсутствии такой возможности последовательную коррекцию нужно дополнить параллельной. При питании двигателя постоянного тока в разомкнутой системе от тиристорного преобразователя рекомендуется применить замкнутую систему ТП–Д с подчиненным контуром регулирования тока и внешним контуром регулирования скорости (рис. 15). При частотном управлении асинхронным двигателем может быть использована система частотного регулирования момента с автономным инвертором напряжения (АИН), дополненная отрицательной обратной связью по скорости. Структурная схема системы представлена (см. рис. 16, а), где Wрс(р) = Крс/(Тфр + 1) – передаточная функция пропорционального регулятора скорости, причем в ней учтена малая постоянная времени ТФ фильтра в цепи обратной связи по скорости. Принципиальная блок-схема изображена на рис. 16, б. WPC  C    UЗС М  -         - -   МСО KОС СТ    а)            ROCT COCT            RO.CC         RЗС ОВТГ  |
