ТОЭ МУ КуР (Леонов Е. Н.) Тюмень 2019 ТИУ. Методические указания по выполнению курсовой работы по дисциплине Теоретические основы электротехники
 Скачать 1.45 Mb. Скачать 1.45 Mb.
|
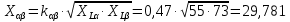  . .                   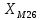    Рисунок 2. Исходная расчетная схема цепи Для удобства можно обозначить все величины в символической форме. Следует обратить внимание на знаки у емкостных сопротивлений (они берутся со знаком «минус»). Величина взаимной индуктивности для расчетов может браться как со знаком «плюс», так и со знаком «минус» в зависимости от направления протекании тока по индуктивно связанным элементам. Поэтому для записи взаимной индуктивности можно использовать формулу)  . .Расчетная схема цепи в форме записи с символическими величинами необязательна, но может быть более наглядна для расчетов. Образец такой схемы приведен на рисунке 3. Если первоначально составляется схема с символическими величинами, то и в дальнейших построениях должна фигурировать именно эта схема.            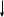      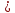 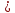 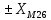  Рисунок 2. Исходная расчетная схема цепи с символическими величинами 2. Расчет методом контурных токов (МКТ) цепи переменного тока производится так же, как и цепи постоянного тока, только вместо ЭДС, токов и сопротивлений берутся соответствующие величины, записанные в символической форме. Сущность метода состоит в уменьшении числа совместно решаемых уравнений, путем замены реальных токов ветвей расчетными контурными токами. 2.1. Определяем количество уравнений, которое необходимо и достаточно согласно МКТ, для исходной схемы (рисунок 2 или 3): 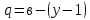 , ,где 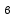 - число ветвей - число ветвей 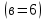 ; ;у - количество узлов  , поэтому: , поэтому: . .2.2. Выбираем направление контурных токов в схеме (либо по часовой стрелке, либо - против), например как на рисунке 4 и составляем систему:                   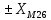  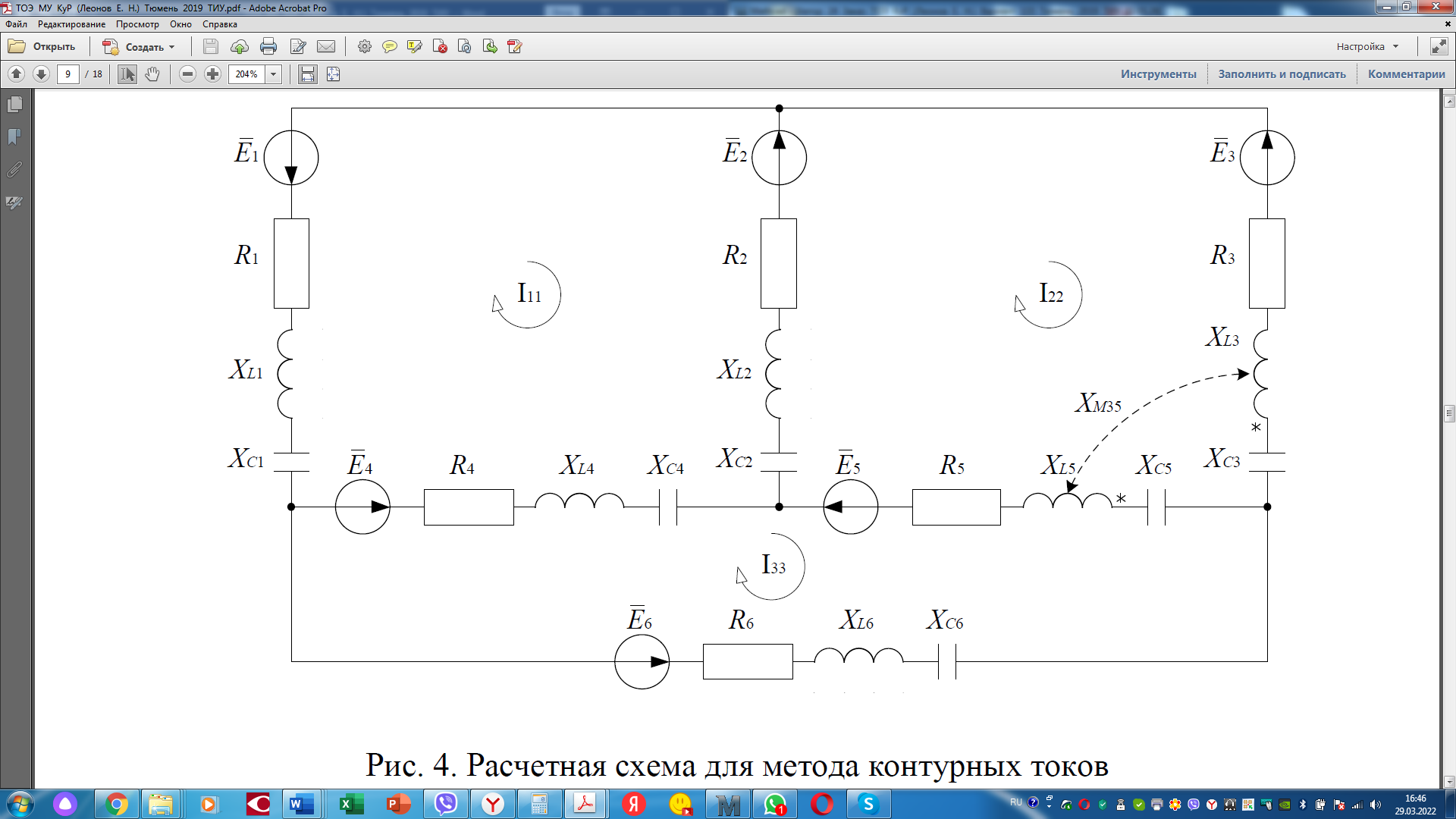 Рисунок 4. Расчетная схема для метода контурных токов 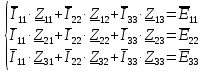 , (1) , (1)где  , , 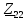 , ,  - комплексы собственных сопротивлений контуров; - комплексы собственных сопротивлений контуров;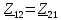 , , 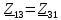 , ,  - комплексы взаимных (смежных) сопротивлений контуров; - комплексы взаимных (смежных) сопротивлений контуров;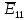 , , 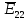 , , 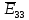 - комплексы контурных ЭДС. - комплексы контурных ЭДС.2.3. Комплексы собственных сопротивлений контуров: 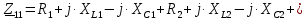  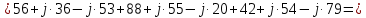 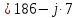  ; ; 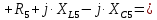 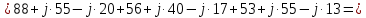 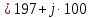  ; ;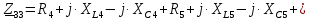  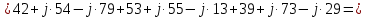 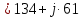  . .Взаимное индуктивное сопротивление учитывается в собственном сопротивлении только тогда, когда есть индуктивные связи внутри рассматриваемого контура. При этом учитывается правило знаков: если контурный ток одинаково ориентирован относительно одноименных полюсов катушек, то  берётся со знаком плюс, и наоборот, при разной ориентации, это сопротивление учитывается со знаком минус. Так как в контуре взаимная индуктивность встретится дважды, то она умножается на два. берётся со знаком плюс, и наоборот, при разной ориентации, это сопротивление учитывается со знаком минус. Так как в контуре взаимная индуктивность встретится дважды, то она умножается на два.2.4. Комплексы взаимных сопротивлений контуров, рассматриваемой схемы: 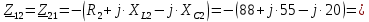 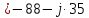  ; ;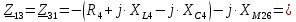 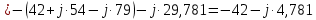  ; ;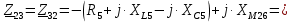 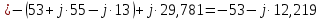  . .В некоторых случаях взаимных сопротивлений между контурами может и не быть, или в качестве взаимного сопротивления может фигурировать только взаимная индуктивность (в схеме для данной работы последний случай невозможен) Слагаемые в скобках определяются по правилам цепей постоянного тока. А взаимные индуктивные составляющие - в зависимости от ориентации контурных токов относительно одноименных полюсов катушек, также по правилу знаков (если контурные токи одинаково ориентированы относительно одноименных полюсов катушек, то  берётся со знаком плюс, и, наоборот, при разной ориентации контурных токов, это сопротивление учитывается со знаком минус). берётся со знаком плюс, и, наоборот, при разной ориентации контурных токов, это сопротивление учитывается со знаком минус).2.5. Контурные ЭДС, представляющие собой алгебраические суммы ЭДС, входящих в контуры. Комплексы контурных ЭДС входящая в эту сумму, берутся с положительным знаком, если их направление совпадает с контурным током, и, наоборот, с отрицательным - если их направление навстречу контурному току. Например для рассматриваемого варианта:  ; ;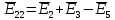 ; ;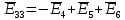 . .Для расчета контурных ЭДС необходимо рассчитать ЭДС всех источников:  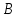 ; ;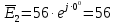 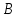 ; ; 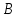 ; ; 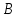 ; ;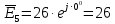 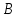 ; ;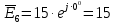 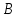 . .Тогда: 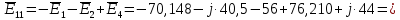  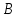 ; ; 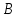 ; ;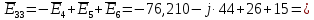  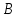 . .2.6. После нахождения всех вспомогательных величин, делаем их подстановку в систему (1). Система (1) решается относительно контурных токов 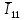 , ,  , ,  в среде Mathcad, там же приведен расчет модулей и фаз контурных токов: в среде Mathcad, там же приведен расчет модулей и фаз контурных токов: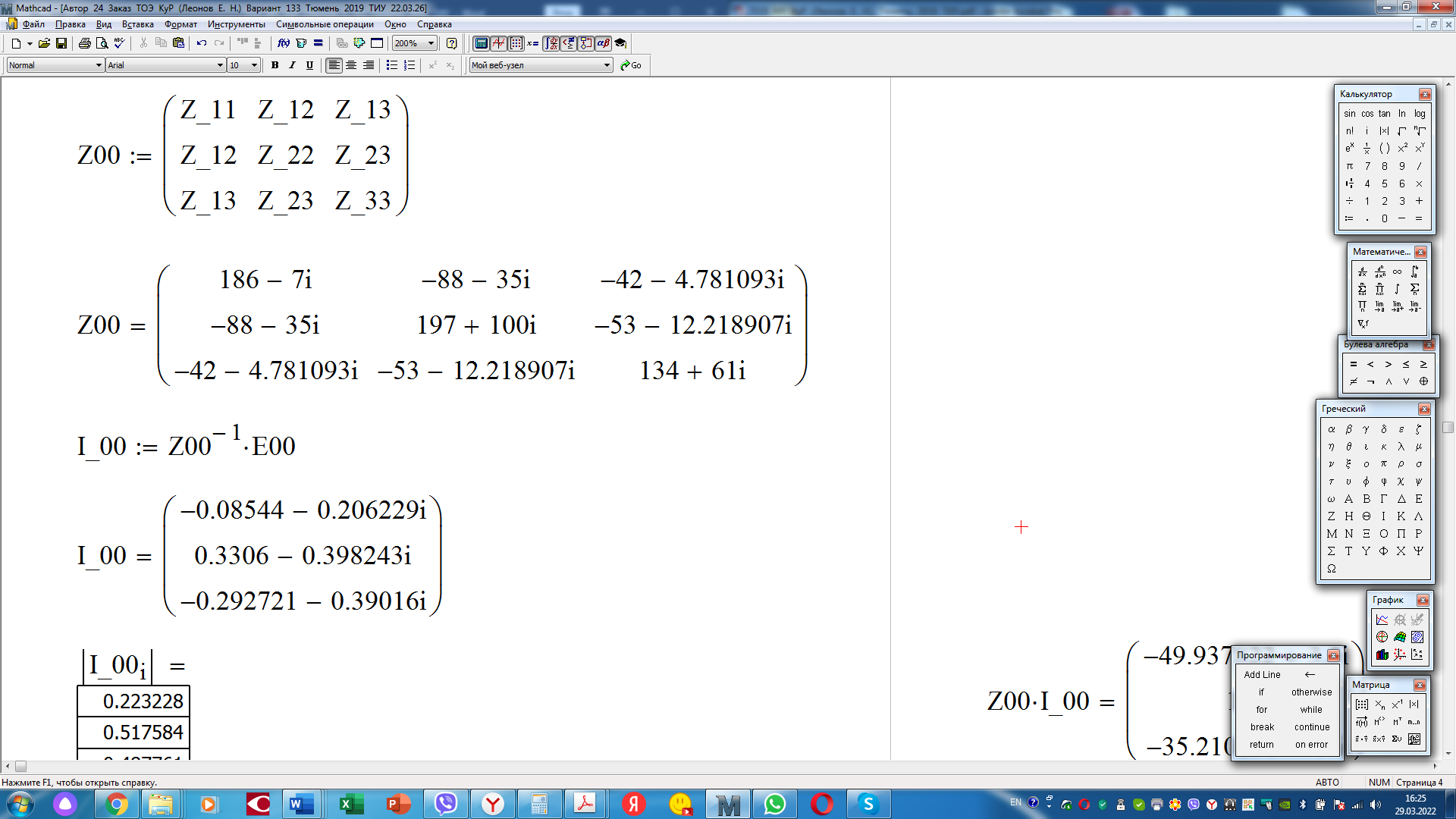 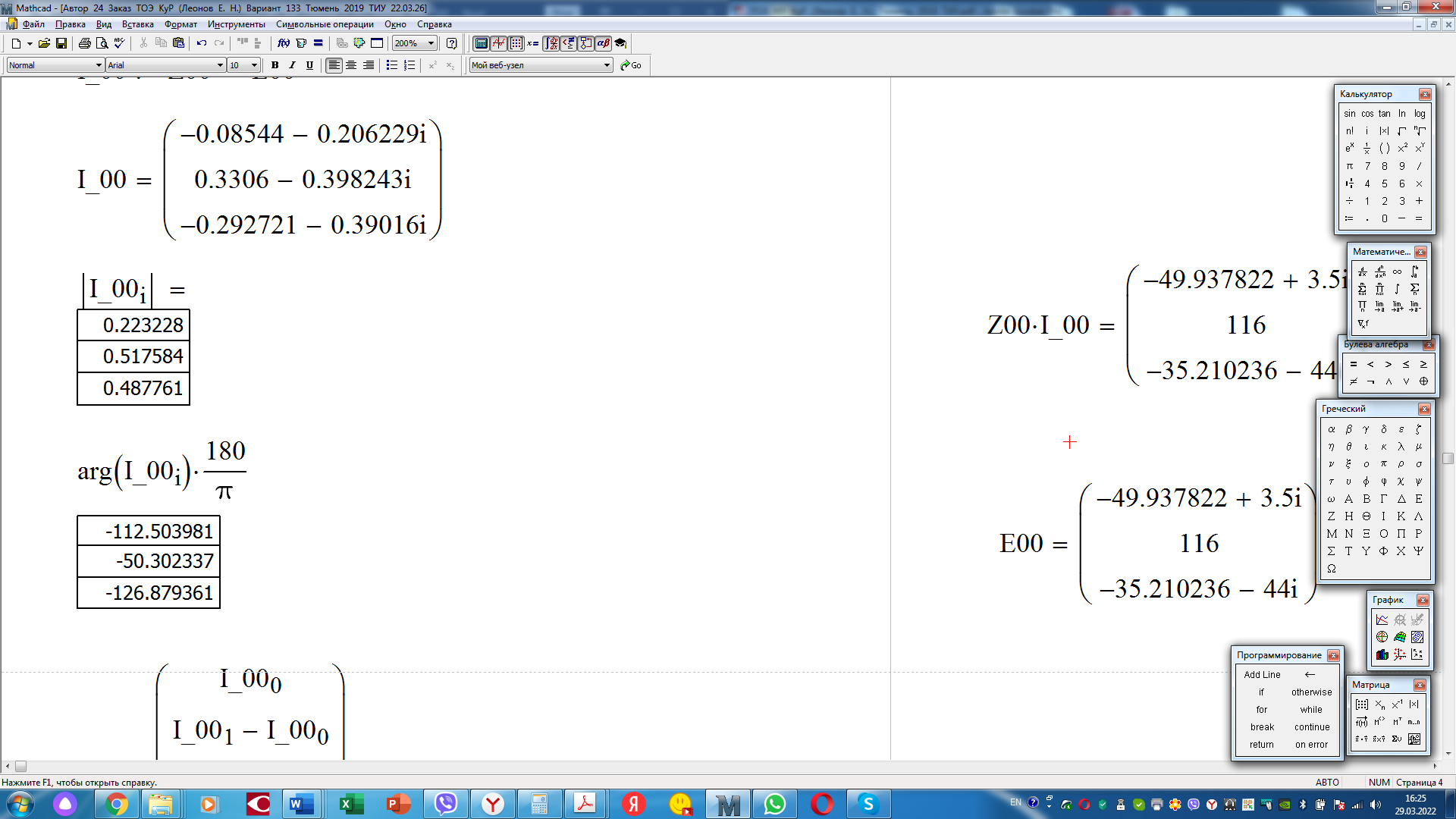 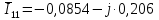  ; ;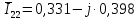  ; ;  ; ;2.7. Для вычисления токов в ветвях предварительно зададимся их направлениями, например, как показано на рисунке 2. Тогда токи в ветвях схемы определяются как алгебраическая сумма контурных токов, протекающих через ветвь:   ; ;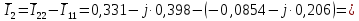 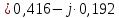  ; ;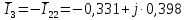  ; ; 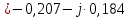  ; ;   ; ;  . .Отрицательные знаки, полученные при расчетах контурных токов и токов в ветвях указывают на то, что их действительные направления противоположны тем, которые ранее выбраны в качестве положительных. 2.8. Необходимо привести аналитические выражения для мгновенных значений токов ветвей 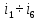 . Например для тока . Например для тока 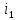 аналитическое выражение имеет вид: аналитическое выражение имеет вид: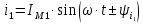 , ,где 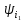 - начальная фаза тока - начальная фаза тока 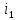 (аргумент комплексного числа); (аргумент комплексного числа); - амплитудное значение тока - амплитудное значение тока 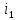 ; ;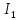 - действующее значение тока - действующее значение тока 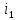 , полученное в результате расчетов (модуль комплексного числа). , полученное в результате расчетов (модуль комплексного числа).Аналитические выражения для всех токов, протекающих по ветвям. 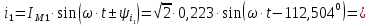 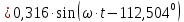  ; ; 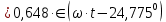  ; ; |
