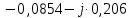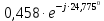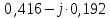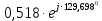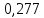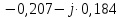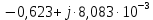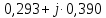ТОЭ МУ КуР (Леонов Е. Н.) Тюмень 2019 ТИУ. Методические указания по выполнению курсовой работы по дисциплине Теоретические основы электротехники
 Скачать 1.45 Mb. Скачать 1.45 Mb.
|
   ; ;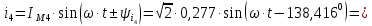 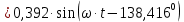  ; ;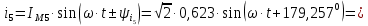   ; ;   . .3. Прежде, чем составлять систему уравнений по законам Кирхгофа, определяется общее количество необходимых уравнений. По первому закону Кирхгофа для схемы (рисунок 2): 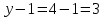 . .где  - число узлов в схеме. - число узлов в схеме.По второму закону Кирхгофа:  . .По первому закону Кирхгофа для любого узла: 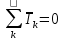 . (2) . (2)По второму закону Кирхгофа: 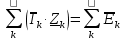 . (3) . (3)3.1. Раскроем подробнее выражение (2) для узлов. Для записи уравнения необходимо учитывать направления токов в ветвях. Токи алгебраически суммируются, направленные к данному узлу берутся положительными, а от узла - отрицательными:  ; (4) ; (4) ; ; . .3.2. Система (3) составляется так же, как и в цепях постоянного тока, но появляются слагаемые, связанные с взаимной индуктивностью. Падение напряжения для собственного сопротивления ветви в системе (3) берется положительным, если ток в ветви совпадает с направлением обхода контура, и отрицательным, если не совпадает. ЭДС в выражении (3) берется положительной, если она совпадает с направлением обхода контура и отрицательном при противоположном направлении. Взаимные индуктивности учитываются по следующему правилу: если направление обхода элемента  и ток в ветви с элементом и ток в ветви с элементом 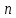 одинаково ориентированы по отношению к одноименным полюсам индуктивности, то одинаково ориентированы по отношению к одноименным полюсам индуктивности, то  берётся с положительным знаком, и, наоборот, если направление обхода элемента берётся с положительным знаком, и, наоборот, если направление обхода элемента  и ток в ветви с элементом и ток в ветви с элементом 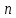 по разному ориентированы по отношению к одноименным полюсам индуктивности, то по разному ориентированы по отношению к одноименным полюсам индуктивности, то  имеет знак минус. имеет знак минус.Уравнение для первого независимого контура (при обходе контура по часовой стрелке и направлении токов в ветвях, указанных на рисунке 2): 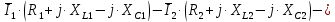 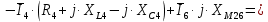 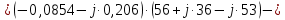 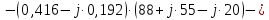 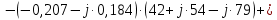 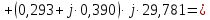 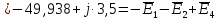 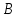 . (5) . (5)Уравнение для второго контура: 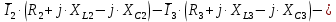 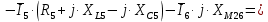   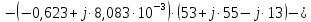   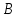 . (6) . (6)Уравнение для третьего контура: 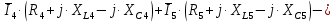  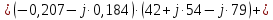  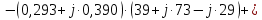   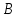 . (7) . (7)Погрешность выполнения равенств (4) - (7) находится отдельно для вещественных и мнимых частей, в каждом случае она не должна превышать пяти процентов. В данном случае эта погрешность равна 0 (меньше, чем три знака после запятой). 4. Векторная диаграмма токов и топографические диаграммы напряжений строится на основании уравнений расчетов п. 2.6 и п. 3.2. На комплексной плоскости выбираются масштабы для векторов тока и напряжения и в соответствии с этим откладываются в комплексной плоскости. При этом, для удобства построения и чтения чертежей рекомендуется векторную диаграмму токов и топографические диаграммы напряжений строить разным цветом. Или как вариант - разнести топографические диаграммы на три разных рисунка (векторная диаграмма токов при этом строится на каждом рисунке). 4.1. Векторная диаграмма - это совокупность векторов, отображающих синусоидальные функции одной частоты. Векторная диаграмма токов строится на основании расчетов п. 2.6, при этом все вектора токов откладываются из начала координат. 4.2. Топографическая диаграмма - это векторная диаграмма напряжений, построенная на комплексной плоскости и учитывающая расположение элементов в электрической схеме. Топографическая диаграмма строится по следующим правилам: а) потенциал одной из точек контура принимается равной нулю; б) определяются комплексные значения потенциалов всех точек схемы относительно точки, потенциал которой принят за нуль; в) найденные значения потенциалов точек переносятся на комплексную плоскость и соединяются в соответствии с расположением этих точек на схеме. Топографическая диаграмма строится на основании уравнений (5) - (7). При правильном построении вектора падения напряжения на элементах, просуммированные по правилу многоугольника, например, в левой части выражения (5), совпадут с суммой векторов ЭДС из правой части. Т. о., векторная диаграмма является не только иллюстрацией к решенной задаче, но служит для проверки правильности её решения (несовпадение векторов в правой и левой части уравнений говорит о допущенной где-то ошибке). 5. Для проверки достоверности полученного результата составляется баланс мощностей. Из закона сохранения энергии очевидно, что для любого момента времени сумма мгновенных мощностей всех приемников энергии равна сумма мгновенных мощностей всех источников. Это положение справедливо как для активных, так и для реактивных мощностей. Совпадение в расчетах правой и левой частей уравнений с погрешностью 5 % можно считать удовлетворительным. Энергетический баланс мощностей, развиваемых источниками ЭДС и потребляемых в цепи, проверяется для каждого контура в отдельности следующим образом: 5.1. Для активных мощностей: 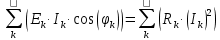 . (8) . (8)В правой части уравнения (8) - арифметическая сумма мощностей, рассеиваемых на активных сопротивлениях. В левой части уравнения (8) - алгебраические суммы активных мощностей источников. Если направление источника ЭДС и тока совпадают, то произведение берется со знаком плюс, если направления не совпадают, то - со знаком минус. Если мощность отдельного источника окажется отрицательной  , то это означает, что данный источник потребляет активную мощность (т. е. это электродвигатель). , то это означает, что данный источник потребляет активную мощность (т. е. это электродвигатель). 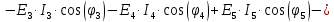   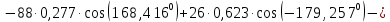 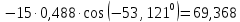 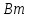 ; ; 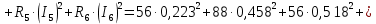 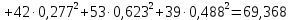 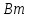 . .При составлении данного уравнения были учтены противоположные направления тока 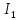 и источника и источника 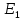 , тока , тока  и источника и источника 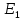 , тока , тока  и источника и источника 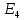 , тока , тока 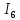 и источника и источника  . .5.2. Для реактивных мощностей: 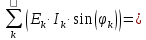 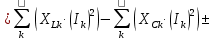 (9) (9)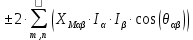 . .В левой части уравнения (9) - алгебраическая сумма реактивных мощностей источников. Если мощность отрицательная 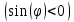 , значит источник потребляет реактивную мощность. , значит источник потребляет реактивную мощность.В правой части (9) первое слагаемое - индуктивная реактивная мощность, второе слагаемое - емкостная реактивная мощность, третье слагаемое - реактивная мощность, обусловленная индуктивной связью между катушками ( 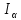 , , 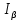 - токи взаимосвязанных катушек, - токи взаимосвязанных катушек, 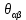 - угол сдвига фаз между токами). При расчете третьего слагаемого знак плюс берётся при согласном включении катушек, а минус - при встречном включении. - угол сдвига фаз между токами). При расчете третьего слагаемого знак плюс берётся при согласном включении катушек, а минус - при встречном включении. 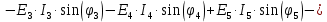   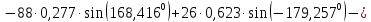   ; ; 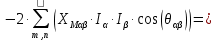    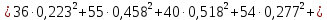 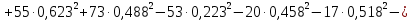  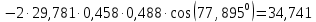  . .5.3. Результаты всех расчетов свести в таблицу 5. Таблица 3 Результаты расчетов токов в ветвях схемы   ; ;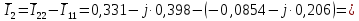 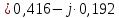  ; ;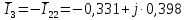  ; ; 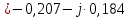  ; ;   ; ;  . .
| ||||||||||||||||||||||||||||||||||

 ,
, 
 ,
,