МУ к ЛР Электротехника ИБб. Методические указания по выполнению лабораторных работ для обучающихся по направлению 10. 03. 01 Информационная безопасность, профиль подготовки Комплексная защита объектов информатизации (в сфере техники и технологии). Иркутск. Ирниту, 2018. 40 с
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
Контрольные вопросы
Лабораторная работа № 4 ИССЛЕДОВАНИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ R, L И С. Цель работы: Экспериментально проверить основные теоретические соотношения в электрической цепи переменного тока при последовательном соединении индуктивной катушки и конденсатора. Освоить методику построения векторных диаграмм. Исследовать цепь в режиме резонанса. Краткие теоретические сведения. R L C e(t) u I uL uC uR Рис. 4.1 Последовательный колебательный контур представляет собой электрическую цепь, содержащую индуктивную катушку и конденсатор, включенные последовательно с источником энергии (рис. 4.1). Последовательно с реактивными элементами включен резистор R. В ряде случаев этот резистор включается намеренно, а в ряде случаев он может представлять собой суммарное сопротивление контура, определяемое сопротивлением всех проводов контура и внутренним сопротивлением источника. При последовательном соединении через все элементы цепи течет один и тот же ток, а мгновенное значение напряжения на входе цепи согласно второму закону Кирхгофа будет равно: u = uR + uL + uC, где uR - падение напряжения на резистивном элементе, uL - падение напряжения на индуктивности, uC - падение напряжения на емкости. Поскольку мгновенные значения напряжений и токов изменяются в зависимости от времени, то расчеты электрических цепей переменного тока выполняются с использованием комплексных амплитуд. В комплексной форме второй закон Кирхгофа запишется: 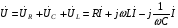 Напряжение на резистивном элементе совпадает по фазе с током, напряжение на индуктивности опережает ток на 90, а напряжение на емкости отстает от тока на 90. Поскольку любой реальный реактивный элемент (катушка или конденсатор) обязательно имеет некоторое ненулевое активное сопротивление, сдвиг фаз между током и напряжение на этих элементах оказывается меньше 90о. Чем ближе к 90о будет сдвиг фаз, тем ближе будут свойства реального реактивного элемента к идеальному. Количественно степень приближения свойств реальных элементов к идеальным оценивается их добротностью, которая определяется как модуль тангенса сдвига фаз между током и напряжением на зажимах соответствующего элемента 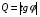 . .Исходя из этого, добротность катушки определится выражением 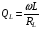 , ,где L – индуктивность катушки; RL – активное сопротивление катушки. Добротность конденсатора определится выражением 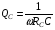 , ,где С – емкость конденсатора, RC – активное сопротивление конденсатора. Реально добротность индуктивных катушек лежит в пределах от нескольких десятков до нескольких сотен, а добротность конденсаторов от нескольких сотен до нескольких тысяч. Полное комплексное сопротивление цепи определится выражением: 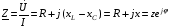 где R - активная составляющая полного сопротивления, хL=L – индуктивная составляющая, хC=1/C - емкостная составляющая полного сопротивления цепи. Модуль комплексного сопротивления z находится как 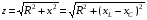 , ,а аргумент 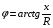  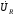 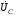 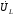 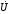 φ Рис. 4.2 Угол сдвига фаз между током и напряжением на входе цепи зависит от соотношения между активным, индуктивным и емкостным сопротивлениями. В зависимости от величины этих сопротивлений в цепи можно выделить три характера нагрузки. 1. Пусть xL>xC, в этом случае напряжение на индуктивности больше напряжения на емкости UL>UC, следовательно, реактивная составляющая напряжения равная Up(L) = UL - UC имеет индуктивный характер, и напряжение на входе цепи опережает по фазе ток . Характер цепи будет активно-индуктивным. Векторная диаграмма для активно-индуктивного характера нагрузки представлена на рис. 4.2  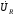 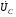 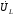 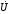 φ Рис. 4.3 2. Пусть xL< xC, в этом случае В этом случае напряжение на индуктивности меньше напряжения на емкости UL < UC, следовательно, реактивная составляющая напряжения равная Up(L) = UL - UC имеет емкостный, и напряжение на входе цепи отстает по фазе от тока < . Характер цепи будет активно- емкостным. Векторная диаграмма для активно-емкостного характера нагрузки представлена на рис. 4.3.  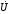 = =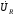 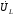 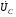 Рис. 4.4 3. Пусть xL=xC, в этом случае индуктивное и емкостное напряжения равны по величине UL = UC, характер цепи будет активным = , и в цепи имеет место резонанс напряжений. Резонансом называют такой режим работы электрической цепи, в котором ток и напряжение на входе цепи совпадают по фазе. Резонанс напряжений возникает в цепи, содержащей последовательно соединенные индуктивный и емкостный элементы, при условии равенства индуктивного и емкостного сопротивлений. При xL=xCполное сопротивление цепи будет минимальным и носить активный характер 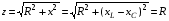 , ,следовательно ток будет максимальным 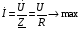 . .Максимум тока является признаком резонанса напряжений. Равенство индуктивного и емкостного сопротивлений является условием резонанса напряжений 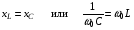 . .Исходя из этого соотношения, резонансная частота определится как 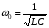 , или , или 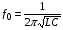 . .Если реактивные сопротивления 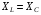 превосходят при резонансе активное сопротивление: то напряжение на зажимах катушки и конденсатора могут существенно превышать напряжение на входе цепи. превосходят при резонансе активное сопротивление: то напряжение на зажимах катушки и конденсатора могут существенно превышать напряжение на входе цепи.Превышение напряжения на реактивных элементах над напряжением на входе принято характеризовать величиной 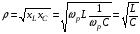 , ,называемой волновым или характеристическим сопротивлением цепи. Волновое сопротивление численно равно индуктивному или емкостному сопротивлению цепи на резонансной частоте. Кратность превышения напряжения на зажимах индуктивного и емкостного сопротивлений определяют отношением: 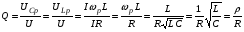 , ,3 Q1 > Q2 > Q3 I(ω) 1 2 ω ω0 Рис. 4.5 Iр 0.707Iр Δω называемой добротностью контура. Добротность определяет избирательные свойства контура. Чем больше добротность контура, тем более узкой будет резонансная кривая (рис. 4.5). Избирательность контура характеризуется полосой пропускания. Полоса пропускания – это диапазон частот, для которых ток ослабляется не более чем в 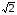 раз по отношению к максимальному значению раз по отношению к максимальному значению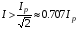 . .Ширина полосы пропускания равна 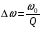 . .Порядок построения векторной диаграммы. 1. Задать масштабы тока mI[A/cм] и напряжения mU [B/cм]. 2. Вдоль действительной оси в выбранном масштабе тока отложить вектор тока 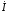 . .3. В масштабе напряжений отложить вектор активного напряжения 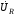 , совпадающий по фазе с током. , совпадающий по фазе с током.4. К концу вектора 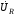 достроить вектор индуктивного напряжения достроить вектор индуктивного напряжения 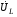 , опережающий ток на угол , опережающий ток на угол 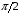 . .5. К концу вектора 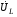 достроить вектор емкостного напряжения достроить вектор емкостного напряжения 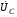 , отстающий от тока на угол , отстающий от тока на угол 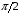 . .6. Соединить начало первого вектора с концом последнего, это будет вектор полного напряжения цепи. Порядок выполнения работы 1. В исходной схеме (рис.4.6) оставить элементы в соответствии с заданным вариантом 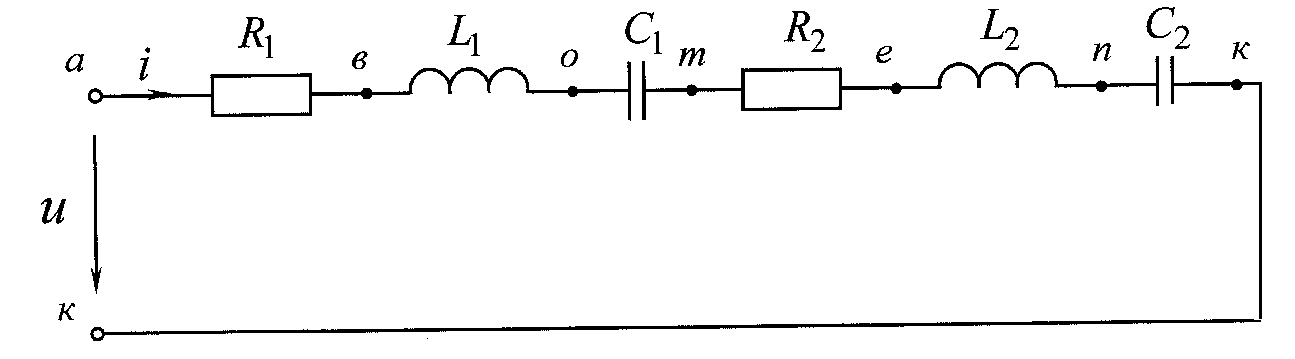 Рис. 4.6. 2. Для полученной схемы рассчитать параметры, указанные в задании. Принять частоту f=50 Гц. Проверить полученные результаты у преподавателя. 3. Собрать электрическую цепь, согласно полученному варианту задания и установить заданные параметры. 4. Записать в таблицу 4.1 заданные значения параметров цепи. Таблица 4.1.
5. Рассчитать резонансную частоту. 6. Измерить ток в цепи и напряжения на каждом элементе при значениях частоты: 50 Гц, 0,2 fрез, 0,4 fрез, 0,6 fрез, 0,8 fрез fрез, 1,2 fрез, 1,4 fрез, 1,6 fрез, 1,8 fрез. Результаты записать в таблицу 4.2. Таблица 4.2.
7. По результатам измерений построить частотные характеристики тока и напряжений. 8. Построить векторные диаграммы для трех режимов работы цепи: а) на любой частоте до резонанса; б) резонанс; в) на любой частоте после резонанса. 9. Из диаграмм определить величину напряжения на входе цепи и сравнить с заданным. Определить угол сдвига фаз между током и напряжением. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||