МУ к ЛР Электротехника ИБб. Методические указания по выполнению лабораторных работ для обучающихся по направлению 10. 03. 01 Информационная безопасность, профиль подготовки Комплексная защита объектов информатизации (в сфере техники и технологии). Иркутск. Ирниту, 2018. 40 с
 Скачать 1.05 Mb.
|
|
Контрольные вопросы 1. Что такое параллельный колебательный контур основного вида? Какой вид резонанса в нем происходит? Чему равны основные параметры (резонансная частота, входное сопротивление, резонансное сопротивление, характеристическое сопротивление, добротность) такого контура? 2. Что такое параллельный колебательный контур с разделенной индуктивностью? Какие виды резонанса в нем происходят? Для чего применяется такой контур? Чему равны основные параметры (резонансные частоты, входное сопротивление, резонансное сопротивление, характеристическое сопротивление, добротность) такого контура? Какие параметры контура зависят от коэффициента включения индуктивности, а какие не зависят? 3. Докажите, что добротность параллельного колебательного контура с разделенной индуктивностью равна добротности параллельного контура основного вида. 4. Почему для последовательного колебательного контура желателен источник энергии, близкий по своим характеристикам к идеальному источнику напряжения, а для параллельного - источник энергии, близкий по своим характеристикам к идеальному источнику тока? Лабораторная работа № 6 Исследование переходных процессов в цепи второго порядка при ее подключении к источнИку постоянного напряжения Цель работы: изучить характер переходных процессов, происходящих в разветвленной цепи второго порядка при ее подключении к источнику постоянного напряжения. Краткие теоретические сведения Рассмотрим цепь, изображенную на рис. 6.1. В момент времени t= 0 замыкают ключ S. Поскольку до коммутации цепь была разомкнута, то напряжение на конденсаторе и ток через катушку были равны нулю (нулевые начальные условия).  Рис. 6.1 Составим характеристическое уравнение цепи, для этого запишем комплексное сопротивление цепи относительно зажимов источника напряжения, а затем заменим множитель jω на p; числитель полученного выражения приравняем нулю: 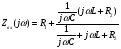 , ,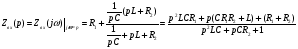 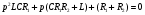Последнее выражение и есть характеристическое уравнение цепи. Вид переходного процесса зависит от типа корней характеристического уравнения. Поскольку в данном случае характеристическое уравнение представляет собой квадратное уравнение, то в зависимости от конкретных значений параметров элементов цепи (и, следовательно, коэффициентов уравнения) возможны следующие варианты: - уравнение имеет два различных вещественных корня; при этом соответствующие собственные функции (свободные составляющие p1, p2 токов или напряжений) имеют вид: 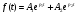 постоянные времени: 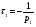 ;   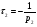; переходный процесс апериодический (монотонный) затухающий;- уравнение имеет два одинаковых вещественных корня p1 = p2; при этом соответствующие собственные функции (свободные составляющие токов или напряжений) имеют вид: 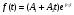 постоянная времен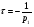и:  ; переходный процесс апериодический (монотонный) затухающий;- уравнение имеет пару комплексно-сопряженных корней 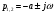 ; при этом соответствующие собственные функции (свободные составляющие токов или напряжений) имеют вид: п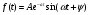остоянная времен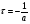и:  ; переходный процесс колебательный затухающий.В приведенных выражениях А1, А2, А, ψ - постоянные интегрирования, определяемые по начальным условиям. В любом случае значения вещественных корней или значение действительной части комплексно-сопряженных корней определяют время затухания переходного процесса; следует также учитывать, что для физически реализуемых цепей эти значения должны быть отрицательными (иначе процесс был бы не затухающим, а расходящимся). Дискриминант характеристического уравнения равен: 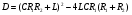 из этого выражения видно, что знак дискриминанта характеристического уравнения, а, следовательно, тип корней характеристического уравнения и характер переходного процесса, зависит от значений параметров всех пассивных элементов цепи. Причем знак дискриминанта может измениться даже при изменении значения параметра одного элемента цепи при неизменных значениях параметров остальных элементов. Описание измерительной установки Соберите схему измерительной установки в соответствии с заданным вариантом. Установка состоит из источника постоянной ЭДС (батареи), выключателя, двух резисторов, конденсатора и катушки. Для наблюдения переходных процессов к исследуемой схеме подключен осциллограф. Исходные параметры элементов указаны в задании. Порядок выполнения работы 1. Решить характеристическое уравнение цепи, учитывая значения полученных корней характеристического уравнения, определить характер переходного процесса и записать выражение, описывающее зависимость напряжения на конденсаторе от времени (численные значения постоянных интегрирования можно не рассчитывать). 2. Собрать схему измерительной установки в соответствии с заданным вариантом.. 3. Задать в программе режим анализа переходных процессов (параметр «Transient» в меню «Circuit - Analysis options») и покадровый режим работы осциллографа (флажок «Pause after each screen» в меню «Circuit - Analysis options»). 4. Установить на осциллографе время развертки таким образом, чтобы горизонтальный размер экрана примерно соответствовал времени переходного процесса (время переходного процесса условно принять равным 5τmax, где τmax - максимальная постоянная времени цепи). Усиление соответствующего канала на осциллографе необходимо установить так, чтобы осциллограмма процесса полностью умещалась на экране. Осциллограф следует переключитьв режим открытого входа (DC). 5. Включить схему при разомкнутом положении выключателя S. 6. Осуществить коммутацию цепи: для этого следует замкнуть ключ S; переключение производится нажатием клавиши [Пробел]. После коммутации следует нажать клавишу [F9]. 7. Зарисовать полученную осциллограмму переходного процесса, при этом необходимо указать время развертки и усиление используемого канала на осциллографе. 8. Повторить действия п.п. 1 - 7 для следующих значений емкости конденсатора: 600 нФ; 420 нФ, 100 нФ, 10 нФ. 9. Заполнить отчет. Отчет должен содержать титульный лист, цель работы, схему исследуемой цепи, расчеты (п. 1) и осциллограммы (п. 7) процесса при различных значениях емкости конденсатора, выводы. Контрольные вопросы 1. Какие переходные процессы возможны в цепях второго порядка при их подклю чении к источнику постоянной ЭДС? 2. Опишите способы составления характеристического уравнения электрической цепи. Сколько корней имеет характеристическое уравнение электрической цепи второго порядка? Как зависит характер переходного процесса от вида корней характеристического уравнения? 3. Объясните физический смысл корней характеристического уравнения электрической цепи второго порядка в случае, если эти корни вещественные? 4. Объясните физический смысл действительной и мнимой частей корней характеристического уравнения электрической цепи второго порядка в случае, если эти корни комплексно-сопряженные? 5. Изменится ли характер переходного процесса при изменении напряжения источника постоянной ЭДС? Почему? Список литературы 1. Атабеков Г. И. Основы теории цепей : учебник / Г. И. Атабеков, 2017. – 424 с. 2. Лессинг А. А. Теория электрических цепей : учебное пособие / А. А. Лессинг, 2012. - 239 с. 3. Ружников В. А. Основы теории цепей : учеб. пособие / В. А. Ружников, А. А. Лессинг, Н. В. Должикова, 2005. - 320 с. 4. Попов В. П. Теория электрических цепей в 2 ч. часть 1 [Электронный ресурс] : Учебник / Попов В.П., 2018. - 378 с. |