Методические указания по выполнению практического занятия 2 Раздел Комплексные числа Тема Тригонометрическая форма комплексного числа
 Скачать 401.73 Kb. Скачать 401.73 Kb.
|
|
Методические указания по выполнению практического занятия № 2 Раздел 1.Комплексные числа Тема 1.2. Тригонометрическая форма комплексного числа Название практической работы: Действия над комплексными числами в тригонометрической форме. Учебная цель: формирование умения выполнять действия над комплексными числами в тригонометрической форме. Норма времени: 1 час 30 минут Образовательные результаты, заявленные во ФГОС третьего поколения: Студент должен уметь: У.1 - Решать прикладные задачи в области профессиональной деятельности Ход работы Теоретические сведения к практической работе Модулем комплексного числа назовем длину отрезка 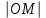 (или расстояние от начала координат до точки M), т.е. (или расстояние от начала координат до точки M), т.е. 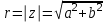 . . Аргументом комплексного числа ( 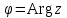 ) назовем угол, который вектор ) назовем угол, который вектор 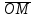 образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию 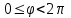 . Угол φ вычисляется по формулам . Угол φ вычисляется по формулам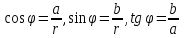 (1.1) (1.1)Из (1.1) следует, что 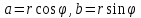 , тогда , тогда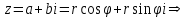 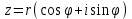 (1.2) (1.2)называется тригонометрической формой записи комплексного числа. Действия на  д комплексными числами в тригонометрической форме д комплексными числами в тригонометрической формеПример 1. Найти модуль и аргумент комплексного числа 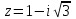 . .Решение. По определению 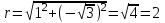 . Для определения аргумента воспользуемся формулой: . Для определения аргумента воспользуемся формулой: 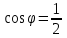 . Угол расположен в IV четверти. Получаем, что . Угол расположен в IV четверти. Получаем, что 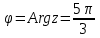 . .Пример 2. Представить число z =1+iв тригонометрической форме.  Пример 3. Записать комплексное число 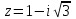 в тригонометрической форме. в тригонометрической форме.По определению 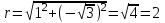 . Для определения аргумента воспользуемся формулой: . Для определения аргумента воспользуемся формулой: 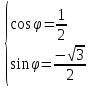 . Получаем, что . Получаем, что 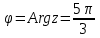 . Тригонометрическая форма заданного комплексного числа имеет вид: . Тригонометрическая форма заданного комплексного числа имеет вид: 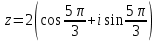 . .Пример 4.Записать число z=2(cos 3300 + isin 3300) в алгебраической форме. Решение. Т.к. 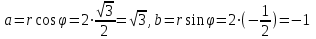 , то , то z=2(cos 3300 + i sin 3300) 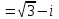 Пример 5.Даны комплексные числаz1=12(cos 2250+isin2250) и z2=3/2(cos 750 + i sin 750). Найдите z1*z2 и z1/z2. Решение: Применяя правила умножения и деления комплексных чисел, имеем: z1*z2=12*(3/2)(cos(2250+750)+isin(2250+750))=18(cos3000+ sin3000)=18( 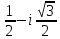 )=9-9i )=9-9i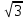 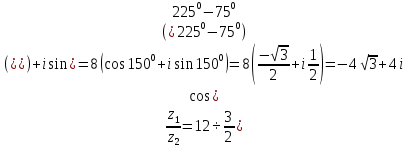 Пример 6. Дано 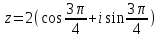 . Вычислить z4, . Вычислить z4, 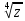 Решение. 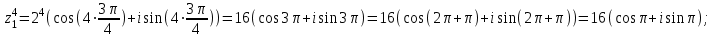 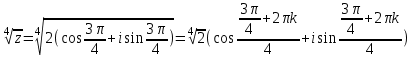 , где k = 0, 1, 2, 3. , где k = 0, 1, 2, 3.При k = 0, 1, 2, 3 получим 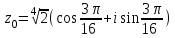 ; ;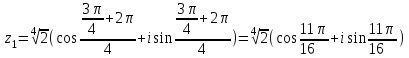 ; ; 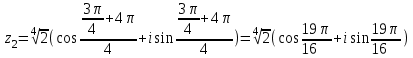 ; ;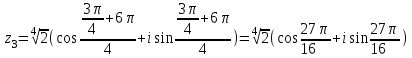 Вопросы для самоконтроля Дайте определение модуля и аргумента комплексного числа. Каков их геометрический смысл? Напишите тригонометрическую форму комплексного числа. Как умножить и разделить два комплексных числа в тригонометрической форме? По какой формуле находится корень n-й степени из комплексного числа в тригонометрической форме? Обеспеченность занятия (средства обучения): методические указания по выполнению практического занятия; рабочая тетрадь, справочник по математике ручка, калькулятор Содержание практической работы 1 вариант 2 вариант 3 вариант 4 вариант Представить в тригонометрической форме число Ƶ Ƶ=1+ 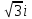 Ƶ=2+2i Ƶ=5-5i Ƶ= Ƶ=2+2i Ƶ=5-5i Ƶ= 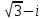 Представьте в алгебраической форме число Ƶ Ƶ=2 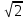 ( (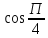 +i +i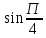 ) Ƶ=4( ) Ƶ=4(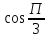 +i +i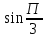 ) Ƶ=3( ) Ƶ=3(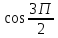 +i +i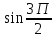 ) Ƶ=4( ) Ƶ=4(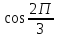 +i +i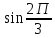 ) )Выполните действие Ƶ1*Ƶ2 Ƶ1=3 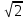 ( (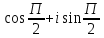 ) ) 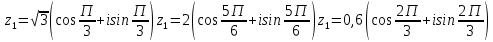  Ƶ2= 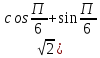 ) ) 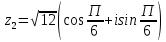 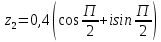 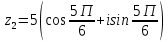 Найдите частное комплексных чисел: 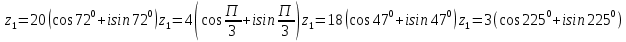 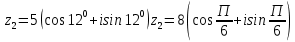 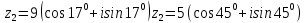 Вычислите: а). (2(cos240 + i sin240)5 а) ( 2(сos500 + i sin500))6 а) ( 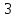 ( (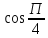 +i +i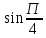 ))4 а) (2 ))4 а) (2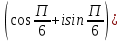 4 4б). 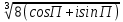 б) б)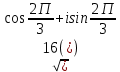 б) б)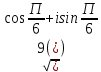 б) б)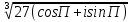
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
