паскаль. Методическое пособие для учителя Томск2006 Графика Принципы работы с видеотерминалом в системе Turbo Pascal 0

• Название: Методическое пособие для учителя Томск2006 Графика Принципы работы с видеотерминалом в системе Turbo Pascal 0
• Анкор: паскаль.doc
• Дата: 13.08.2018
• Размер: 0.75 Mb.
• Имя файла: паскаль.doc
• Тип: Методическое пособие; #22892
• страница: 6 из 7

Фрактальный морфинг

Если есть описание еще одного фрактала в формате IFS, например листа папоротника, можно произвести морфинг (непрерывное преобразование одного в другой). Приведем фрагмент программы, задающий лист папоротника в формате IFS в пакете FRACTINT (см. рис. 7.).
Рис. 7. Изображение листа папоротника, полученное с помощью IFS

Fern     {
    0        0           0       .16     0      0         .01
   .85     .04      -.04     .85     0      1.6     .85
   .2      -.26       .23     .22     0      1.6     .07
  -.15     .28       .26     .24     0      .44     .07
}

    Для осуществления морфинга достаточно линейно интерполировать элементы одной матрицы в те же элементы другой и строить фракталы для каждого из промежуточных состояний. Чтобы получить лучший визуальный эффект, нужно продумать положение строк в матрицах. При выводе одного фрактала этот факт не играет роли. При построении разных фракталов с использованием IFS можно отметить, что они все имеют разные размеры, и поэтому нуждаются в масштабировании (cм. приложение). На рис. 8 приведен пример фрактального морфинга.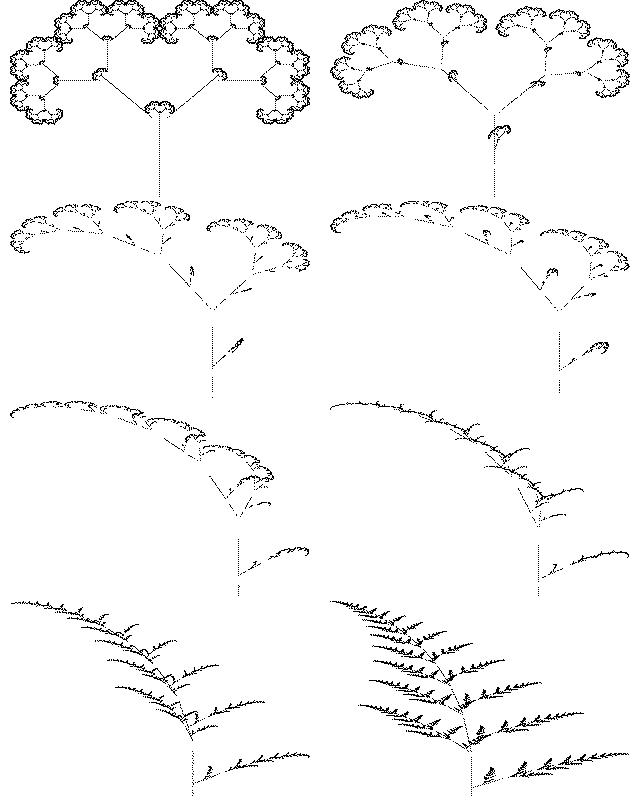



Рис. 8. Пример фрактального морфинга "дерева" в "лист папоротника"

Фрактальное сжатие изображений

    При помощи фракталов можно сжимать произвольные изображения с некоторой потерей качества, аналогично сжатию JPEG. Правда, фрактальное сжатие дает лучшие результаты. Методы компрессии, основанные на RLE, Huffman или LZW, не учитывают природы сжимаемых данных и поэтому дают неудовлетворительные результаты при обработке изображений. При фрактальном сжатии изображение переводится в формат IFS, который значительно экономнее, чем просто BITMAP или LZW.
    Сжатие JPEG основано на дискретном синусно-косинусном преобразовании (дискретное преобразование Фурье), которое переводит изображение в амплитудно-фазовую форму. Искажения в области высоких частот не сильно влияют на качество исходных изображений, поэтому их частично отбрасывают, а частично фильтруют НЧ-фильтром с последующим сжатием при помощи RLE и тому подобных методов. Поэтому метод JPEG дает плохие результаты на изображениях, содержащих тонкие линии (текст или чертежи). Для того, чтобы получить прямоугольный сигнал, а тонкая лини именно таким сигналом и является, необходимо использовать область высоких частот, которые в нашем случае фильтруются, подвергаясь при этом искажению.
    Основная проблема фрактального сжати - это то, что компрессия-декомпресси производится быстро и однозначно, в то время как прямая процедура требует от машины больших интеллектуальных возможностей. Правильное сжатие - это серьезная задача, решение которой можно найти в науке о распозновании образов.
    Сжатие происходит следующим образом. Изображение разбивается на части множеством R и покрывается множеством D. Причем элементы множества D больше по площади, чем R. Для каждого элемента Ri перебираются все элементы множества D и строится аффинное преобразование R(i) -> D(j). Из всех преобразований выбирается одно, которое происходит с наименьшей погрешностью. Афинное преобразование выполняется по трем координатам - X, Y, Цвет. Приведем это преобразование:

x      a b 0      x       e
y  =  c d 0  *  y  +  f
c      0 0 s      c       o

a, b, c, d, e, f - коэффициенты преобразовани на плоскости.
s - контрастность.
o - яркость.

    Остальные коэффициенты равны 0, потому что нет необходимости связывать изменение цвета с преобразованием координат. От числа преобразований, то есть мощности множества R, зависит степень компрессии, ведь на каждое преобразование требуется 8 чисел. Множество таких преобразований и составляет систему итерирующих функций .
    Разбиение на R и покрытие D являютс самой сложной частью алгоритма. В простейшем случае это делается так: изображение разбивают регулярной сеткой R(i) по 8 x 8 пикселов. Для каждого R(i) перебирают все возможные D(j) по 16 x 16 (причем есть 8 вариантов для каждого квадрата - 4 поворота на 90о и зеркальная симметрия). Для каждого R(i) вводят свое лучшее преобразование, а потом ищут минимальное покрытие исходного изображения из имеющихся D(j). Оставляют только те преобразования, которые нужны для минимального покрытия.
    Декомпрессия производится следующим образом. Выбирают начальное изображение, из которого будут строить оригинал. Самое удивительное, что от выбора начального изображения меняется только скорость стабилизации изображения, то есть врем декомпрессии. В настоящее время мне не известны способы оптимального выбора инициатора, поэтому заполним его случайными числами или константой. К каждому элементу множества R (то есть квадрату 8x8 из инициатора) применяют случайно выбранное аффинное преобразование из имеющейся системы функций. В результате такого действия элементы изображения копируются в другие части экрана с изменением ориентации, яркости и контраста. После того, как все R(i) перебраны, начинаем все сначала. По теореме о системе сжимающих аффинных преобразований, описанной в статье [7], изображение будет стремиться к стабильности. Обычно достаточно 10.. 20 итераций.
    При компрессии можно не сохранять оригинальные размеры изображения, достаточно просто запомнить их соотношение. А при декомпрессии - задавать те размеры, которые нам больше подходят. Такая возможность позволяет решить задачу экстраполяции исходного изображения. При установке новых размеров, превышающих старые, в новое изображение добавятся элементы, подобные другим элементам изображения. И если обрабатывается природный объект (например гранитный камень), то подмена не будет заметна.