паскаль. Методическое пособие для учителя Томск2006 Графика Принципы работы с видеотерминалом в системе Turbo Pascal 0

• Название: Методическое пособие для учителя Томск2006 Графика Принципы работы с видеотерминалом в системе Turbo Pascal 0
• Анкор: паскаль.doc
• Дата: 13.08.2018
• Размер: 0.75 Mb.
• Имя файла: паскаль.doc
• Тип: Методическое пособие; #22892
• страница: 2 из 7

Графический режим

Переход в графический режим.

Графические изображения в среде Turbo Pascal формируются из ряда светящихся точек – пикселей. Любой пиксель задается парой координат. Начало координат – точка (0,0) – левый верхний угол экрана. Для различных графических режимов работы координатные сетки могут быть разными.  Средства управления экраном в графическом режиме находятся в модуле GRAPH. Для того чтобы работа в графическом режиме была корректна, необходимо проверить, есть ли файл 'graph.tpu' в том каталоге, на который указывает опция Options\Directories\Unit Directories главного меню среды Turbo Pascal.  После загрузки среды TP видеотерминал находится по умолчанию в текстовом режиме. Для того, что перейти в графический режим, необходимо предусмотреть в программе вызов графического драйвера. Для этой цели служит процедура:  

initgraph(<тип>,<режим>,<адрес>);  

где    <тип> определяет тип драйвера;
   <режим> задает режим работы видеоадаптера;
   <адрес> определяет адрес директории, в которой находится искомая программа-драйвер (программа 'egavga.bgi', обычно расположена в каталоге BGI папки TP или BP).

Если тип используемого в компьютере адаптера неизвестен, то можно обратиться к процедуре initgraph с требованием автоматического определения типа адаптера. Для этого необходимо в качестве первого параметра процедуры использовать 0 или константу Detect.  Для завершения работы адаптера в графическом режиме и перевода его в текстовый режим служит процедура  

closegraph;  

Пример.  

Program grafika;
   uses graph;
   var gd, gm, errorcode: integer;
      ga:string;
Begin
   gd:=detect;
   ga:='d:\bp\bgi';
   initgraph(gd, gm, ga);
   errorcode:=graphresult;
   if errorcode <> 0 then
   begin
   write(errorcode);
   halt(1);
   end;
   readln;
   closegraph;
End.

Принципы управления палитрой

Палитра – это совокупность одновременно доступных цветов.  Номер цвета в палитре – это его порядковый номер от 0 до 15; код цвета – это число типа shortint, определяющее выбранный цвет и лежащее в диапазоне от 0 до 63. Выбрать из палитры цвет, который будет использоваться для вывода изображения, позволяет процедура:  

setcolor(<номер цвета в палитре>);  

Максимально допустимый номер цвета, который может быть передан процедуре setcolor, определяется значением функции:  

getmaxcolor;  

Цвет фона можно определить с помощью процедуры:  

setbkcolor(<номер цвета в палитре>);  

Работа с точками и графическими примитивами

В модуле graph содержится достаточно большое количество процедур и функций, осуществляющих работу с точками и графическими примитивами. Рассмотрим некоторые из них.  

1. 
   процедура putpixel(X,Y,C);
   

 выводит на экран точку цветом C с координатами (X,Y);  

2. 
   процедура line(X1,Y1,X2,Y2);  
   

вычерчивает отрезок текущего цвета и типа с концами в точках (X1,Y1), (X2,Y2).  

Тип линии можно установить с помощью процедуры  

setlinestyle(<вид>,<образ>,<толщина>); (см. контекстную помощь)

3. 
   процедура lineto(X,Y);
   

 вычерчивает отрезок текущего типа и цвета от текущей позиции курсора до точки с координатами (X,Y).  

Получить информацию о текущем положении графического курсора можно при помощи функций getx и gety (см. систему помощи).  

Переместить графический курсор в точку с заданными координатами можно при помощи процедуры moveto(X,Y);  

4. 
   процедура rectangle(X1,Y1,X2,X2);  
   

вычерчивает прямоугольник с диагональными вершинами (X1,Y1) и (X2,Y2) линией текущего типа и цвета

5. 
   процедура bar(X1,Y1,X2,Y2);  
   

аналогична процедуре rectangle, но прямоугольник заполняется текущим узором

Установить тип и цвет узора можно при помощи процедуры  

setfillstyle(<тип узора – число от 1 до 12>,<цвет>); (см. систему помощи)  

6. 
   процедура bar3d(X1,Y1,X2,Y2,Z,T);  
   

строит параллелепипед текущего цвета с закрашенной текущим узором передней гранью. Параметр Z определяет глубину параллелепипеда, T – параметр логического типа, который определяет, прорисовывать (true) или нет (false) верхнюю грань

7. 
   процедура circle(X,Y,R);  
   

вычерчивает окружность текущего цвета с центром в точке (X,Y) и радиусом R.  

8. 
   процедура ellipse(X,Y,A,B,XR,YR);  
   

вычерчивает эллипс (или эллиптическую дугу) текущего цвета с центром в точке (X,Y). Параметры A,B задают значения в радианах начального и конечного углов, ограничивающих дугу; XR и YR – большой и малый радиусы.  

9. 
   процедура arc(X,Y,A,B,R);  
   

вычерчивает дугу окружности радиуса R с центром в точке (X,Y) из угла A в угол B. 10) процедура fillellipse(X,Y,XR,YR);

 вычерчивает эллипс текущего цвета, заполненный текущим узором

11. 
    процедура pieslice(X,Y,A,B,R);  
    

вычерчивает сектор круга текущего цвета, заполненный текущим узором.  

11. 
    процедура sector(X,Y,A,B,XR,YR);  
    

вычерчивает сектор эллипса текущего цвета и заполняет его текущим узором

Вывод текстовых сообщений в графическом режиме

Процедуры write и writeln могут быть использованы только в текстовом режиме, т.к. именно в этом режиме экран дисплея рассматривается как консольное устройство CON. В графическом режиме для вывода на экран дисплея текстовых сообщений необходимо использовать одну из двух стандартных процедур модуля graph:  

1)outtext (<строка>)  

выражение строкового типа <строка> выводится на экран, начиная с текущей позиции графического курсора;  

2)outtextxy(X,Y,<строка>)

 выражение <строка> выводится на экран, начиная с заданных координат (X,Y).

Установить вид выводимых на экран символов позволяет процедура  

3)settextstyle(<шрифт>,<направление>,<размер>);  

Шрифт выводимых символов задается числом из диапазона 0..10. Шрифты с 1 по 10 – векторные, с которыми просто проводятся операции масштабирования. Для русского алфавита может быть использован только шрифт 0. Направление выводимого текста задается значением 0 – горизонтальное или 1 – вертикальное.

Размер символов сообщения определяется коэффициентом увеличения символа.  В случае использования векторных шрифтов размер выводимых символов можно регулировать с помощью процедуры:  

4)setusercharsize(MX,DX,MY,DY),  

которая изменяет ширину и высоту символов активного шрифта. Параметры MX,DX задают коэффициент изменения ширины (как отношение MX/DX), а параметры MY,DY определяют высоту символа при выводе. Стандартный размер символов, по отношению к которому осуществляется масштабирование, устанавливается процедурой 3).

В языке TURBO Pascal имеется значительное количество графических процедур и

функций. Нам понадобятся лишь некоторые из них. Для того чтобы компилятор

"узнавал" их названия, мы должны после заголовка программы разместить строчку

следующего вида:

uses Graph; (что в переводе на русский означает "используется графика").

До сих пор во время нашей работы за компьютером экран всегда находился в

текстовом режиме, поэтому на экране можно было видеть только лишь символы

(правда, включая такие изыски, как так называемые "символы псевдографики").

Для рисования прямых, окружностей и пр. необходимо перевести экран в графический

режим. Для включения графического режима используется процедура InitGraph.

Простейшая программа может иметь вид:

Пример 1.

PROGRAM Primer_1;

uses Graph;

var Gd,Gm: Integer;

BEGIN

Gd:=VGA; { Графический адаптер - VGA }

Gm:=VGAHi; {Графический режим VGAHi (640x480)}

InitGraph (Gd,Gm,'..\bgi'); {Включить графический режим }

If GraphResult=grOk

then {Если режим включился успешно}

{ Нарисовать отрезок прямой}

Line (0,0,639,479); ReadLn

END.

Мы видим, что у процедуры InitGraph три параметра. В качестве первых двух

фактических параметров должны стоять имена целых (integer) переменных. Не будем

вдаваться в подробности, почему это так; вместо этого выясним их предназначение.

Первый параметр является кодом графического адаптера (т.е. электронной схемы,

управляющей выводом информации на экран). (Дело в том, что на IBM-совместимых

компьютерах применяется ряд стандартных графических адаптеров, носящих названия

CGA, EGA, VGA.)

По нашей программе можно догадаться, что в используемых нами компьютерах

используется адаптер VGA, и компилятор сам "узнает" слово VGA и заменит его на

нужное целое число (на самом деле равное 9, но мы этого можем и не запоминать).

Каждый графический адаптер позволяет использовать несколько графических режимов, отличающихся количеством цветов и разрешающей способностью (в дальнейшем мы узнаем, что это такое). И второй из параметров как раз предназначен для того, чтобы указать, какой из графических режимов следует включить. Пока что мы

ограничимся лишь одним графическим режимом VGAHi.

Третий параметр является строкой, содержащей путь к файлу, который называется

EGAVGA.BGI. В этом файле содержится драйвер (такая специальная программа),

необходимый для работы с адаптерами EGA и VGA. И, как легко увидеть из нашего

примера, файл этот находится в подкаталоге TPBGI.

Все вышеизложенное необходимо знать каждому грамотному пользователю

IBM-совместимых компьютеров. Однако в нашей лабораторной работе достаточно

использовать конструкцию, использованную в первом примере, для включения

графического режима. (И не страшно, если в ней не все понятно.)

Для того чтобы мы могли что-либо нарисовать на экране, нам нужно уметь задавать

положение на экране того, что мы рисуем. Для этого с экраном связывается система

координат следующего вида:

(0,0) X

+ --------------------------------------------->

|

|

|

Y|
Каждая точка на экране на самом деле представляет собой очень маленький

прямоугольник (и поскольку это не совсем точка, то иногда используют специальный

термин - "пиксел"). Количество точек (пикселов), умещающихся на экране по

вертикали и горизонтали, называют разрешающей способностью. Разрешающая

способность экрана в режиме VGAHi - 640x480. Это означает, что по горизонтали на

экране умещается 640 точек, а по вертикали - 480.

Точка в левом верхнем углу экрана имеет координаты (0,0). Координата X любой

точки экрана лежит в пределах от 0 до 639, а координата Y - в пределах от 0 до

479. Как Вы уже догадались, процедура Line (x1,y1,x2,y2) рисует на экране прямую,

соединяющую точки (x1,y1) и (x2,y2).


Пример 2.

Изобразить на экране прямоугольный треугольник с вершинами (320, 10),

(120,210), (520,210).

PROGRAM Primer_2;

uses Graph;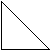

var Gd,Gm: Integer;

BEGIN

Gd:=VGA; Gm:=VGAHi; InitGraph (Gd,Gm,'..\bgi');

If GraphResult=grOk

then begin

Line (120,210,520,210); {Горизонтальный отрезок}

Line (120,210,320,10); {Левый катет }

Line (320,10,520,210); {Правый катет }

ReadLn

end; end.

Довольно обидно работать на цветном мониторе только с черно-белыми изображениями. Для задания цвета рисования прямых, окружностей, точек и пр. используется процедура SetColor. В качестве единственного ее параметра нужно указать целое число, являющееся кодом цвета. Цвета кодируются в соответствии со следующей кодовой таблицей:

Black=0-черныйDarkGray=8-темно-серый

Blue=1-синийLightBlue=9-голубо

Green=2-зеленыйLightGreen=10- светло-зеленый

Cyan=3-цвет морской волныLightCyan=11-светло-циановый

Red=4-красныйLightRed=12-розовый

Magenta=5-сиреневыйLightMagenta=13-светлосиреневый

Brown=6-коричневыйYellow=14- желтый

LightGray=7-светло-серыйWhite=15-белый

Если Вы хорошо знаете, английский язык, то Вам будет удобнее использовать не числа, а соответствующие им идентификаторы; если же Вы английский знаете плохо, то все равно полезнее запомнить английские названия цветов, чем запоминать числа, кодирующие цвета.

Пример 3.

Изобразить тот же треугольник, что и в предыдущем примере, но сделать стороны треугольника разноцветным.

PROGRAM Primer_3;

uses Graph;

var Gd,Gm: Integer;

BEGIN

Gd:=VGA; Gm:=VGAHi; InitGraph (Gd,Gm,'..\bgi');

If GraphResult=grOk

then begin

SetColor (LightMagenta); { Цвет - светло-сиреневый }

Line (120,210,520,210); {Горизонтальный отрезок }

SetColor (LightCyan); {Цвет - светло-циановый}

Line (120,210,320,10); {Левый катет }

Set Color (Green); { Цвет - зеленый }

Line (320,10,520,210); {Правый катет }

ReadLn

end

END.

Пример 4. Разноцветные лучи.

PROGRAM Primer_4;

uses Graph;

const CenterX=320;

CenterY=240;

Radius=200;

var Gd,Gm: Integer;

i : Integer;

dx,dy: Integer;

BEGIN

Gd:=VGA; Gm:=VGAHi; InitGraph (Gd,Gm,'..\bgi');

If GraphResult=grOk

then begin

For i:=0 to 160 do

begin

dx:=Round (Radius*sin(i*pi/80));

dy:=Round (Radius*cos(i*pi/80));

SetColor (i MOD 16);

Line(CenterX,CenterY,CenterX+dx,CenterY+dy)

end;

ReadLn

End END.

Пример 5 . Концентрические окружности.

Для рисования окружностей используется процедура Circle с тремя целочисленными

параметрами, задающими координаты центра окружности и радиус.

PROGRAM Primer_5;

uses Graph;

const CenterX=320;

CenterY=240;

var Gd,Gm: Integer;

i : Integer;

BEGIN

Gd:=VGA; Gm:=VGAHi; InitGraph (Gd,Gm,'..\bgi');

If GraphResult=grOk

then begin

For i:=0 to 23 do

Circle (CenterX,CenterY,i*10);

ReadLn

end

END.

Пример 6. Разноцветные концентрические окружности.

Для закраски замкнутой области используется процедура FloodFill, три

целочисленных параметра, которой задают начальную точку закраски и код цвета ограничивающей область линии. Цвет, которым будет производиться закраска, ничего общего не имеет с цветом, задаваемым процедурой SetColor. Цвет закраски задается вторым параметром процедуры SetFillStyle. Первый параметр этой процедуры (задающий узор для закраски) на первых порах будем задавать равным единице (что соответствует сплошной закраске).

PROGRAM Primer_6;

uses Graph;

const CX=320;

CY=240;

var Gd,Gm: Integer;

i : Integer;

BEGIN

Gd:=VGA; Gm:=VGAHi; InitGraph (Gd,Gm,'..\bgi');

If GraphResult=grOk

then begin

For i:=0 to 23 do

Circle (CX,CY,i*10);

For i:=0 to 23 do

begin

SetFillStyle (1,i MOD 16);

{ Закрашивать до границы белого цвета}

FloodFill (CX,CY+i*10-5,White)

end;

Readln

end

END.

Пример 7.

PROGRAM Primer_7;

uses Graph;

var grDriver: Integer;

grMode : Integer;

i,x,y : Integer;

PROCEDURE Rect (x,y,x1,y1: Integer);

{Рисует прямоугольник, у которого левый

нижний угол}

{ имеет координаты (x,y), а правый верхний - (x1,y1)}

BEGIN

Line (x,y,x,y1); {Левая сторона}

Line (x1,y,x1,y1); {Правая сторона}

Line (x,y1,x1,y1); {Верхняя сторона}

Line (x,y,x1,y) {Нижняя сторона}

END;

BEGIN

GrDriver:=VGA; GrMode:=VGAHi;

InitGraph (grDriver,grMode,'..\bgi');

If GraphResult=grOk

then begin

For i:=1 to 15 do

begin

x:=i*30; y:=i*25; SetColor (i);

Rect (x,y,x+50,y+60)

end;

ReadLn

End: end.

Рисование прямоугольников - часто встречающаяся проблема, и поэтому

неудивительно, что существует стандартная процедура, работающая так же, как и созданная нами ниже процедура Rect. Она называется Rectangle.

Пример 8.

Для рисования "заполненных" прямоугольников используется процедура Bar. Так же, как и для процедуры Rectangle, мы должны указать четыре числа - координаты двух противоположных углов прямоугольника. (Для процедуры Bar цвет задается не с помощью SetColor, а с помощью SetFillStyle!).

PROGRAM Primer_8;

uses Graph;

const Step=35;

var grDriver: Integer;

grMode : Integer;

i,x,y : Integer;

PROCEDURE Square (x,y: Integer);

{ Рисует цветастый квадрат, центр которого }

{ имеет координаты (x,y)}

var i,d: Integer;

BEGIN

For i:=15 downto 0 do

begin

SetFillStyle (SolidFill,i); d:=i*3+2;

Bar (x-d,y-d,x+d,y+d)

end

END;

BEGIN

GrDriver:=VGA; grMode:=VGAHi;

InitGraph (grDriver,grMode,'..\bgi');

If GraphResult=grOk

then begin

For i:=0 to 10 do

{ На "побочной" диагонали - 11 точек }

begin

x:=50+i*Step; y:=50+(10-i)*Step;

SetColor(i); Square(x,y)

end;

ReadLn

end

END.

При рисовании сложных изображений, содержащих много отрезков, возникает довольно противная проблема - вычислять координаты всех точек. Если использовать процедуру LineRel, то достаточно указывать смещения по обеим координатам относительно текущей точки.

Для относительного перемещения без рисования используется процедура MoveRel Для задания начальных значений координат текущей точкииспользуется процедура MoveTo

Пример 9. Квадратная спираль.

PROGRAM Primer_9;

uses Graph;

const CenterX=320;

CenterY=240;

d=12;

var grDriver: Integer;

grMode : Integer;

i,L : Integer;

PROCEDURE Vitok (L,dL: Integer);

{ Начиная от текущей точки, рисует виток спирали}

{ из четырех отрезков увеличивающейся длины}

{ L - длина первого отрезка}

{ dL - приращение длины для каждого из следующих отрезков }

BEGIN

LineRel (L,0); { Сдвинуться вправо }

LineRel (0,-(L+dL)); { Сдвинуться вверх }

LineRel (-(L+2*dL),0); { Сдвинуться влево }

LineRel (0,L+3*dL); { Сдвинуться вниз }

END;

BEGIN

grDriver:=VGA; grMode:=VGAHi;

InitGraph (grDriver,grMode,'..\bgi');

If GraphResult=grOk

then begin

{ Сделать текущей точкой центр экрана }

MoveTo (CenterX,CenterY);

L:=1; { Начальная длина отрезка }

For i:=1 to 10 do { 10 витков спирали }

begin Vitok (L,d); L:=L+4*d end;

ReadLn

end

END.

Пример 10. Небольшой городок.

PROGRAM Domiki;

uses Graph;

var grDriver: Integer;

grMode : Integer;

i,j : Integer;

PROCEDURE Domik (x,y: Integer);

{ Рисует домик, у которого левый нижний угол }

{ имеет координаты (x,y)}

const dx=60; { Ширина фасада }

dy=40; { Высота фасада }

dx2=dx DIV 2;

dy2=dy DIV 2;

wx=16; { Ширина окна }

wy=22; { Высота окна }

wx2=wx DIV 2;

wy2=wy DIV 2;

BEGIN

Rectangle (x,y,x+dx,y-dy); MoveTo (x,y-dy);

Linerel (dx2,-dx2); { Левый скат крыши }

Linerel (dx2,dx2); { Левый скат крыши }

Rectangle (x+dx2-wx2,y-dy2-wy2,x+dx2+wx2,y-dy2+wy2); { Окно }

MoveTo (x+dx2,y-dy2); { Центр фасада (и окна) }

LineRel (0,wy2); { Вертикальная часть рамы окна }

MoveTo (x+dx2-wx2,y-dy2); { Центр левой части рамы окна }

LineRel (wx,0); { Горизонтальная часть рамы окна }

SetFillStyle (SolidFill,Red);

FloodFill (x+1,y-1,White);

SetFillStyle (SolidFill,Blue);

FloodFill (x+dx2,y-dy-1,White)

END;

BEGIN

grDriver:=VGA; grMode:=VGAHi;

InitGraph (grDriver,grMode,'..\bgi');

If GraphResult=grOk

then begin

For i:=1 to 6 do

For j:=1 to 5 do

Domik (i*80,j*80);

ReadLn

end

END.

Если Вас интересуют другие графические процедуры или функции, то Вам следует обратиться к системе "помощи" (Help). Для этого в меню Help выберите пункт Standard units. Среди всего прочего Вы увидите список названий стандартных модулей (неважно, что вы не знаете, что это такое). Если установить курсор на слово Graph (этого можно достигнуть и с помощью клавиши Tab) и нажать Enter, то на экране появится общая информация о модуле Graph. Для продолжения нам предлагается два выбора:

Go to GRAPH.TPU Functions and Procedures

Go to GRAPH.TPU Constants and Types

Если выбрать пункт "Перейти к константам и типам GRAPH.TPU", то Вы сможете добраться до такой полезной информации, как названия графических режимов и их разрешение, названия цветов, названия стилей закраски и т.п. На случай, если Вам захочется там что-нибудь поискать, приведем перевод названий некоторых пунктов соответствующего меню:

Color Constants Цветовые константы

Fill Pattern Constants Константы для образцов закраски

Graphics Drivers Графические драйверы

Graphics Modes for Each Driver Графические режимы для каждого драйвера

Выбрав же пункт "Перейти к процедурам и функциям GRAPH.TPU", мы увидим внушительный список названий графических процедур и функций. Если поместить курсор на название приглянувшейся Вам процедуры (или функции), и нажать "перевод строки", то Вы увидите краткое описание этой процедуры (функции), и в конце - предложение посмотреть пример. (Если, скажем, Вы читаете информацию о процедуре Ellipse, то в самом конце Вы увидите слова

Sample Code:

Ellipse.PAS

Если установить курсор на слова Ellipse.PAS и нажать "перевод строки", то на экране Вы увидите текст программы, иллюстрирующий применение этой процедуры). Эта информация может пригодиться даже тем, кто не знает ни одного английского слова - Вы увидите, сколько у процедуры параметров и какие у этих параметров типы; Вы можете обычным образом (клавишами управления курсором при нажатой клавише Shift) отметить текст примера, скопировать в пустое окно и запустить.

Пример 11. Изобразить график функции y=cos(x).

При изображении графика функции необходимо иметь ввиду, что начало графических координат находится в левом верхнем углу экрана и что графические координаты принимают целые неотрицательные значения в диапазоне (0,maxx) и (0,maxy). Значения maxx и maxy для каждого режима можно определить, используя соответствующие функции. Таким образом, для получения "хорошего" графика необходимо выполнить поворот и масштабирование. Пусть, xmax - максимальное значение по оси x; ymax - максимальное значение по оси y;

(x0,y0) - графические координаты центра - точки (0,0);

(xg,yg) - графические координаты точки (x,y);

mx - масштаб по оси x, т.е. величина Abs((xg-x0)/x);

my - масштаб по оси y, т.е. величина Abs((yg-y0)/y).

Графические координаты точки (x,y): xg=x0+mx*x; yg=y0-my*f(x).

PROGRAM Primer_11;

Uses Graph;

var x,y,a,b,h : Real;

x0,y0,xg,yg,xmax,ymax,mx,my,grd,grm,c: Integer;

BEGIN

WriteLn ('Введите координаты центра: '); ReadLn (x0,y0);

WriteLn ('Введите масштаб по x и y: '); ReadLn (mx,my);

WriteLn ('Введите область задания функции по x и шаг: ');

ReadLn (a,b,h); WriteLn ('Введите цвет изображения: ');

ReadLn (c); grd:=0; grm:=0; InitGraph (grd,grm,'');

c:=getcolor; xmax:=getmaxx; ymax:=getmaxy;

Line (10,y0,xmax-10,y0); { Ось OX }

Line (x0,10,x0,ymax-10); { Ось OY }

x:=a;

While x<=b do

begin

xg:=x0+Trunc(mx*x); yg:=y0-Trunc(my*f(x));

If (xg>=0) AND (xg<=xmax) AND (yg>=0) AND (yg<=ymax)

then putpixel (xg,yg,c);

x:=x+h

end;

ReadLn;

closegraph

END.

Пример 12. Изобразить движение шарика по синусоиде.

Движение реализуется с помощью процедур GetImage и PutImage. Процедура GetImage запоминает образ изображаемого объекта и образ области экрана такого же размера, закрашенной цветом фона. Процедура PutImage на каждом шаге последовательно заменяет старое изображение цветом фона и создает изображение на новом месте.

PROGRAM Primer_12;

{ Программа движения шарика со следом по синусоиде }

uses Graph;

var p1,p2: Pointer;

{ p1 - указатель на образ "следа",

p2 - указатель на образ шарика }

grm,grd,x,y,x1,y1: Integer;

size,c : Word;

BEGIN

grd:=0; InitGraph (grd,grm,'D:\Tp\Bgi');

{ Инициализация графического режима с автоматическим

определением подходящего драйвера }

c:=GetColor; { c - цвет изображения }

x1:=0;y1:=90; { x1,y1 - начальные координаты шарика }

PutPixel (0,y1+5,c); { Изображение "следа" }

size:=ImageSize(0,0,10,10); GetMem (p1,size);

{ size - количество байтов для изображения квадрата 11x11 }

GetImage (0,y1,10,y1+10,p1^);

{ p1 указывает на область памяти с изображением следа }

SetFillStyle (11,c); { Устанавливается тип и цвет закраски }

Circle (x1+5,y1+5,5); { Окружность с центром в (x1,y1) }

FloodFill (x1+5,y1+5,c); { Закраска окружности }

GetMem (p2,size); GetImage (x1,y1,x1+10,y1+10,p2^);

{ p2 указывает на область памяти с изображением шарика }

For x:=1 to 300 do

begin

y:=Trunc (40*sin(0.1*x)+90);

{ x,y - графические координаты нового положения шарика }

PutImage (x1,y1,p1^,0); { На месте шарика изображается след }

PutImage (x,y,p2^,0); { Шарик изображается на новом месте }

x1:=x; y1:=y { Запоминаются новые координаты шарика }

end;

ReadLn; Closegraph

END.

Пример 13. Управление движением объекта.

Направление движения определяется нажатой клавишей (стрелки влево, вправо, вверх, вниз). Шаг перемещения вводится. Реализация движения характеризуется тем, что на каждом шаге запоминается образ области экрана, куда помещается курсор, затем при смещении курсора изображение восстанавливается.

PROGRAM Primer_13;

{ Программа управления движением курсора.

Курсор - прямоугольный объект, двигающийся вверх, вниз,

вправо, влево при нажатии соответствующих стрелок.

Выход при нажатии клавиши ESC }

uses Crt,Graph;

{ Модуль Crt необходим для использования Readkey }

PROCEDURE BadKey;

{ Процедура формирует звук при нажатии неправильной клавиши }

BEGIN

Sound (500); Delay (100); Sound (400);

Delay (200); Nosound

END;

var p,pc: Pointer;

{pc - указатель на образ курсора,

p - указатель на образ изображения "под" курсором }

grm,grd,curx,cury,curx0,cury0,lx,ly,hx,hy:integer;

size,c:word; ch:char;

{ grd,grm - переменные для номеров графических драйверов и режима

curx,cury - координаты текущего положения курсора

curx0,cury0 - переменные для запоминания координат курсора

lx,ly - ширина и длина курсора прямоугольного вида

hx,hy - шаги движения курсора по горизонтали и вертикали }

BEGIN

WriteLn ('Введите размеры курсора и шаги движения');

ReadLn (lx,ly,hx,hy);

{ Установка значения системной переменной для обеспечения

совместимости работы модулей Crt и Graph }

DirectVideo:=FALSE;

grd:=0; InitGraph (grd,grm,'D:\Tp\Bgi');

{ Инициализация графического режима с автоматическим

определением подходящего драйвера }

c:=GetColor; { c - цвет изображения }

size:=ImageSize (0,0,lx,ly);

{ size - количество байтов для изображения курсора }

GetMem (pc,size); GetMem (p,size);

{ Выделяются области для хранения образа курсора,

и образа изображения под курсором }

SetFillStyle (1,c); { устанавливается тип и цвет закраски курсора }

GetImage (0,0,lx,ly,p^);

{ p указывает на область памяти, где хранится изображение,

которое будет "закрыто" курсором }

curx:=0; cury:=0;

Bar (0,0,lx,ly); GetImage (0,0,lx,ly,pc^);

{ pc указывает на область памяти с изображением курсора }

SetColor (6); SetFillStyle (1,2);

Bar3d (150,150,200,30,10,TRUE);

{ Параллелограмм, на фоне которой происходит движение }

Repeat { Цикл по вводу символа }

ch:=ReadKey; { Ввод очередного символа }

If Ord(ch)=0

then { Нажата управляющая клавиша }

begin

ch:=ReadKey;

curx0:=curx; cury0:=cury;

{ В переменных curx,cury запоминаются координаты курсора }

Case Ord(ch) of

77: If curx
then curx:=curx+hx; { Шаг вправо }

75: If curx>hx

then curx:=curx-hx; { Шаг влево }

72: If cury>hy

then cury:=cury-hy; { Шаг вверх }

80: If cury
then cury:=cury+hy { Шаг вниз }

else BadKey { Нажата "неправильная" клавиша }

end;

If (curx<>curx0) OR (cury<>cury0)

then begin

PutImage (curx0,cury0,p^,0);

{ Восстановить изображение, которое было "закры-

то" курсором }

GetImage (curx,cury,curx+lx, cury+ly,p^);

{ Запомнить то изображение, которое будет "зак-

рыто" курсором }

PutImage (curx,cury,pc^,0);

{ Установить курсор в новое положение }

end

end

else BadKey

until Ord(ch)=27;

CloseGraph

END.

Пример 14. Вычеркивание по выбору граф элементы.

uses graph,crt;

var gd,gm,choice:integer;

begin

initgraph(gd,gm,'');

outtext('Выберите длину отрезка:1-50 точек(1), 2-150 точек(2)');

readln(choice);

case choice of

1:LINE (295, 240,345, 240);

2:LINE (245, 240,395, 240);

end;

repeat;

until keypressed;

closegraph;

end.

Пример 15. Выполнение граф построений

uses graph,crt;

var gd,gm:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

LINE (150, 100,67, 100);

LINE (67, 100,102, 68);

LINE (102, 68,150, 100);

floodfill (100, 90, 15);

delay(2000);

clearviewport;

bar(73, 49,141, 109);

delay(2000);

clearviewport;

LINE (73, 49,103, 79);

LINE (103, 79,92, 120);

LINE (92, 120,50, 120);

LINE (50, 120,31, 79);

LINE (31, 79,73, 49);

floodfill (90, 90, 15);

delay(2000);

clearviewport;

LINE (73, 49,111, 49);

LINE (111, 49,132, 71);

LINE (132, 71,111, 93);

LINE (111, 93,73, 93);

LINE (73, 93,52, 71);

LINE (52, 71,73, 49);

floodfill (100, 90, 15);

repeat;

until keypressed;

closegraph;

end.

Пример 16. Начертить N окружностей.

uses graph,crt;

var gd,gm,n,i:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

outtext('Введите кол-во окружностей');

readln(n);

clearviewport;

FOR i:= 1 TO n do

begin;

CIRCLE (Random(640),Random(480), 50)

end;

repeat;

until keypressed;

closegraph;

end.

Пример 17. Построить многоугольник со сторонами 60 и 20 точек.

uses graph,crt;

var gd,gm,x,x1,y,y1:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

outtextxy(20,0,'Введите координаты левого верхнего угла прямоугольника (x,y)');

readln(x);

readln(y);

outtextxy(20,10,'Введите координаты правого нижнего угла прямоугольника (x1,y1)');

readln(x1);

readln(y1);

rectangle(x,y,x1,y1);

repeat;

until keypressed;

closegraph;

end.

Пример 18. Построить и закрасить круг.

uses graph,crt;

var gd,gm,x,y,r:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

outtextxy(40,0,'Введите координаты центра окружности');

readln(x);

readln(y);

outtextxy(40,20,'Введите радиус окружности');

readln(r);

CIRCLE (x, y, r);

floodfill(x,y, 15);

repeat;

until keypressed;

closegraph;

end.

Пример 19. Построить из окружностей рисунок облака.

uses graph,crt;

var gd,gm:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

SetFillStyle(1, 15);

setcolor(15);

CIRCLE (320, 240, 100);

floodfill (320, 240, 15);

CIRCLE (220, 240, 80);

floodfill (200, 240, 15);

CIRCLE (420, 240, 80);

floodfill (440, 240, 15);

repeat;

until keypressed;

closegraph;

end.

Пример 20. Построение звезды.

uses graph,crt;

var gd,gm:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

setcolor(15);

line(220,240,320,100);

line(320,100,420,240);

line(220,140,420,140);

line(220,140,420,240);

line(420,140,220,240);

delay(3000);

end.

Пример 21. Построение квадрата.

uses graph,crt;

var gd,gm,x,y,side:integer;

begin

initgraph(gd,gm,'c:\bp\bgi');

outtextxy(30,0,'Введите сторону квадрата.');

readln(side);

clearviewport;

outtextxy(30,0,'Введите координаты центра квадрата(X и Y через ENTER)');

readln(x);

readln(y);

clearviewport;

rectangle(x-side,y - side ,x + side , y + side );

repeat;

until keypressed;

closegraph;

end.

Пример 22. Рисование луны.

uses crt,graph;

var gd,gm,choice:integer;

label 1,2,3;

begin;

clrscr;

writeln('1.полнолуние, 2.1/2 луны, 3.месяц');

readln(choice);

initgraph(gd,gm,'c:\bp\bgi');

IF choice = 1 THEN GOTO 1;

IF choice = 2 THEN GOTO 2;

IF choice = 3 THEN GOTO 3;

halt;

1:

CIRCLE (320, 240, 100);

floodfill(320,240,15);

repeat;

until keypressed;

halt;

2 :

arc(320, 240, 90, 270, 100);

LINE (320, 140,320, 340);

floodfill(300,240,15);

repeat;

until keypressed;

halt;

3 :

arc(320, 240, 90, 270, 100);

arc(490, 240, 150, 210, 200);

floodfill(285,240,15);

repeat;

until keypressed;

halt;

closegraph;

end.

Пример 23. Построение треугольника по заданным координатам.

uses crt,graph;

var gd,gm,x,y,a,c:integer;

begin

clrscr;

writeln('Введите координаты центра звезды X и Y ');

readln(x);

readln(y);

writeln('Введите длину луча звезды (не меньше 90)');

readln(a);

initgraph(gd,gm,'c:\bp\bgi');

c:=round(3/4*a);

line(x,y-a,x+c,y+2*c);

line(x,y-a,x-c,y+2*c);

line(x+c,y+2*c,x-a-10,y-25);

line(x-c,y+2*c,x+a+10,y-25);

line(x+a+10,y-25,x-a-10,y-25);

delay(3000);

closegraph;

end.

Пример 24. Построение кораблика

uses graph,crt;

var gd,gm:integer;

a,h:real;

begin

initgraph(gd,gm,'c:\bp\bgi');

outtextxy (30,0,'Введите высоту и длину палубы (H и A через Enter)');

readln(h);

readln(a);

LINE (320 + round(a / 2), 240 - round(h / 2),320 + round(a/2), 240 + round(h/ 2));

LINE (320 + round(a / 2), 240 - round(h / 2),320 - round(a / 2), 240 - round(h / 2));

LINE (320 - round(a / 4), 240 + round(h / 2),320 + round(a / 2), 240 + round(h / 2));

LINE (320 - round(a / 4), 240 + round(h / 2),320 - round(a / 2), 240 - round(h / 2));

LINE (320, 240 - round(h / 2),320, 240 - round(h * 2));

LINE (320, 240 - round(h * 2),320 + round(a / 5), round(240 - h));

LINE (320, 240 - round(h),320 + round(a / 5),round( 240 - h));

repeat;

until keypressed;

closegraph;

end.

Пример25. Программа рисует звездное небо с 400 звездами, вспыхивающими постепенно, полную желтую луну.

Program Work_8;

Uses Graph, Crt;

Var k, gd, gm: integer;

Begin

Gd:=detect;

InitGrapf(gd, gm, ‘’);

Randomize;

For i:=1 to 400 do

Begin

Putpixel(random(640), random(480), random(15)+1);

Deley(10); {задержка – пауза в 1 сек}

End;

SetColor(14); {задаем цвет окружности 14 - желтый}

Circle(300,100,30);

Floodfill(310,110,yellow); {закрашиваем луну}

Repeat until keypressed; {пока не нажата любая клавиша}

Closegraph; {закрываем графический режим}

End.

Полярная система координат

В полярной системе координат положение точки определяется полярным радиусом R и углом theta, образуемым полярным радиусом с полярной осью. Если в декартовой системе координат предельно простое выражение y=kx определяет прямую линию, то это же выражение, переписанное в форме R=k*theta, уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. В цилиндрической системе к полярному радиусу и углу добавляется еще одна координата - z, которую можно интерпретировать как высоту точки над плоскостью, в которой вращается полярный радиус. Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы:

X=R* Cos (theta)

Y=R* Sin(theta)

Соответственно, для перехода от декартовой системы к полярной применяют формулу:

R=Sqr(X*X+Y*Y)

и угол вычисляется как Atn(Y/X) (если X не равен 0)

Фигуры в полярных координатах

Формулы кривых, записанных в полярной системе координат, вычисляются гораздо проще, чем в декартовой. Например, уравнение окружности с радиусом 0.9 вокруг точки отчета выглядит очень просто

R=0.9, что подразумевает следующие вычисления:

R*Cos(theta)

R*Sin(theta)

где угол theta изменяется от 0 до 2π радиан и определяет декартовы координаты X и Y окружности в полярной системе

Для объяснения вышесказанного приведем небольшой листинг программы, рисующей окружность:

Dim x As Single, y As Single

Dim twoPi As Single, I As Single, R As Single

twoPi = Atn(1) * 8

Scale (-2, 2)-(2, -2)

For I = 0 To twoPi Step 0.05

R = 0.9

x = R * Cos(I)

y = R * Sin(I)

PSet (x, y)

Next I

Полярные координаты позволяют рисовать намного более сложные и красивые фигуры. Например, можно нарисовать четырехлистный клевер. Его формула выглядит как R = Cos (2*theta), где угол theta меняется от 0 до 2π радиан (от 0 до 360 градусов)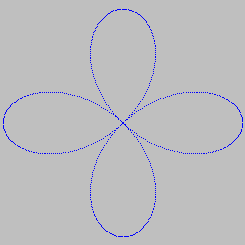

Листинг для клевера


Dim x As Single, y As Single

Dim twoPi As Single, I As Single, R As Single

twoPi = Atn(1) * 8

Scale (-2, 2)-(2, -2)

For I = 0 To twoPi Step 0.01

R = Cos(2 * I)

x = R * Cos(I)

y = R * Sin(I)

PSet (x, y)

Next I

Для трехлистного цветка используйте формулу R = Cos (3*theta)

На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен.

• 
  Дельтоида
  
• 
  Астроида
  
• 
  Кардиоида
  
• 
  Лимакона (Улитка Паскаля)
  
• 
  Спираль Архимеда
  
• 
  Логарифмическая спираль
  
• 
  Кохлеоида
  
• 
  Строфоида
  
• 
  Freeth's Nephroid
  
• 
  Овалы Кассини
  
• 
  Лемниската Бернулли
  

Окружность

Итак, формула R=a определяет обычную окружность, а коэффициент a влияет на ее радиус

"Пируэты" окружности

Возьмем теперь одну окружность и поместим ее внутрь другой. Все кривые, которые будет вычерчивать точка на окружности, катящейся внутри другой окружности, будут относиться к семейству гипоциклоид (от греч. гипо - под, внизу и киклоидес - кругообразный). Как вы думаете, какую траекторию опишет точка окружности, которая катится внутри другой окружности? Как это ни странно звучит, но она может быть даже прямой! Для этого радиус внутренней окружности должен быть в два раза меньше радиуса внешней. Первым это заметил и описал Николай Коперник. Если же радиус внутренней окружности меньше радиуса большой окружности в три раза, то точка опишет кривую Штейнера (дельтоиду).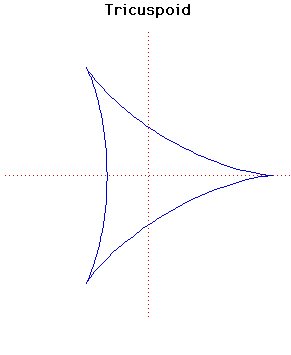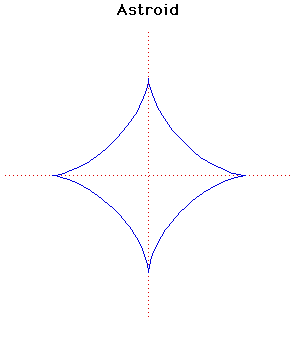


Уменьшив радиус теперь в четыре раза, мы получим астроиду

Астроида (Astroid)

Астроида (греч. астрон - звезда) - кривая, которая внешне напоминает стилизованное изображение звезды.

Формула x = a* cos(t)^3, y = a* sin(t)^3 рисует астроиду,
где коэффициент a влияет на вытянутость фигуры.

Эпициклоиды

Рассмотрим другой случай. Будем вращать окружность не внутри другой (опорной) окружности, а по ее внешней стороне. Теперь, все получаемые кривые будут относиться к семейству эпициклоиды (греч.эпи - на, над). К таким фигурам относятся кардиодида и улитка Паскаля