Методичка 2 (1). Методическое пособие для выполнения расчётнографической работы Расчёт статически определимой консольной балки на прочность и жёсткость

• Название: Методическое пособие для выполнения расчётнографической работы Расчёт статически определимой консольной балки на прочность и жёсткость
• Дата: 10.03.2022
• Размер: 0.51 Mb.
• Имя файла: Методичка 2 (1).doc
• Тип: Методическое пособие; #390055
• страница: 3 из 3

3. Подбор поперечных сечений балки. Оптимальная форма сечения.

. Из условия прочности при изгибе и одинаковом допускаемом напряжении на растяжение и сжатие [σ] = 160 МПа необходимо подобрать поперечные сечения балок требуемых форм, сравнить их по массе и выбрать оптимальную форму сечения балки. Наибольшее значение изгибающего момента рассматриваемой балки (рис.3) равно M_max= 25,66 кН·м. Условие прочности по нормальным напряжениям имеет вид: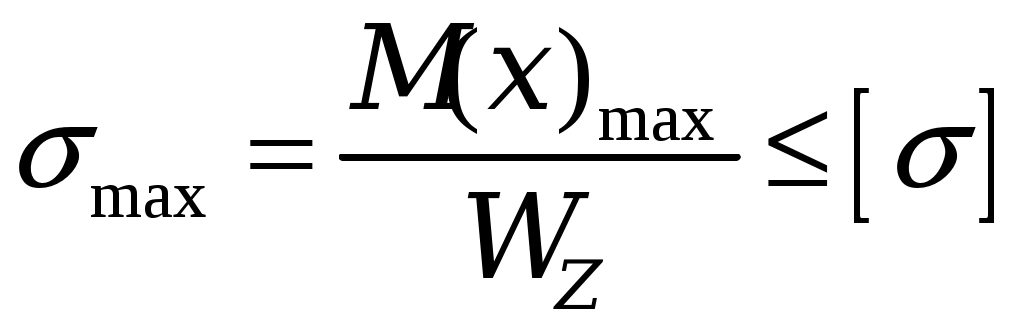

,

отсюда следует выражение для требуемого момента сопротивления W_z: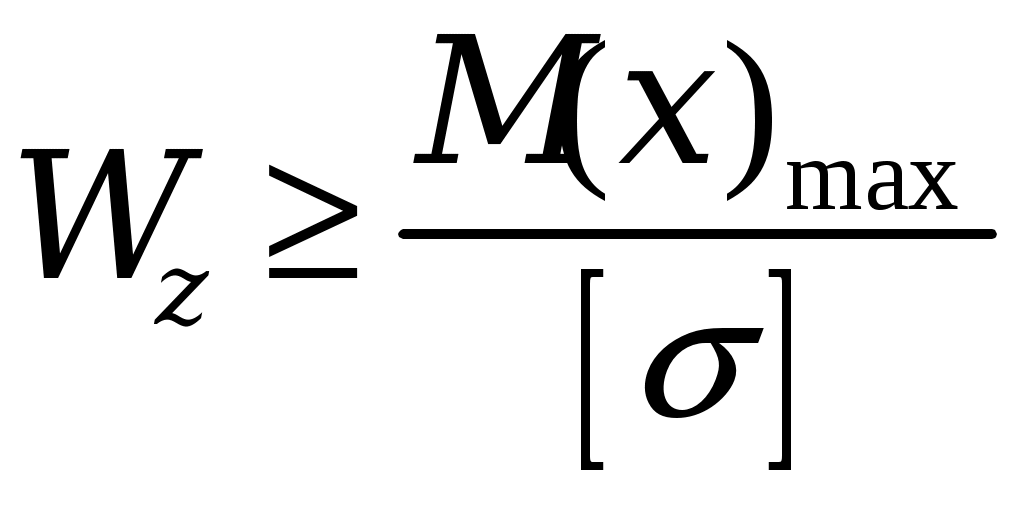

, (7)

из которого определяются геометрические параметры требуемого сечения..

a) Круглое сечение. Осевой момент сопротивления для круглого поперечного сечения диаметра Dимеет вид: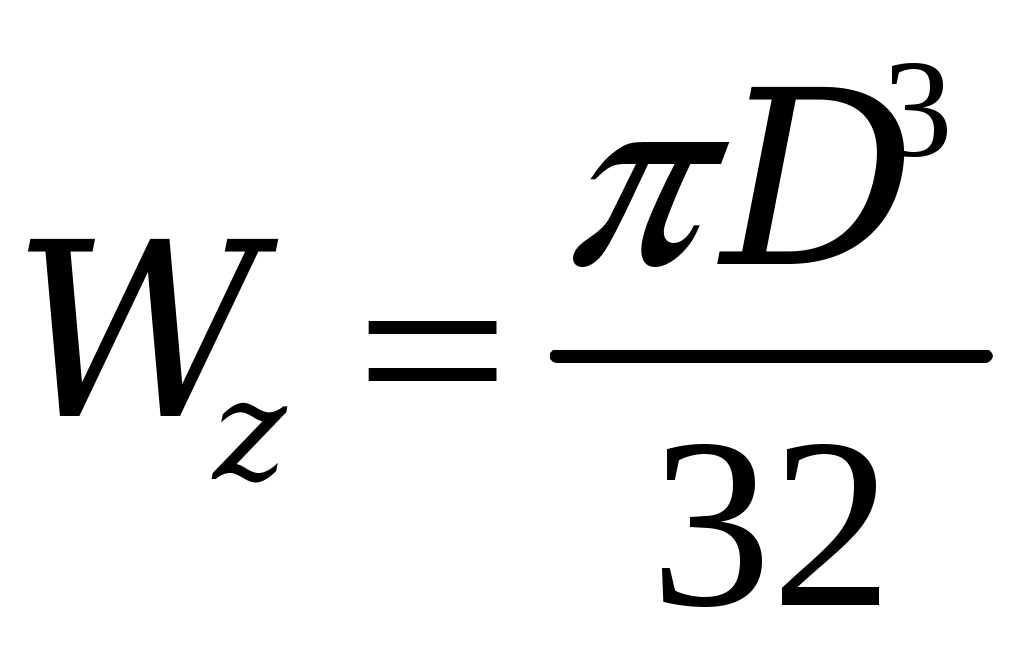

,

подставляя в формулу (7), получим:

.

Площадь поперечного сечения составит:

.

b) Квадратное сечение. Осевой момент сопротивления для квадратного поперечного сечения со стороной h имеет вид:

,

подставляя в формулу (7), получим:

.

Площадь поперечного сечения составит:

.

с) Прямоугольное сечение со сторонами h·3h. Максимальный осевой момент сопротивления для прямоугольного поперечного сечения со сторонами h·3h имеет вид:

,

подставляя в формулу (7), получим:

.

Площадь поперечного сечения составит:

.

d) Сечение из двух швеллеров. Определяем требуемый момент сопротивления для двух швеллеров, стыкуемых стенками, по формуле (7):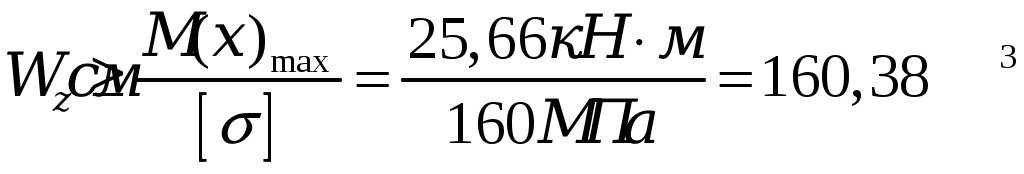

.

Для одного швеллера момент сопротивления составит 80,19 см³. По сортаменту прокатных профилей выбираем ближайший (с не меньшим моментом сопротивления) швеллер. Таковым будет швеллер №16 с моментом сопротивления W_z= 93,4см³ и площадью – A_ш=18,1 см².

Площадь поперечного сечения двух швеллеров A_d составит:

A_d= 2·18,1 см²= 36,2 см².

e) Сечение из двутавра. Имея величину требуемого момента сопротивления (160,38см³), подбираем по сортаменту подходящий двутавр. Им оказался двутавр №20 со следующими характеристиками: моментом сопротивления W_z= 184см³ и площадью поперечного сечения

A_е= 26,8 см².

Сравнение всех полученных поперечных сечений по массе, для изделий постоянного поперечного сечения и выполненных из одного материала, может быть заменено сравнением их площадей. Наиболее эффективной формой поперечного сечения, очевидно, будет форма с наименьшей площадью, каковой и является площадь поперечного сечения прокатного двутавра, проектируемого ещё в 19в. специально как балочного профиля.

Все полученные поперечные сечения для визуального сравнения их эффективности с точки зрения изгиба изображены в масштабе на рис. 7.



Рис. 7

4. Полная проверка прочности двутавровой балки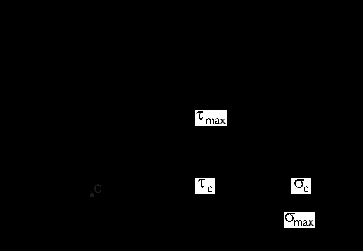



Рис. 8

Для подобранного сечения (двутавр№ 20) выпишем из сортамента необходимые геометрические характеристики, ориентируясь на буквенные обозначения идеализированного двутавра (рис. 8): h = 20 см; b = 10 см; d = 0,52 см;t= 0,84 см; I_z = 1840 см⁴; W_z = 184 cм³; S_z = 104 см³.

4.1. Проверка прочности по нормальным напряжениям. Производится для сечения с наибольшим значением изгибающего момента. В рассматриваемой балке это сечение с координатой 1.2 м, где изгибающий момент равен 25,66 кН·м.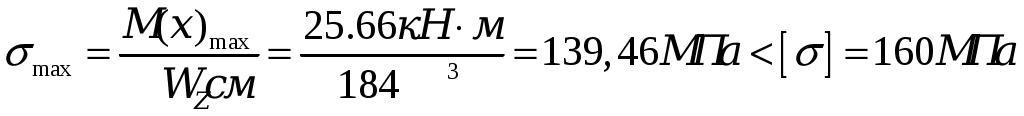

.

Недонапряжение (запас прочности по нормальным напряжениям) составляет:



4.2. Проверка прочности по касательным напряжениям. Производится для сечения с наибольшим значением поперечной силы. В балке это поперечная сила в сечении на опоре А, равная 20,82 кН. Наибольшие касательные напряжения возникают в середине стенки двутавра и определяются по формуле Журавского. Условие прочности записывается таким образом: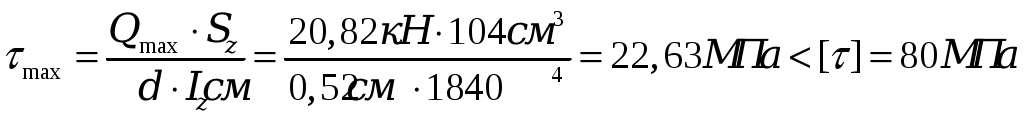

,

что говорит о почти четырёхкратном запасе прочности по касательным напряжениям.

4.3. Проверка прочности по третьей и четвёртой гипотезам. Для этих проверок выбираются сечения балки с достаточно большими поперечной силой и изгибающего момента и точка в поперечном сечении с достаточно большими касательным и нормальным напряжениями. Точка в поперечном сечении балки выбирается тоже с достаточно большими нормальными и касательными напряжениями. Для двутавра – это точка «с», точка соединения стенки и полки с напряжениями σ_с и τ_с (рис.8).

4.3.1. По третьей гипотезе прочности проверим сечение балки с характеристиками М =25,66 кН·м и Q=13,62кН (х=1.2м). Определим напряжения σ_с и τ_с: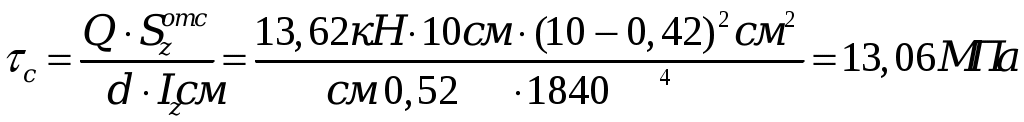

;

.

В соответствии с 3-й гипотезой прочности (наибольших касательных напряжений) получим:



4.3.2. По четвёртой гипотезе прочности проверим сечение балки с характеристиками М =5 кН·м и Q =20,82 кН (х = 0). Определим напряжения σ_с и τ_с: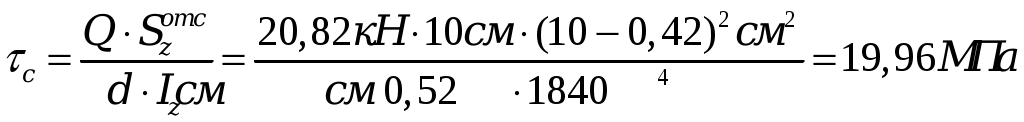



.

В соответствии с 4-й гипотезой прочности (наибольшей энергии формоизменения) получим:



Таким образом, произведена полная проверка прочности балки, показавшая её пригодность к эксплуатации при заданной нагрузке.
5. Расчёт балки на жёсткость

5.1. Для построения упругой линии балки, вычислим прогибы балки для начала, конца и середины каждого из грузовых участков. Воспользуемся для этого методом начальных параметров, именно, универсальным уравнением упругой линии балки: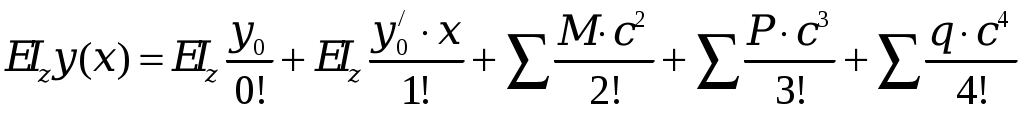

. (8)

Для осуществления процесса формирования слагаемых уравнения (8) в части учёта первоначально заданных равномерно распределённых нагрузок, последние представлены на рисунке 9 так, как это требуется в методе начальных параметров. Именно, исходная нагрузка продолжается до конца балки, а в месте её фактического окончания прикладывается непрерывная нагрузка, равная исходной по величине и обратная по направлению (на рис.8 показана пунктиром).

Необходимо записать уравнение (8) в физических величинах и определить начальные параметры у₀ и у^/₀ . Очевидно, что прогиб балки в начале координат, на опоре А равен нулю, то есть первый начальный параметр у₀ = 0. Угол поворота сечения балки в начале координат у^/₀ определяется из условия равенства нулю прогиба балки на другой опоре - В.



Рис. 9

Для определения начального параметра у^/₀ потребуем равенства нулю уравнения (8) при x = 5м: 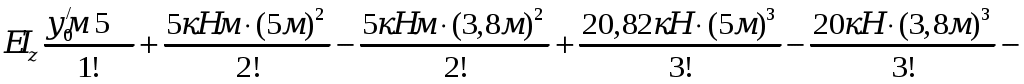, или



,

откуда следует: .

На рисунке 10 буквами a, b, c, dиeобозначены точки, определяющие грузовые участки и их середины. Например, точка a отвечает середине первого участка, точка b – сечению первого и второго участков и так далее. Этими же буквами будем обозначать вычисления соответствующих прогибов.

a).

;

b).

;

с).



d).

;

е).







По вычисленным прогибам на рис. 10 в масштабе вычерчена упругая линия балки.



Рис. 10
5.2. После построения упругой линии балки можно примерно с той же точностью определить максимальные прогибы в пролёте балки и на её консоли графоаналитическим способом. Проведём параллельно оси х-х касательные к линии прогибов в пролёте и на консоли и, измерив расстояния от оси до точек касания, определим их численные значения. Оказалось:

для пролёта ;

для консоли .

Проверим жёсткость балки в пролёте балки и на её консоли, по величинам относительных прогибов f_max/l:

для пролёта ,

для консоли .

Видно, что на консоли требования жёсткости не выполняются, поэтому сечение балки должно быть пересмотрено в сторону увеличения и подобрано из условий удовлетворения требуемой жёсткости но консоли.

4. Задание для выполнения РГР

4.1. Для заданной статически определимой, однопролётной консольной стальной балки требуется:

4.1.1 Определить опорные реакции;

4.1.2. Построить эпюры поперечных сил и изгибающих моментов;

4.1.3. Из условия прочности при изгибе и одинаковом допускаемом напряжении на растяжение и сжатие, подобрать следующие поперечные сечения балки: круг, квадрат, прямоугольник с размерами h · 3h, два швеллера, двутавр; сравнить найденные сечения по массе и выбрать оптимальную форму сечения балки;

4.1.4. Произвести полную проверку прочности двутавровой балки:

- по нормальным напряжениям;

- по касательным напряжениям;

- по 3-й и 4-й гипотезам прочности.

4.1.5. Построить упругую линию балки, вычислив прогибы балки для начала, конца и середины каждого грузового участка и проверить жёсткость балки в пролёте балки и на её консоли, по величинам относительных прогибов f_max/l.

Указание к п.4.1.6. Максимальные прогибы f _max в пролёте и на консоли определить измерениям по графическому изображению линии прогибов.

4.2. Допускаемое напряжение на растяжение и сжатие составляет значение [σ] = 160 МПа;

- допускаемое касательное напряжение составляет значение [τ] = 80 МПа;

- модуль упругости стали равен Е=2, 06·10⁵ МПа;

- допускаемая величина относительного прогиба равна [f_max/l]=1/400.

4.3. Геометрическая схема балки для всех заданий одинакова.

Все нагрузки, представленные на схеме балки, имеют положительное направление.

Индивидуальности состава задания отвечают величины и направления действующих нагрузок и линейные размеры балки, определяемые с помощью индивидуального шифра.

Каждому студенту присваивается свой пятизначный шифр. Каждая цифра шифра размещается по порядку под соответствующим столбцом задания. Шифр записывается подряд четыре раза и охватывает все двадцать столбцов задания. Каждому номеру шифра столбца отвечает такой же номер строки, на их пересечении размещается элемент исходной информации задания. Например, шифр составляет значение 45076, тогда под всеми двадцатью столбцами задания будем иметь такую череду цифр 4-5-0-7-6-4-5-0-7-6-4-5-0-7-6-4-5-0-7-6.

Первая цифра 4 принадлежит первому столбцу задания, относящемуся к сосредоточенной силе F₁, величина этой силы отвечает строке с той же цифрой 4. Таким образом, F₁ = 20 кН. Иначе говоря, искомая величина находится на пересечении столбца и строки, определяемыми цифрой 4.

Вторая цифра шифра 5 принадлежит второму столбцу задания и относится к знаку силы F₁. Знак силы – «минус» определяется вторым столбцом и строкой с цифрой 5 и так далее.

4.4. Расчётно-графическая работа выполняется на листах белой бумаги формата А4 с полями (2,0см – левое, 1,5см – правое, 1,5см верхнее и нижнее), пронумеровывается, начиная со второго листа (первый лист – титульный не нумеруется), и сшивается в брошюру. Текст и формулы пишутся рукой, титульный лист может быть выполнен на компьютере (см. п.3).Схемы и эпюры чертятся карандашом, в изображениях эпюр соблюдается масштаб. Необходимый комментарий представляется в соответствии с приведённым «Примером выполнения РГР». В результатах вычислений (с округлениями по Гауссу) приводятся две значащих цифры после запятой, например: вычислено значение 4,456027, приводится в тексте 4,45; вычислено 0,0345500 приводится 0,035 и так далее.
Литература

1. Александров А.В. , Потапов В.Д., Державин Б.П. Сопротивление материалов, - М.: Высшая школа, 1995. 560 с.

2. Беляев Н.М. Сопротивление материалов, – М.: Наука, 1965.856с.

3. Логвинов В.Б., Петров И.А. Сопротивление материалов, Простые виды нагружения и элементарные задачи. – Новочеркасск: изд-во ЮРГТУ, 2004. 244 с.

4. Миролюбов И.Н. и др. Пособие к решению задач по сопротивлению материалов, – М.: Высшая школа. 1985. 399с.

5. Очинский В.В., Кожухов А.А., Лобейко Ю.А. Сопротивление материалов, краткий именной и терминологический словарь, - Ставрополь: Агрус, 2005. 104 с.

6. Писаренко Г.С. и др. Сопротивление материалов, – Киев: Вища школа. 1986. 776 с.

7. Стёпин П.А. Сопротивление материалов.- М.: Высшая школа, 1988. 366 с.

Содержание

1. Краткая характеристика работы …………………….

2. Сведения из теории …………………………………

3. Пример выполнения РГР ………………………….

4. Задание для выполнения РГР ………………………………….

5. Приложение – сортамент прокатных профилей…………..
Компьютерная графика К.В. Путырский