Математический анализ для экономистов. Методическое пособие для заочной формы обучения. Выбор темы контрольной работы выбирается по первой букве фамилии студента и последней цифре номера зачетной книжки
 Скачать 2.83 Mb. Скачать 2.83 Mb.
|
  МАТЕМАТИЧЕСКИЙ АНАЛИЗ. (Ч. 2) МАТЕМАТИЧЕСКИЙ АНАЛИЗ. (Ч. 2)Учебно – методическое пособие для заочной формы обучения. Выбор темы контрольной работы: выбирается по первой букве фамилии студента и последней цифре номера зачетной книжки.
ТЕМАТИЧЕСКИЙ ПЛАН. Тема 1. Неопределённый интеграл. Тема 2. Определённый интеграл. Тема 3. Дифференциальные уравнения. СОДЕРЖАНИЕ КУРСА. Тема 1. Первообразная функции и неопределённый интеграл. Основные свойства неопределённого интеграла. Интегралы основных элементарных функций. Интегрирование путём замены переменной. Метод интегрирования по частям. Интегрирование простейших рациональных дробей. Интегрирование тригонометрических функций. Тема 2. Определённый интеграл и его свойства. Теорема о существовании определённого интеграла. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Методы замены переменной и интегрирование по частям в определённом интеграле. Геометрические приложения определённого интеграла. Несобственные интегралы. Приближённое вычисление определённых интегралов. Тема 3. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными. Линейные дифференциальные уравнения. Уравнения Бернулли. Линейные дифференциальные уравнения с постоянными коэффициентами. ПЕРЕЧЕНЬ ЗАДАНИЙ. Неопределенный интеграл функции одной переменной Вычислить неопределенный интеграл методом непосредственного интегрирования ( 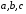 – произвольные константы, не равные нулю). Сделать проверку (посредством дифференцирования). – произвольные константы, не равные нулю). Сделать проверку (посредством дифференцирования).
Определенный интеграл функции одной переменной Вычислить определенные интегралы.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

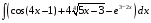
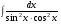
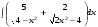 1
1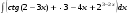
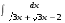
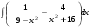 2
2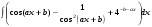
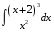
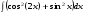 3
3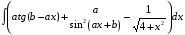
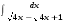
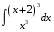 4
4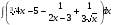
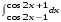
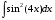 5
5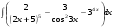
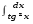
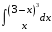 6
6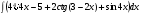
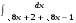
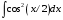 7
7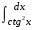
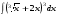
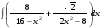 8
8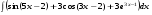
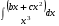
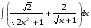 9
9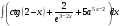
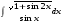
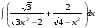 10
10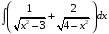
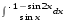
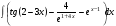 11
11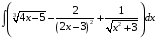
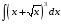
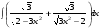 12
12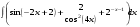
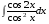
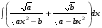 13
13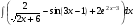
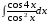
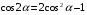
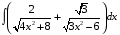 14
14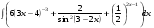
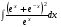
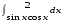 15
15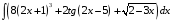
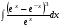
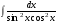 16
16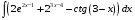
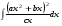
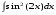 17
17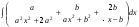
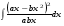
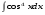
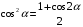 18
18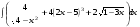
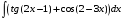
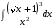 19
19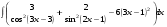
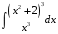
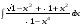 20
20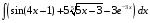
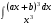
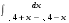 21
21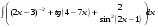
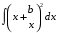
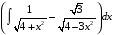 22
22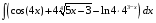
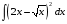
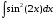
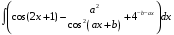
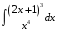
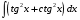 25
25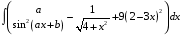
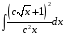 26
26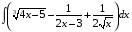
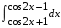
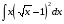 27
27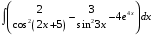
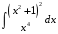
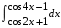 28
28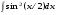 29
29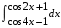
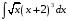
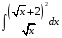
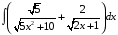 31
31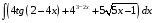
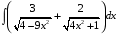
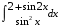 32
32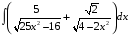
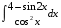
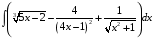
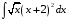
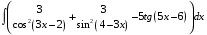 34
34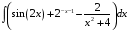
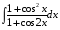
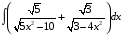 35
35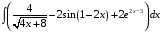
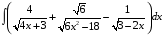
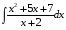 36
36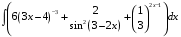
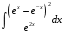
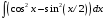 37
37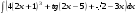
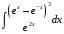
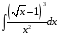 38
38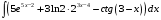
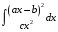
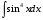
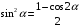 39
39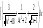
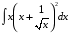
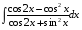 40
40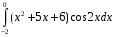
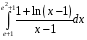
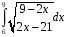
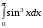
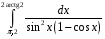 1
1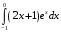
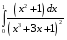
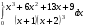
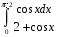
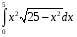 2
2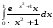
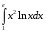
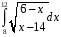
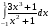
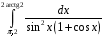 3
3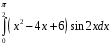
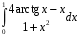
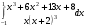
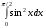
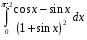 4
4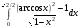
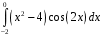
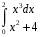
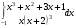
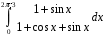 5
5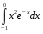
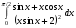
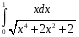
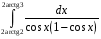
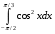 6
6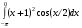
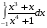
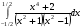
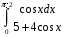
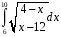 7
7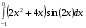
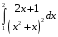
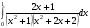
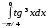
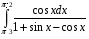 8
8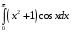
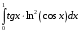
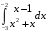
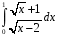
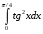 9
9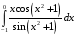
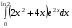
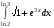
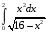
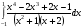 10
10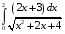
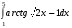
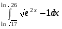
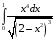
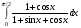 11
11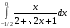
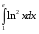
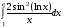
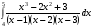
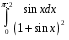 12
12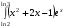
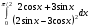
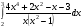
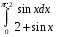
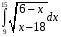 13
13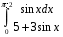
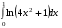
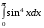
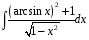
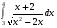 14
14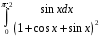
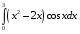
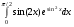
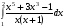
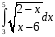 15
15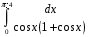
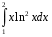
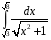
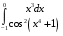
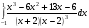 16
16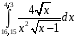
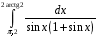
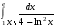
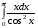
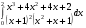 17
17
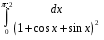 18
18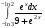
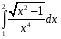
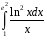
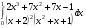
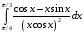 19
19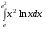
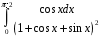
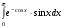
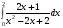
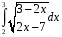 20
20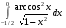
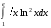
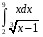
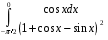
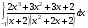 21
21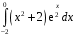
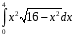
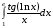
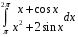
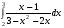 22
22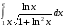
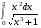
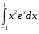
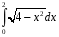
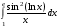
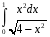
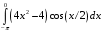
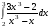
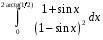 24
24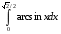
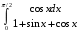
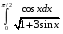
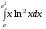
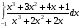 25
25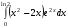
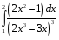
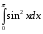
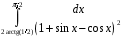 26
26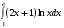
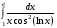
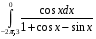
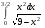 27
27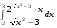
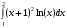
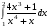
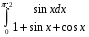 28
28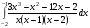
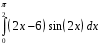
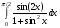
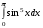
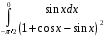 29
29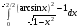
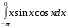
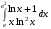
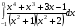
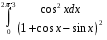 30
30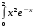
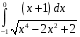
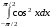 31
31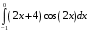
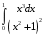
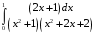
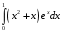
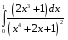
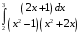
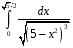 34
34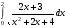
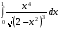
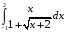
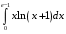
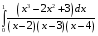
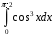 36
36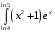
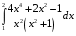
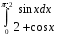
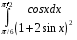
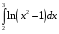
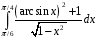
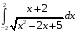 38
38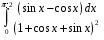
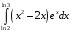
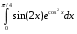
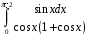
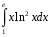
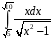
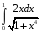
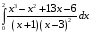 40
40