Математический анализ для экономистов. Методическое пособие для заочной формы обучения. Выбор темы контрольной работы выбирается по первой букве фамилии студента и последней цифре номера зачетной книжки
 Скачать 2.83 Mb. Скачать 2.83 Mb.
|
|
Определенный интеграл Теоремы общего характера Для вычисления определенного интеграла основной является теорема Ньютона – Лейбница: если 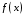 непрерывна на непрерывна на 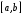 и и 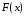 первообразная для первообразная для 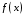 на на 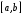 , то , то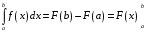 (4.23) (4.23)Пусть 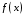 — функция, интегрируемая на — функция, интегрируемая на 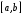 , , 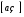 , , 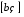 . Тогда, независимо от независимо от взаимного расположения точек . Тогда, независимо от независимо от взаимного расположения точек 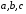 она интегрируема и в двух других промежутках, и имеет место равенство она интегрируема и в двух других промежутках, и имеет место равенство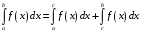 (4.24) (4.24)Имеют место формулы: 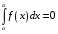 и и 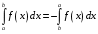 (4.25) (4.25)Пусть 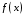 и и 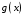 — функции, интегрируемые на — функции, интегрируемые на 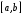 . Тогда, произведение . Тогда, произведение 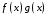 также интегрируемо на этом отрезке. также интегрируемо на этом отрезке.Если 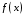 — функция, интегрируемая на — функция, интегрируемая на 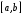 , и , и 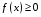 для для 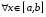 , то , то 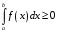 . .Если 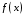 и и 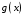 — функции, интегрируемые на — функции, интегрируемые на 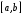 , и , и 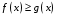 для для 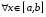 , то , то 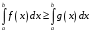 . .Теорема о среднем значении. Пусть 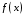 интегрируема и ограничена на интегрируема и ограничена на 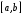 и и 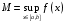 , , 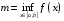 — соответственно, верхняя и нижняя грани — соответственно, верхняя и нижняя грани 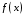 на на 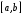 . Тогда, существует такое число . Тогда, существует такое число 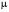 , что: , что: 1) 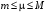 ; и, 2) ; и, 2) 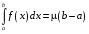 . .Формулы общего характера Пусть 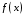 — функция, интегрируемая на — функция, интегрируемая на 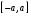 , и удовлетворяющая на этом отрезке соотношению , и удовлетворяющая на этом отрезке соотношению 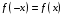 (такую функцию называют четной); тогда (такую функцию называют четной); тогда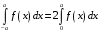 Пусть 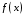 — функция, интегрируемая на — функция, интегрируемая на 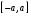 , и удовлетворяющая на этом отрезке соотношению , и удовлетворяющая на этом отрезке соотношению 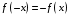 (такую функцию называют нечетной); тогда (такую функцию называют нечетной); тогда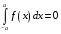 Замена переменного в определенном интеграле Формула 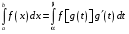 действительна при следующих условиях: Функция 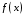 непрерывна на отрезке непрерывна на отрезке 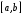 ; ;Отрезок 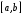 является множеством значений функции является множеством значений функции 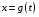 , определенной на отрезке , определенной на отрезке 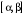 ; ;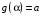 ; ; 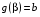 . .Формула интегрирования по частям Если каждая из функций 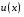 и и 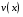 имеет на отрезке имеет на отрезке 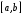 непрерывную производную, то справедлива следующая формула непрерывную производную, то справедлива следующая формула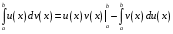 Геометрические приложения определенного интеграла Площадь криволинейной трапеции Площадь фигуры, называемой криволинейной трапецией, лежащей под графиком 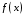 и неотрицательной на отрезке и неотрицательной на отрезке 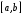 равна равна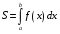 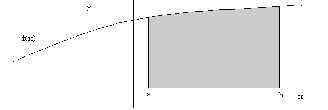 Площадь криволинейного сектора Площадь фигуры, называемой криволинейным сектором, ограниченной графиком 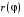 и двумя лучами, составляющими с полярной осью углы и двумя лучами, составляющими с полярной осью углы 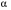 и и 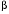 имеет площадь имеет площадь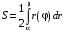 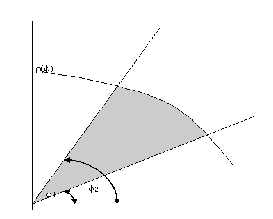 Вычисление объема вращения 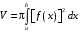 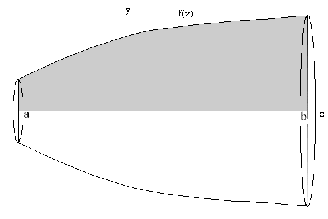 Длина дуги кривой. Если плоская кривая L задана параметрически 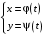 , , 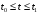 , ,причем 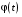 и и 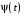 - непрерывно дифференцируемые функции, то она имеет длину, вычисляемую по следующей формуле - непрерывно дифференцируемые функции, то она имеет длину, вычисляемую по следующей формуле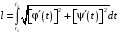 Если плоская кривая L – график непрерывно дифференцируемой функции 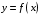 и и 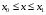 , то длина этой кривой вычисляется по формуле , то длина этой кривой вычисляется по формуле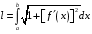 В полярных координатах 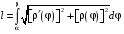 Примеры Задача 1.Вычислить интеграл: 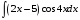 . .Решение: применяя интегрирование по частям, получаем 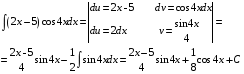 Задача №2: Вычислить интеграл: 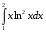 Решение: 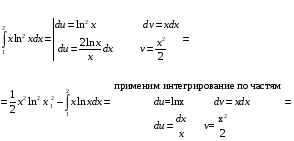 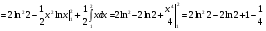 Задача №3: Вычислить интеграл: 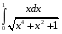 Решение: 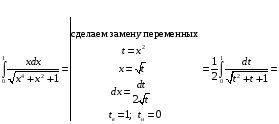 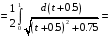 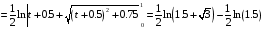 Задача №4: Вычислить интеграл: 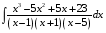 Решение: 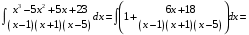 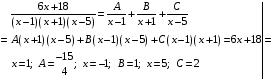 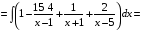 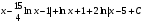 Задача №5: Вычислить интеграл: 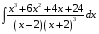 Решение: 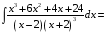 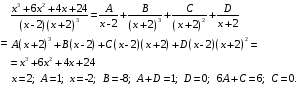  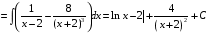 Задача №6: Вычислить интеграл: 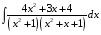 Решение: 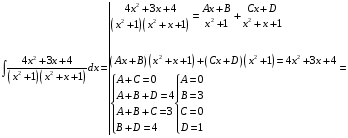 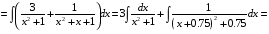 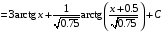 Задача №7: Вычислить интеграл: 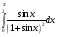 Решение: 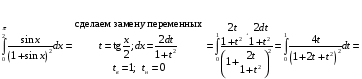 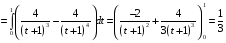 Задача №8: Вычислить интеграл: 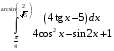 Решение: 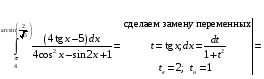 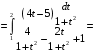 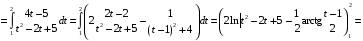 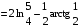 Задача №9: Вычислить интеграл: 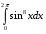 Решение: 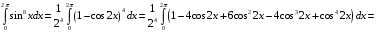 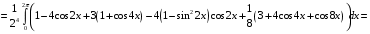 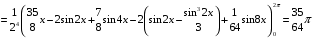 Задача №10: Вычислить интеграл: 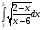 Решение: 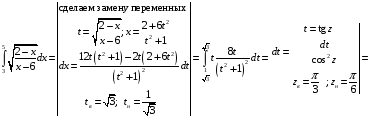 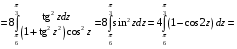 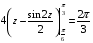 Задача №11: Вычислить интеграл: 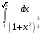 Решение: 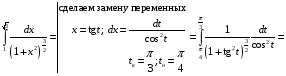 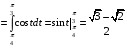 Задача №12: Вычислить интеграл: 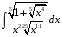 Решение: 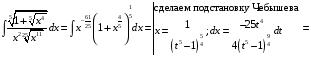 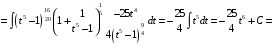 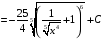 Функции многих переменных Частные производные. Геометрическая интерпретация частной производной. Пусть функция  определена в некоторой окрестности точки определена в некоторой окрестности точки 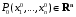 . Функция . Функция  называется дифференцируемой по называется дифференцируемой по 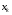 , если существует предел разностного отношения , если существует предел разностного отношения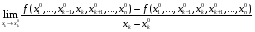 (5.1) (5.1)этот предел называется частной производной функции  (по (по 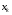 ) в точке ) в точке 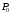 и обозначается и обозначается 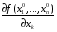 или или 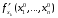 . .Таким образом, частная производная функции  равна обыкновенной производной функции действительного переменного равна обыкновенной производной функции действительного переменного 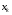 , которая получается из , которая получается из  , если переменные , если переменные 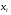 для для 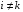 положить равными положить равными 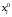 . .Для нахождения производной более высоких порядков, например порядка  , применяется специальная формула (5.2). Эта формула получается в результате индукции при рассмотрении частных производных более низкого порядка. , применяется специальная формула (5.2). Эта формула получается в результате индукции при рассмотрении частных производных более низкого порядка.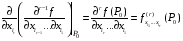 (5.2). (5.2).Рассмотрим геометрический смысл частной производной на примере функции 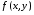 , которая дифференцируема по каждой из переменных в точке , которая дифференцируема по каждой из переменных в точке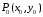 . По определению . По определению 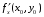 есть число, равное есть число, равное 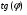 , где , где 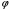 - угол между касательной к кривой пересечения плоскости П и графика функции - угол между касательной к кривой пересечения плоскости П и графика функции  и плоскостью и плоскостью 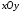 (см. рисунок ____ ). Аналогично и с (см. рисунок ____ ). Аналогично и с 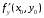 . .Полный дифференциал. Производная по направлению и градиент. Пусть область определения 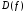 функции функции  содержит окрестность точки содержит окрестность точки 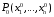 , , 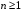 . Функция . Функция  называется дифференцируемой в точке называется дифференцируемой в точке 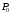 , если для любых , если для любых 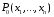 из этой окрестности из этой окрестности 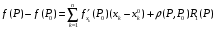 (5.3), (5.3), где 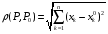 и и 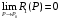 . .Линейная часть 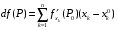 приращения приращения 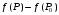 называется полным дифференциалом функции называется полным дифференциалом функции  в точке в точке 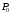 . .График функции 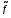 , определяемой равенством (5.4),называется касательной плоскостью к графику функции , определяемой равенством (5.4),называется касательной плоскостью к графику функции  в точке в точке 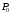 . . 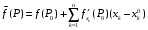 (5.4) (5.4)Если  дифференцируема в точке дифференцируема в точке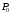 , то , то  непрерывна в непрерывна в 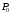 и дифференцируема по каждому из переменных и дифференцируема по каждому из переменных 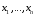 . Однако если функция непрерывна и дифференцируема по каждому из переменных . Однако если функция непрерывна и дифференцируема по каждому из переменных 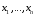 в точке в точке 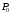 , то она не обязательно дифференцируема в этой точке. Если же , то она не обязательно дифференцируема в этой точке. Если же  непрерывно дифференцируема в точке непрерывно дифференцируема в точке 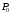 , то , то  дифференцируема в точке дифференцируема в точке 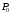 . . Если  дифференцируема в точке дифференцируема в точке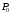 , то существует производная по направлению функции , то существует производная по направлению функции  в в 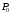 относительно произвольного единичного вектора относительно произвольного единичного вектора 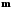 , которая вычисляется по следующей формуле: , которая вычисляется по следующей формуле: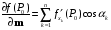 (5.5), (5.5), где 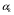 - угол между вектором - угол между вектором 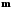 и положительным направлением осей координат. и положительным направлением осей координат.Если же  дифференцируема по каждой из координат в точке дифференцируема по каждой из координат в точке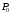 , то вектор , то вектор 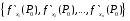 называется градиентом функции называется градиентом функции  в точке в точке 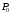 и обозначается символом и обозначается символом 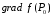 . .Если  дифференцируема в точке дифференцируема в точке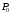 , то в общем случае , то в общем случае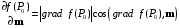 (5.6), (5.6),где справа стоит скалярное произведение. Если при этом 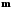 - вектор в касательной плоскости к поверхности уровня - вектор в касательной плоскости к поверхности уровня 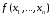 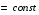 , то , то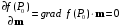 (5.6*) (5.6*)Свойства градиента: 1. Градиент функции  перпендикулярен поверхности уровня перпендикулярен поверхности уровня  . .2. Направление градиента есть направление наиболее быстрого роста функции (т.е. направление наибольшей производной по направлению). Теоремы о дифференцируемых ФМП. Дифференцирование сложной функции. Пусть  дифференцируема в точке дифференцируема в точке 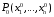 и пусть и пусть 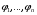 – функции одного переменного, дифференцируемые в точке – функции одного переменного, дифференцируемые в точке 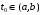 и такие, что и такие, что 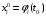 , , 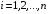 . Тогда сложная функция, составленная из . Тогда сложная функция, составленная из  и и 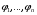 дифференцируема в точке дифференцируема в точке 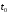 и её производная находится по формуле и её производная находится по формуле 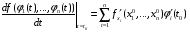 (5.7) (5.7)Дифференцирование неявных функций. Если 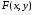 непрерывно дифференцируема в области непрерывно дифференцируема в области 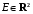 и существует функция и существует функция 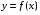 , определенная в , определенная в 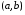 и такая, что для всех и такая, что для всех 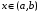 уравнение уравнение 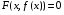 выполняется. А кроме этого выполняется. А кроме этого 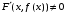 , то , то  дифференцируема в дифференцируема в 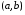 и для каждого и для каждого 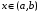 справедливо равенство справедливо равенство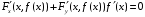 или или 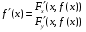 (5.8). (5.8).Формула Тейлора функции двух переменных. Пусть функция  на множестве на множестве 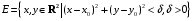 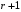 раз дифференцируема. Тогда для всех раз дифференцируема. Тогда для всех 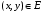 справедлива формула справедлива формула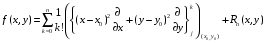 (5.9) (5.9)При этом 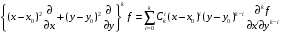 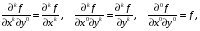 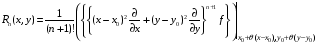 (5.10) (5.10)где 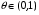 . Величина . Величина 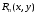 называется остаточным членом (в форме Лагранжа) формулы Тейлора для функции называется остаточным членом (в форме Лагранжа) формулы Тейлора для функции  . .Если при 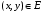 имеет место равенство имеет место равенство 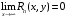 , то можно использовать формулу Тейлора для того, чтобы в некоторой окрестности точки , то можно использовать формулу Тейлора для того, чтобы в некоторой окрестности точки 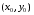 приблизить функцию многочленом приблизить функцию многочленом 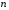 -й степени. Формула Тейлора легко может быть обобщена на функции более чем двух переменных. -й степени. Формула Тейлора легко может быть обобщена на функции более чем двух переменных.Если  дифференцируема в области дифференцируема в области 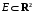 и для всех и для всех 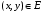 выполнены соотношения выполнены соотношения 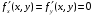 , то , то  - постоянна. - постоянна. |
