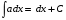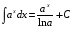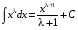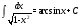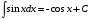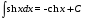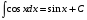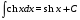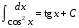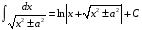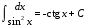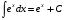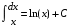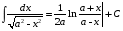Математический анализ для экономистов. Методическое пособие для заочной формы обучения. Выбор темы контрольной работы выбирается по первой букве фамилии студента и последней цифре номера зачетной книжки
 Скачать 2.83 Mb. Скачать 2.83 Mb.
|
|
Дифференциальное исчисление функции двух переменных Задание 1. Для функции двух переменных 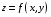 , пользуясь правилами дифференцирования, найти производные: , пользуясь правилами дифференцирования, найти производные: 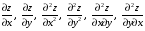 . .
Задание 2.Найти точки экстремума функции 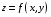 . Характеризовать их тип. . Характеризовать их тип.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ. Неопределенный интеграл Определение и основные свойства неопределенного интеграла Функция 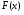 называется первообразной функцией для называется первообразной функцией для 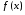 или интегралом для или интегралом для 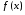 ,если производная от этой функции равна ,если производная от этой функции равна 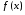 т.е. т.е. 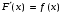 . .Выражение 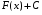 , где , где 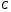 — произвольная постоянная, представляет собой общий вид функции, которая имеет производную — произвольная постоянная, представляет собой общий вид функции, которая имеет производную 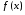 или дифференциал или дифференциал 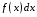 . Это выражение называется неопределенным интегралом и обозначается символом . Это выражение называется неопределенным интегралом и обозначается символом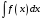 в котором неявным образом уже заключена произвольная постоянная. Произведение 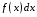 называется подынтегральным выражением, а функция называется подынтегральным выражением, а функция 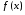 — подынтегральной функцией. — подынтегральной функцией.Из определения неопределенного интеграла непосредственно вытекают следующие свойства: 1. 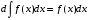 2. 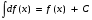 3. Свойство линейности  Таблица простейших интегралов
Приемы интегрирования Замена переменных в неопределенном интеграле Если 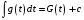 , ,то тогда 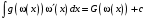 . (4.1) . (4.1)Пусть требуется вычислить интеграл 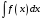 Выбирая в качестве новой переменной функцию 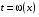 , такую что подынтегральное выражение представляется в виде , такую что подынтегральное выражение представляется в виде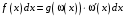 Цель данного приема состоит к переходу более удобной для интегрирования функции 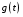 . .Пример. 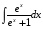 . Вводя . Вводя 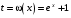 , получаем , получаем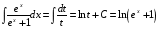 Интегрирование по частям Этот прием представляет сведение данного интеграла 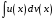 к интегралу к интегралу 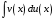 с помощью формулы с помощью формулы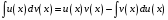 (4.2) (4.2)Этот прием ведет к цели, если 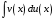 находится легче, чем находится легче, чем 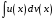 . .Это правило хотя и имеет более ограниченную область применения по сравнению с заменой переменной, существует целый класс функций, который интегрируется именно с помощью этого метода. Сюда можно отнести: 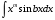 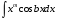 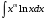 где 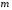 есть любое целое положительное число. есть любое целое положительное число.Применение формулы (4.2) предусматривает последовательное понижение степени 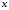 до нулевой. до нулевой.Интегрирование простых дробей К простым дробям относятся 1) 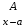 ; 2) ; 2) 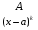 ; 3) ; 3) 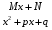 ; 4) ; 4) 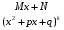 где 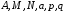 - действительные числа, - действительные числа, 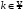 . Кроме того, трехчлен . Кроме того, трехчлен 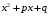 не имеет действительных корней, т.е. не имеет действительных корней, т.е.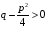 Интегрирование (1) и (2) не представляет трудностей: 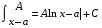 (4.3) (4.3)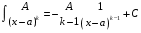 (4.4) (4.4)Для интегрирования дроби (3) применим метод замены переменной. Выделяя сначала из знаменателя полный квадрат 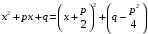 и прибегнув к подстановке 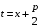 и обозначив 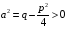 получаем 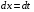 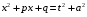 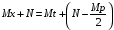 а сам интеграл 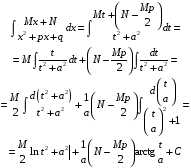 Возвращаясь обратно к переменной 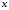 окончательно получаем: окончательно получаем: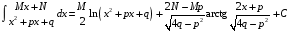 (4.5) (4.5)Для случая (4) подстановка 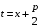 приводит приводит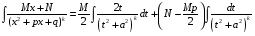 Первый интеграл вычисляется подстановкой 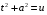 , , 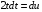 : :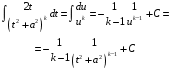 (4.6) (4.6)Второй интеграл вычисляется с помощью рекуррентной формулы 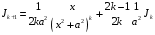 (4.7) (4.7)где 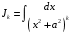 Формула (4.7) позволяет вычислить искомый интеграл для любого натурального индекса 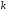 . .Так как при 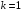 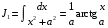 то по формуле (4.7) найдем 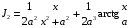 и т.д. и т.д.Интегрирование дробно-рациональных функций Дробно-рациональной функцией (дробью) называется выражение вида 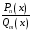 где 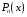 и и 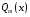 — многочлены степени — многочлены степени 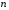 и и 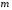 , не имеющие общих корней, т.е. , не имеющие общих корней, т.е.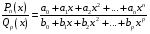 (4.8) (4.8)Дробь (4.8) называется правильной если 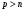 ; неправильной в противном случае. Каждую неправильную дробь можно привести к правильной путем исключения целой части, интегрирование которой не представляет сложностей. ; неправильной в противном случае. Каждую неправильную дробь можно привести к правильной путем исключения целой части, интегрирование которой не представляет сложностей. В курсе высшей алгебры доказывается важная теорема, о том, что любая правильная дробь (4.8) может быть представлена в виде конечного числа правильных дробей. Если 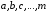 — корни уравнения — корни уравнения 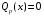 , а , а 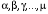 — их соответствующие кратности, так что — их соответствующие кратности, так что 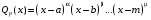 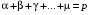 то дробь (4.8) представляется в виде 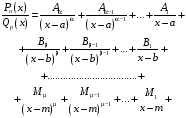 (4.9) (4.9)где числители отдельных дробей определяются из системы линейных уравнений после приведения к общему знаменателю и приравнивания коэффициентов при одинаковых степенях с 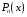 (метод неопределенных коэффициентов). (метод неопределенных коэффициентов).Если 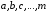 — простые корни уравнения — простые корни уравнения 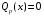 , т.е. , т.е. 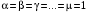 , то , то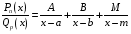 Если некоторые корни уравнения 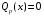 мнимы, то, соединяя вместе элементарные дроби, соответствующие сопряженным корням, можно после некоторых преобразований соответствующие пары дробей представить в виде действительных дробей вида мнимы, то, соединяя вместе элементарные дроби, соответствующие сопряженным корням, можно после некоторых преобразований соответствующие пары дробей представить в виде действительных дробей вида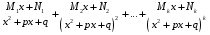 . .и методом неопределенных коэффициентов найти неизвестные 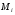 и и 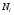 Таким образом, интегрирование правильной рациональной дроби 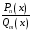 приводится к интегралам вида приводится к интегралам вида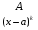 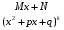 рассмотренных в предыдущем п.3. Интегрирование некоторых выражений, содержащих радикалы Интегралы вида 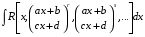 (4.10) (4.10)где 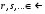 — рациональные числа, приводятся к интегралам от рациональных функций подстановкой — рациональные числа, приводятся к интегралам от рациональных функций подстановкой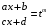 (4.11) (4.11)где 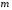 общий знаменатель дробей общий знаменатель дробей 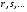 . .Интегралы вида 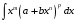 (4.12) (4.12)(интегралы от биномиальных дифференциалов), где 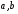 — действительные числа, а — действительные числа, а 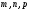 — рациональные, выражаются в элементарных функциях только в следующих случаях: — рациональные, выражаются в элементарных функциях только в следующих случаях:а) когда 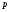 — целое число; тогда этот интеграл имеет вид суммы интегралов (4.10); — целое число; тогда этот интеграл имеет вид суммы интегралов (4.10);б) когда 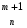 — целое число; подстановкой; подстановкой — целое число; подстановкой; подстановкой 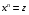 этот интеграл преобразуется к виду (4.10) этот интеграл преобразуется к виду (4.10)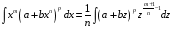 (4.13) (4.13)в) когда 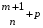 — целое число; при помощи той же подстановки — целое число; при помощи той же подстановки 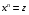 данный интеграл приводится к виду (4.10) данный интеграл приводится к виду (4.10)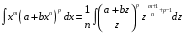 (4.14) (4.14)Рационализация подынтегрального выражения в интегралах вида 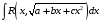 достигается с помощью, по крайней мере, одной из следующих трех подстановок, называемых подстановками Эйлера а) 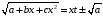 при при 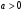 ; ;б) 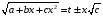 при при 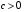 ; ;в) 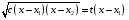 при условии, что корни при условии, что корни 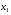 и и 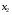 уравнения уравнения 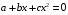 действительны. действительны.Интегрирование тригонометрических выражений Интегралы вида 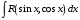 (4.14) (4.14)могут быть всегда приведены к интегралам от рациональных функций при помощи подстановки 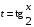 (4.15) (4.15)При этом функции подынтегрального выражения выражаются через новые переменные 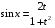 ; ; 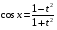 ; ; 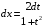 (4.16) (4.16)Если при этом подынтегральная функция 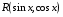 удовлетворяет соотношению удовлетворяет соотношению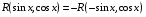 (4.17) (4.17)то выгодно применить подстановку 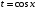 . Например, с помощью этой подстановки интеграл . Например, с помощью этой подстановки интеграл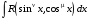 (4.18) (4.18)где 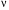 — нечетное число, а — нечетное число, а 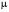 — четное, с соответствующей заменой — четное, с соответствующей заменой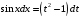 (4.19) (4.19)приводится к интегралу от рациональной функции. Если эта функция удовлетворяет соотношению 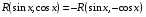 (4.20) (4.20)то выгодно применить подстановку 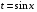 . Например, с помощью этой подстановки интеграл . Например, с помощью этой подстановки интеграл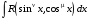 (4.21) (4.21)где 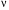 — четное число, а — четное число, а 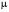 — нечетное, с соответствующей заменой — нечетное, с соответствующей заменой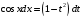 (4.22) (4.22)приводится к интегралу от рациональной функции. Если эта функция удовлетворяет соотношению 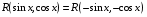 (4.23) (4.23)то выгодно применить подстановку 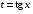 . Например, с помощью этой подстановки интеграл . Например, с помощью этой подстановки интеграл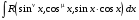 (4.24) (4.24)где 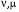 — четные числа, с соответствующей заменой — четные числа, с соответствующей заменой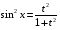 ; ; 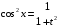 ; ;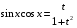 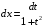 (4.25) (4.25)приводится к интегралу от рациональной функции. Интегрирование выражений, содержащих гиперболические функции Интегралы вида 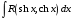 (4.26) (4.26)могут быть всегда приведены к интегралам от рациональных функций при помощи подстановки 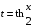 (4.27) (4.27)При этом функции подынтегрального выражения выражаются через новые переменные 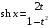 ; ; 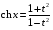 ; ; 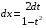 (4.22) (4.22) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

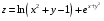
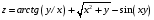 1
1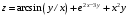
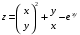 3
3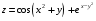
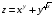 5
5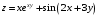
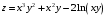 7
7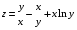
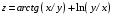 9
9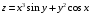
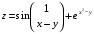 11
11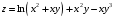
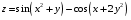 13
13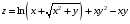
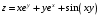 15
15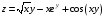
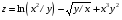 17
17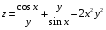
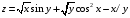 19
19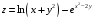
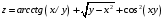 21
21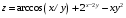
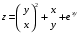 23
23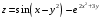
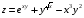 25
25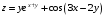
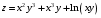 27
27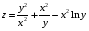
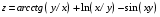 29
29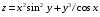
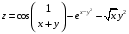 31
31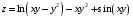
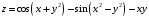 33
33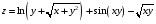
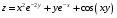 35
35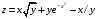
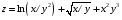 37
37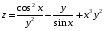
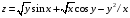 39
39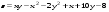
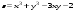 1
1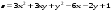
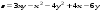 3
3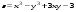
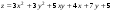 5
5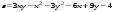
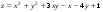 7
7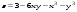
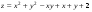 9
9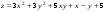
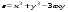
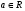 11
11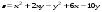
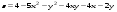 13
13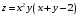
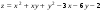 15
15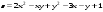
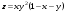 17
17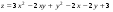
 19
19
 21
21
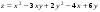 23
23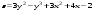
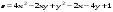 25
25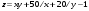
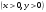
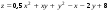 27
27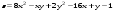
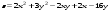 29
29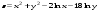
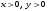
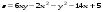 31
31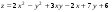
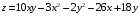 33
33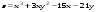
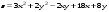 35
35