Математический анализ для экономистов. Методическое пособие для заочной формы обучения. Выбор темы контрольной работы выбирается по первой букве фамилии студента и последней цифре номера зачетной книжки
 Скачать 2.83 Mb. Скачать 2.83 Mb.
|
|
Экстремумы ФМП. Пусть функция  определена в некоторой области определена в некоторой области 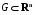 и и 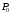 - точка в - точка в 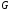 . Значение функции . Значение функции  в данной точке называется минимумом (локальным минимумом) функции в данной точке называется минимумом (локальным минимумом) функции  в в 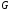 , если существует окрестность точки , если существует окрестность точки 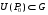 точки точки 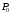 , такая что для всех точек , такая что для всех точек 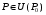 \ \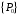 выполняется неравенство выполняется неравенство 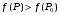 . Аналогично максимумом (локальным максимумом) функции . Аналогично максимумом (локальным максимумом) функции  в в 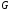 , если , если  . Если неравенства строгие, то локальным максимумом (минимум) называют строгим, в противном случае – нестрогим. Максимум или минимум также называют экстремумом ( локальным экстремумом) функции . Если неравенства строгие, то локальным максимумом (минимум) называют строгим, в противном случае – нестрогим. Максимум или минимум также называют экстремумом ( локальным экстремумом) функции  в в 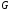 . . Необходимые условия существования экстремума. Если 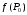 - экстремум функции - экстремум функции  , дифференцируемой по каждой из координатв некоторой окрестности , дифференцируемой по каждой из координатв некоторой окрестности 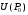 точки точки 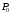 , то выполняются равенства , то выполняются равенства 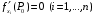 . .Достаточные условия существования экстремума. Пусть функция  дважды непрерывно дифференцируема в дважды непрерывно дифференцируема в 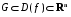 и в точке и в точке 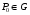 выполняются равенства выполняются равенства 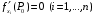 . Если, кроме того, положительно (или отрицательно) определена квадратичная форма . Если, кроме того, положительно (или отрицательно) определена квадратичная форма 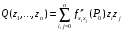 (5.11) (5.11)то функция  имеет минимум (или максимум) в точке имеет минимум (или максимум) в точке 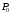 , а если форма , а если форма 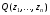 неопределенная, то функция неопределенная, то функция  не имеет экстремума в точке не имеет экстремума в точке 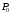 и точка в этом случае называется седловой точкой функции и точка в этом случае называется седловой точкой функции  . .Нахождение условных экстремумов (метод неопределенных множителей Лагранжа). Общая постановка задачи: Найти все экстремумы и наибольшее, а также наименьшее значения функции 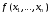 , определенной в области , определенной в области 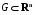 , для точек , для точек 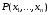 , удовлетворяющих дополнительным условиям: , удовлетворяющих дополнительным условиям: 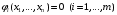 (5.12) (5.12)где 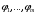 - действительные функции, определенные в - действительные функции, определенные в 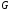 . .Необходимые условия существования условного экстремума. Пусть функции 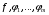 непрерывно дифференцируемы в непрерывно дифференцируемы в 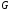 и ранг функциональной матрицы и ранг функциональной матрицы  . Положим, что . Положим, что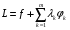 (5.13) (5.13)(функция 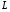 является функцией Лагранжа с множителями является функцией Лагранжа с множителями 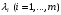 - произвольные действительные числа). Если - произвольные действительные числа). Если  в точке в точке 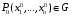 при дополнительных условиях (5.14) имеет экстремум, то справедливы соотношения: при дополнительных условиях (5.14) имеет экстремум, то справедливы соотношения:а) 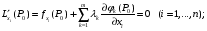 (5.14) (5.14)б) 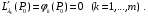 Таким образом, необходимым условием существования условного экстремума функции  в точке в точке  при дополнительных условиях при дополнительных условиях  являются следующие являются следующие 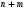 уравнений с уравнений с 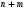 количеством переменных количеством переменных 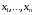 и и 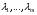 : :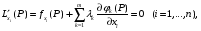 (5.15) (5.15)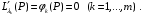 Примеры Задача №1: Найти частные производные для функции 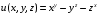 . .Решение: 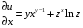 , ,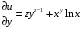 , , 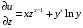 . .Задача №2: Найти 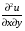 , если , если 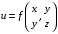 . .Решение: 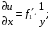 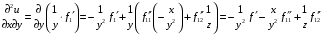 . .Задача №4: Исследовать на экстремумы функцию 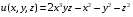 . .Решение: Координаты  критической точки вследствие гладкости функции должны удовлетворять системе критической точки вследствие гладкости функции должны удовлетворять системе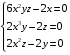 или или 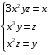 Из системы уравнений получим пять критических точек: 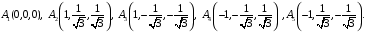 Так как 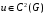 для любой области для любой области 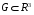 , то возможно дальнейшее исследование поведения функции , то возможно дальнейшее исследование поведения функции 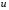 в стационарных точках с помощью достаточного условия экстремума: в стационарных точках с помощью достаточного условия экстремума: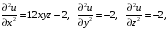 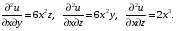 Отсюда получим, что в точке 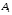 : : 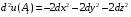 . Так как этот является ни чем иным как отрицательно определенной квадратичной формой (5.11), то можно сделать вывод что в точке . Так как этот является ни чем иным как отрицательно определенной квадратичной формой (5.11), то можно сделать вывод что в точке 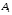 функция функция 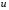 имеет строгий локальный максимум. имеет строгий локальный максимум.Рассмотрим точку 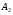 : : 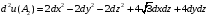 . .Для анализа запишем матрицу этой квадратичной формы и применим критерий Сильвестра. 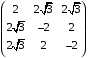 Выпишем главные миноры: 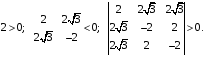 Распределение знаков миноров показывает, что данная квадратичная форма знакопеременная, таким образом в точке 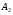 функция функция 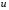 не имеет экстремума, то есть не имеет экстремума, то есть 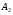 - седловая точка функции - седловая точка функции 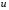 . .Аналогичным образом определяется, что и точки 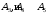 также являются Седловыми точками функции также являются Седловыми точками функции 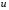 . .Задача №5: Исследовать на экстремумы функцию 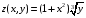 . .Решение: Имеем, что 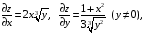 следовательно ни одна точка вне оси следовательно ни одна точка вне оси 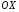 не будет критической. не будет критической. Пусть 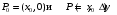 , тогда , тогда 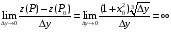 Таким образом, все точки оси 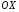 являются критическими точками функции являются критическими точками функции  , в которых , в которых 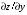 не существует. Из определения не существует. Из определения 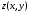 получаем, что если получаем, что если 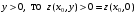 , если же , если же 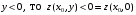 для любого для любого 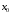 . Итак, получается, что каждая точка на оси . Итак, получается, что каждая точка на оси 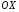 является критической точкой функции является критической точкой функции  , и в каждой из них нарушены условия гладкости и эти точки, следовательно, являются седловыми точками функции , и в каждой из них нарушены условия гладкости и эти точки, следовательно, являются седловыми точками функции  . .Замечание: Из примера видно, что если в критической точке функция может не иметь даже хотя бы одной частной производной, и, следовательно, эта точка может быть равновероятно точкой локального минимума, локального максимума или седловой точкой. Задача №6: Исследовать на экстремумы функцию 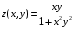 . .Решение: 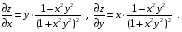 Отсюда делаем вывод, что критическими точками функции  будут будут 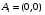 и все другие и все другие 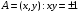 . Из неравенства . Из неравенства 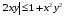 получаем, что получаем, что 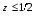 . В каждой точке линии . В каждой точке линии 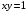 имеем, что имеем, что 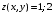 , а также, если , а также, если 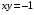 , то , то 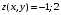 . Таким образом можно утверждать, что в каждой точке . Таким образом можно утверждать, что в каждой точке 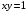 функция имеет нестрогий максимум, а в функция имеет нестрогий максимум, а в 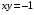 - нестрогий минимум. Найдем вторые частные производные функции - нестрогий минимум. Найдем вторые частные производные функции  . .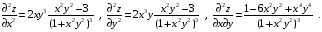 Если 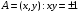 , то квадратичная форма , то квадратичная форма 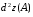 полуопределена, как и должно быть в точках нестрогого экстремума: полуопределена, как и должно быть в точках нестрогого экстремума: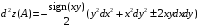 . .А для точки 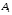 квадратичная форма квадратичная форма 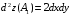 - знакопеременная, следовательно, - знакопеременная, следовательно, 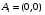 - седловая точка функции - седловая точка функции  . .Задача №7: Найти точки условного экстремума функции 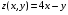 , если , если 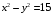 . .Решение: В этом задании 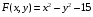 , матрица , матрица 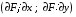 есть есть 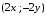 . Из условия . Из условия 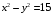 следует, что все точки, удовлетворяющие данному условию, имеют ненулевые координаты, а значит и минор следует, что все точки, удовлетворяющие данному условию, имеют ненулевые координаты, а значит и минор 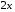 матрицы матрицы 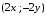 также отличен от нуля. Поэтому условие определяет на этом множестве функцию также отличен от нуля. Поэтому условие определяет на этом множестве функцию 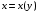 . .А теперь мы рассматриваем функцию  , как функцию одного аргумента , как функцию одного аргумента 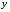 : : 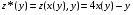 . Из условия получаем, что . Из условия получаем, что 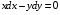 откуда откуда 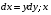 , подставляя, получим , подставляя, получим 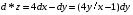 . В итоге для координат критической точки функции . В итоге для координат критической точки функции 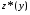 имеем систему уравнений: имеем систему уравнений: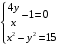 Решая систему, получим, что возможными точками локального экстремума могут быть точки 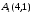 и и 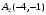 . .Теперь рассмотрим 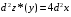 в этих точках, из условия имеем в этих точках, из условия имеем 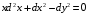 . Тогда для . Тогда для 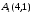 имеем имеем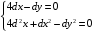 , ,откуда получим, что 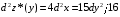 и точка и точка 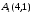 является точкой локального условного минимума функции является точкой локального условного минимума функции 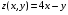 при условии при условии 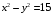 , причем , причем 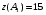 . .Точно также получим, что в точке 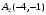 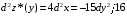 , то есть эта точка является локальным условным максимумом функции , то есть эта точка является локальным условным максимумом функции 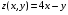 при условии при условии 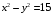 , причем , причем 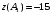 . .Задача №8: Найдем экстремальные значения функции 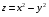 на прямой на прямой 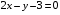 . .Решение: Запишем функцию Лагранжа 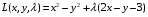 Координаты критических точек функции 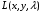 находятся из системы находятся из системы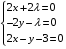  отсюда получаем 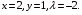 В точке (2,1,-2) выражение В точке (2,1,-2) выражение 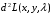 ,равное ,равное 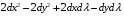 , есть знакопеременная квадратичная форма, следовательно, точка (2,1,-2) не экстремальная точка функции , есть знакопеременная квадратичная форма, следовательно, точка (2,1,-2) не экстремальная точка функции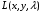 ,но эта точка может быть экстремальной точкой функции ,но эта точка может быть экстремальной точкой функции 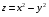 при условии связи. В самом деле, из условия связи имеем при условии связи. В самом деле, из условия связи имеем 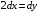 . Учитывая это соотношение, для . Учитывая это соотношение, для 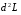 получаем выражение получаем выражение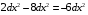 ,которое есть отрицательно определенная квадратичная форма, и, следовательно, точка (2,1) является точкой локального максимума функции ,которое есть отрицательно определенная квадратичная форма, и, следовательно, точка (2,1) является точкой локального максимума функции 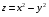 при условии связи при условии связи 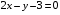 ВОПРОСЫ К ЭКЗАМЕНУ.
Литература Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. С.-Пт. “Лань”, 2006 год. 736 с. Высшая математика для экономических специальностей. Учебник и практикум / под. ред. Кремера Н.Ш. Части 1,2. М.: Высшее образование, 2005 год. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1 - М.: Высш. шк., 1980. Зайцев И.А. Высшая математика. М.: Наука. 2003 год. Ильин В.А. Куркина А.В. Высшая математика. М.: ТКВелби. 2005 год. 600 с. Ильин В.А., Куркина А.В. Высшая математика. – М.: Изд. МГУ, 2005. Крамер Н.И., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов. – М.: Юнити, 2000. Красс М.С., Чупрынов Б.П. Математика для экономистов. Учебное пособие. СПб.: Питер, 2006. – 464 с. Кремер Н.Ш. Высшая математика для экономистов. — М.: ЮНИТИ, 2003. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты. С.-Пт.: “Лань”, 2005 год. 240 с. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1987. Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 1, 2. М.: Наука, 1978. Сборник задач по курсу высшей математики / Под ред. Кручковича Г.И. М.: Высшая школа, 1973. – 576 с. Сборник задач по математике для втузов. Часть 1. Линейная алгебра и основы математического анализа. /Под ред. Ефимова А.В., Демидовича Б.П. М.: Наука, 1986. – 464 с. Смирнов В.И. Курс высшей математики. — М.: Наука, 1977. Шипачев В.С. Основы высшей математики. — М.: Высшая школа, 1989. |

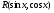 с помощью универсальной тригонометрической подстановки.
с помощью универсальной тригонометрической подстановки.