Информатика (методичка). Методическое пособие основы алгоритмизации

• Название: Методическое пособие основы алгоритмизации
• Анкор: Информатика (методичка).doc
• Дата: 03.04.2018
• Размер: 1.36 Mb.
• Имя файла: Информатика (методичка).doc
• Тип: Методическое пособие; #17580
• страница: 2 из 8

2. АЛГОРИТМЫ ЛИНЕЙНОЙ СТРУКТУРЫ

В 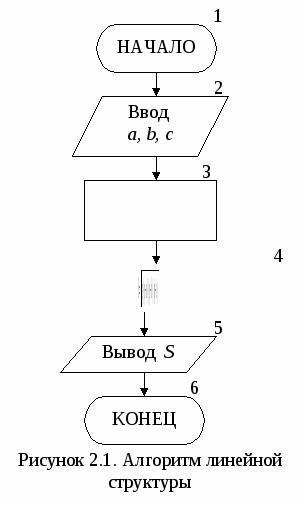линейном вычислительном процессе все действия выполняются в строгой последовательности друг за другом. Таким образом, существует только один путь, по которому можно пройти из блока «Начало» в блок «Конец» алгоритма, т.е. выполнить алгоритм.

Пример. Составить алгоритм вычисления площади треугольника с заданными сторонами a, b и с.

Как известно из курса геометрии площадь треугольника, заданного длинами сторон, можно вычислить, используя формулу Герона. Разрабатываемый алгоритм (рис. 2.1) должен обеспечивать ввод исходных данных, т.е. значений длин сторон треугольника a, b и с (блок 2). Затем, используя введенные значения, вычислять полупериметр Р (блок 3) и значение площади треугольника S (блок 4). После завершения вычислений необходимо вывести результат, т.е. полученное значение площади треугольника S (блок 5).

Однако решение абсолютного большинства инженерных задач невозможно свести к алгоритмам линейной структуры.

3. АЛГОРИТМЫ РАЗВЕТВЛЯЮЩЕЙСЯ СТРУКТУРЫ

Р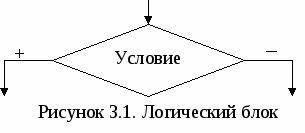азветвляющийся вычислительный процесс позволяет выбрать один из нескольких вариантов решения поставленной задачи в зависимости от выполнения некоторых условий. Таким образом, существует несколько различных путей, по которым можно пройти из блока «Начало» в блок «Конец» алгоритма, т.е. выполнить алгоритм.

Для реализации процесса выбора одного из двух вариантов решения используется логический блок (блок проверки условий), приведенный на рисунке 3.1. При входе в этот блок выполняется проверка логического условия (обычно математического неравенства). Если результат проверки условия «Истина», т.е. условие выполняется, то происходит переход к выполнению блоков, стоящих по ветви «+». В противном случае, т.е. когда проверяемое условие не выполняется, происходит переход к выполнению блоков, стоящих по ветви «–».

Е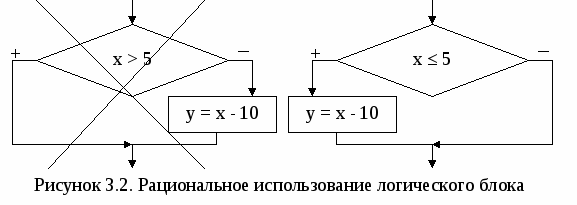
сли требуется выбрать один из трех и более вариантов решения, то необходимо использовать вложенные логические блоки. В случае, когда действия должны выполняться только по одной из ветвей логического блока, их необходимо реализовывать по ветви «+», подобрав соответствующее условие (рис. 3.2).

При выполнении вычислений необходимо учитывать область определения математических функций. Следовательно, вначале необходимо проверить возможность вычисления данного математического выражения при текущих значениях исходных данных, т.е. проверить «аномалию». К наиболее часто встречающимся «аномалиям» относятся: операция деления (на 0 делить нельзя), вычисление квадратного корня (подкоренное выражение должно быть ≥ 0), вычисление логарифма (выражение под знаком логарифма должно быть > 0), вычисление tg, ctg. В случае возникновения «аномалии» (невозможно выполнить вычисления) необходимо пропустить все действия, которые зависят от вычисляемой величины, и перейти в ту часть алгоритма, где можно продолжить вычисления.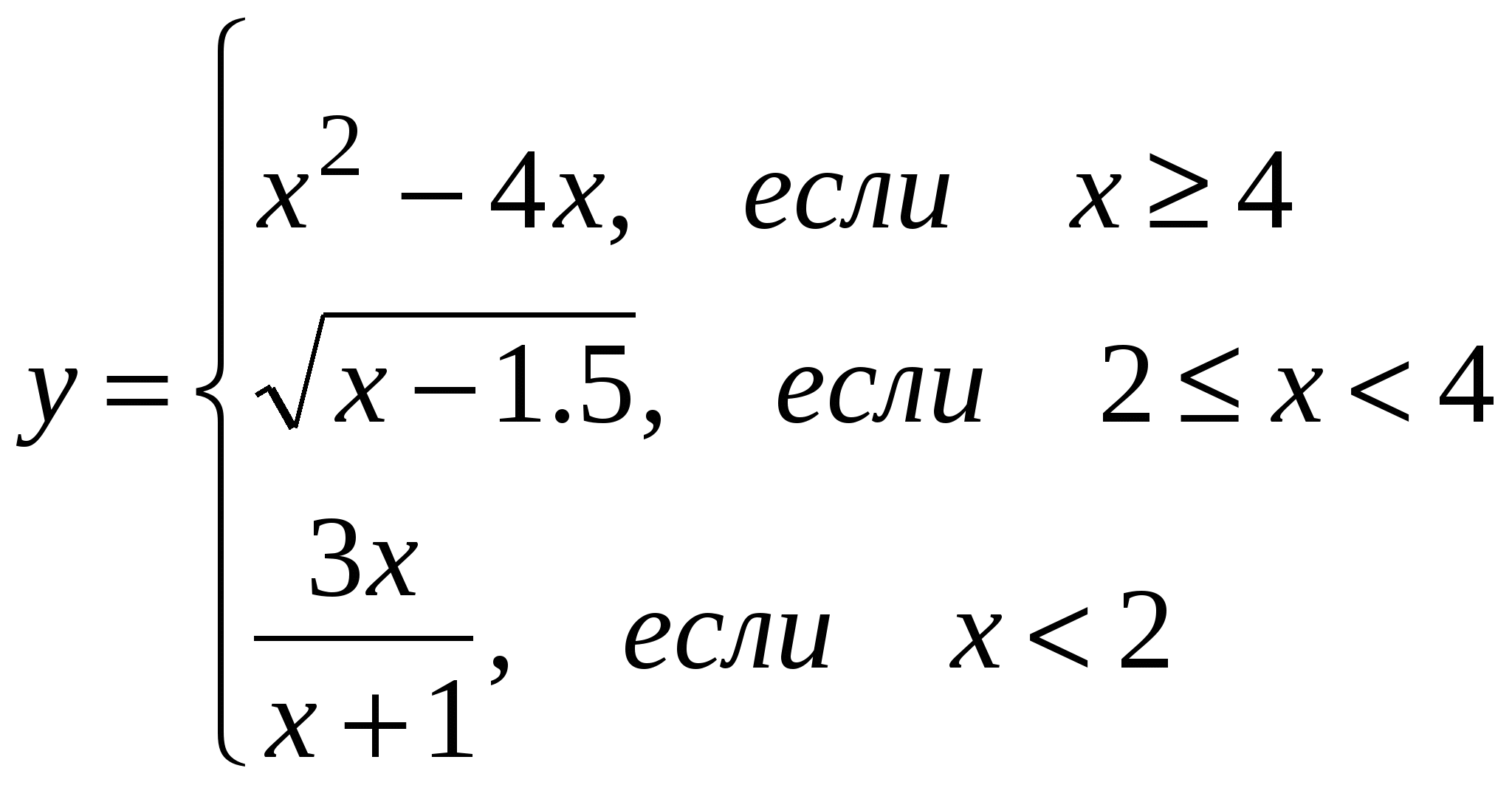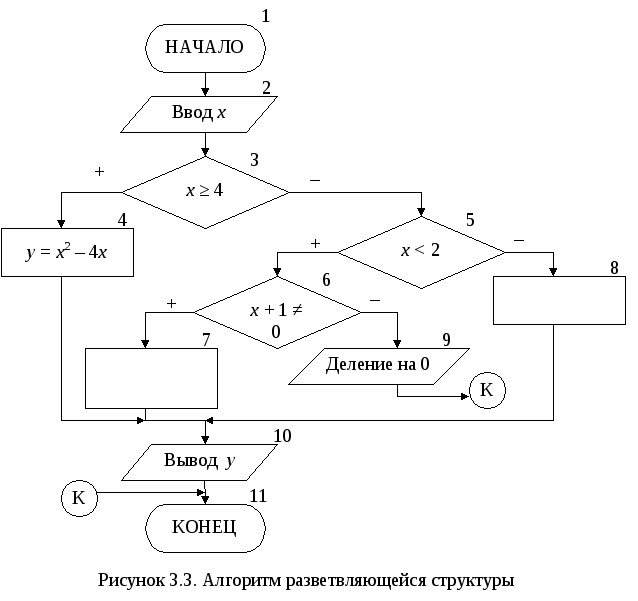


Пример. Составить блок-схему алгоритма, вычисляющего значение у по одной из трех формул, в зависимости от значения х. Блок-схема алгоритма приведена на рисунке 3.3.

Для выбора формул, по которым будет вычисляться значение у, необходимо проверить три условия. Такие ограничения являются взаимоисключающими условиями и достаточно проверить только два условия, т.е. если не выполняются два условия, то третье выполняется автоматически и его не надо проверять.

Исходными данными для решения поставленной задачи является значение х, которое вводится в блоке 2. Затем в блоке 3 проверяется 1-е ограничение (х≥4), в случае его выполнения происходит переход к блоку 4, в котором вычисляется значение у по 1-й формуле. Если результатом проверки 1-го условия является «ЛОЖЬ» (это означает, что х < 4), то необходимо проверить одно из двух оставшихся условий. Обычно выбирается более «короткое» ограничение (в блоке 5 проверяется 3-е ограничение). Если х < 2, то необходимо вычислять y по 3-й формуле, в которой может возникнуть «аномалия» – деление на 0, поэтому в блоке 6 проверяется неравенство знаменателя дроби нулю. И только после этого в блоке 7 вычисляется значение у. В том случае, когда невозможно вычислить значение у по 3-й формуле, выводится сообщение о возникновении ошибки (блок 9) и выполняется переход на конец алгоритма. И, наконец, если значение х не удовлетворяет ни 1-му, ни 3-му ограничению, значит, выполняется 2-е ограничение и у вычисляется по 2-й формуле (блок 8). Эта формула также содержит «аномалию» – подкоренное выражение должно быть ≥ 0. Однако, проверять её не надо, так как при любом значении х, попадающем в интервал [2; 4[, подкоренное выражение всегда > 0. Не зависимо от того, по какой формуле будет вычислено значение у его надо вывести на экран, поэтому выходы блоков 4, 7 и 8 объединяются и происходит переход к блоку 10, в котором выводится у.

За одно выполнение алгоритма может быть вычислено только одно значение у в зависимости от введенного значения х. Всего же существует 4 варианта работы алгоритма в зависимости от значения х. При этом если возникнет «аномалия», у вычислен не будет.