Информатика (методичка). Методическое пособие основы алгоритмизации

• Название: Методическое пособие основы алгоритмизации
• Анкор: Информатика (методичка).doc
• Дата: 03.04.2018
• Размер: 1.36 Mb.
• Имя файла: Информатика (методичка).doc
• Тип: Методическое пособие; #17580
• страница: 4 из 8

5. АЛГОРИТМЫ ОБРАБОТКИ ОДНОМЕРНЫХ МАССИВОВ

Массив – это последовательность однотипных элементов, каждый из которых имеет одно и тоже имя, но однозначно определяется своим номером (индексом). Массив – это не скалярная величина, а структурированный тип данных.

Обычно используются одномерные (вектор) и двумерные (матрица) массивы. В одномерном массиве каждый элемент имеет один индекс, определяющий положение элемента в массиве. В двумерном массиве каждый элемент имеет два индекса. Чаще всего нумерация индексов начинается с 1, но может и с 0.

	X1	X2	X3	…	XN
Значение элемента	2	0	1	…	7
Индекс элемента i	1	2	3	…	N

Основными характеристиками массива являются:

– размерность, т.е. количество элементов (обычно обозначается N);

– значения элементов (например, X₁ = 2; X₃ = 1 и т.д.).

Обработка массива обычно заключается в последовательном переборе его элементов и выполнении над ними однотипных операций, т.е. обработка массива является циклическим вычислительным процессом. Для этого достаточно организовать цикл по перебору индексов элементов массива. Наиболее рационально для этой цели использовать цикл «Для» на основе блока модификации (рис. 5.1).

При входе в блок модификации (рис. 5.1.а,б, линия 1) автоматически выполняются следующие действия. Параметру цикла i присваивается начальное значение inи проверяется, не превышает ли оно конечного значения ik. Если результатом проверки условия является истина, то происходит переход к выполнению тела цикла (линия 2). После этого осуществляется возврат в блок модификации (линия 3), увеличение параметра цикла i на значение шага hi и проверка условия продолжения цикла и т.д. Когда текущее значение параметра цикла i превысит конечное значение ik, цикл завершит свою работу (линия 4). Если шаг изменения параметра цикла hi равен 1, то его в блоке модификации можно не указывать (рис. 5.1,в).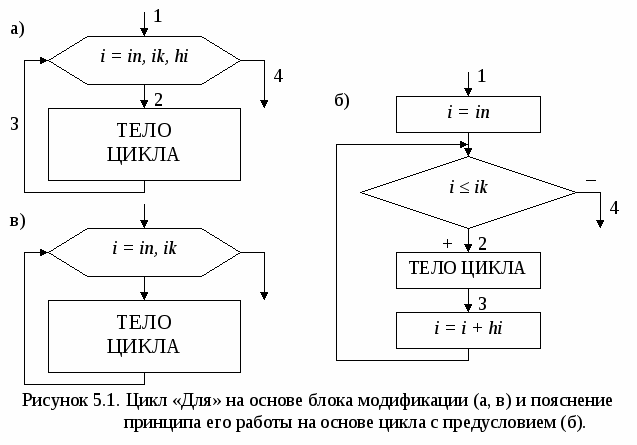



В одних языках программирования, таких как Турбо Паскаль, Delphi, существуют ограничения на использование цикла «Для» (параметр цикла, его начальное и конечное значения должны быть только целочисленного типа; шаг изменения может быть равен только 1 или -1). В других языках программирования, таких как Си, Visual Basic, этих ограничений нет. Но в любом случае цикл «Для» идеально подходит для организации обработки массивов.
5.1. Ввод и вывод элементов одномерного массива
Ввод элементов массива выполняется в два этапа. Вначале указывается его размерность (количество элементов), а затем задаются значения для каждого элемента массива. Рассмотрим два способа организации ввода элементов одномерного массива.

1 способ. Алгоритм ввода массива Х размерностью N (i=1N) (рис. 5.1.1.а). На первом этапе вводится размерность массива N (блок 1). На втором этапе организовывается цикл «Для» на основе блока модификации, выполняющий поэлементный ввод произвольных однотипных значений компонент массива.

Параметр цикла i в тоже время является индексом элементов массива Х. Блок модификации (блок 2) перебирает значения i от 1 до Nи для каждого значения i выполняется ввод значения для Х_i-го элемента массива (блок 3), т.е. при i=1 будет введено значение для X₁, при i=2 – для X₂ и т.д. Таким образом, за один шаг выполнения цикла вводится один элемент массива Х.

2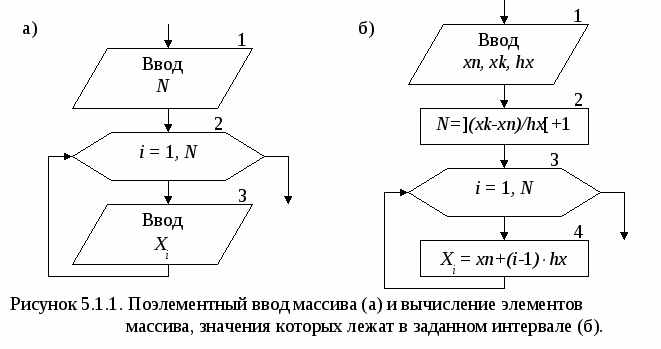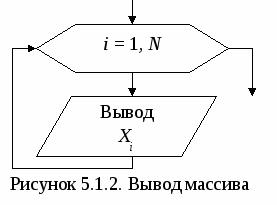
способ. Алгоритм формирования массива Х, значения элементов которого принадлежат заданному интервалу xn ≤ X_i≤ xk с шагом изменения hx (рис. 5.1.1.б). На первом этапе вводятся значения xn, xk и hx (блок 1) и вычисляется N – размерность массива X (блок 2). На втором этапе организовывается цикл «Для» на основе блока модификации (блок 3), в котором перебираются значения i. На каждом шаге цикла вычисляется значение одного элемента массива Х (блок 4), т.е. при i=1 будет вычислено значение для X₁=xn+(1-1)hx=xn, при i=2 – для X₂= =xn+(2-1)hx=xn+hx и т.д.

Вывод массива также выполняется поэлементно с помощью цикла «Для» (рис. 5.1.2).

Циклы по вводу или выводу элементов массивов не обязательно делать отдельно. Их можно объединять с циклами по обработке элементов массивов.

Пример 5.1. Используя элементы исходного массива Х размерности N, вычислить элементы массива Y по следующей формуле: Y_i=1/X_i. Определить среднее арифметическое положительных элементов массива Y.

Результирующий массив Y будет иметь туже размерность, что и массив Х.

Решение поставленной задачи можно разделить на 4 этапа: ввод элементов исходного массива Х, вычисление элементов массива Y, вычисление среднего арифметического положительных элементов массива Y и вывод элементов массива Y. Для реализации каждого этапа необходимо организовать отдельные циклы для перебора элементов массивов. Однако, такой способ решения не рационален, хотя и возможен. Вследствие того, что организация всех четырех циклов будет полностью идентична, этапы решения со 2-го по 4-й можно реализовать с помощью только одного цикла «Для». Это значительно уменьшит размер алгоритма и скорость его выполнения. Блок-схема алгоритма приведена на рис. 5.1.3.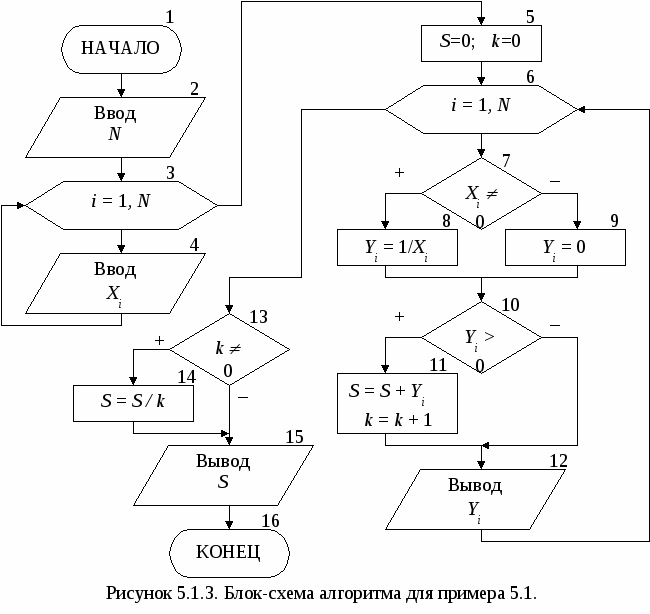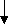




Ввод исходного массива (блоки 2-4) осуществляется поэлементно, описанным выше способом. В блоке 5 присваиваются начальные значения для переменных S и k (сумма и количество положительных элементов массива Y). Затем организовывается цикл «Для» (блок 6), на каждом шаге которого будут выполняться следующие действия: вычисление по заданной формуле текущего элемента массива Y (блоки 7-9); проверка – не является ли вычисленный элемент Y_i положительным (блок 10); добавление положительного значения Y_i к сумме S и увеличение счетчика таких элементов k на 1 (блок 11); вывод текущего элемента массива Y (блок 12).

Особое внимание следует обратить на наличие возможной «аномалии» в вычисляемом выражении (X_i не должно быть равным 0). Обработка «аномалий», возникающих при вычислении элементов массива, немного отличается от предложенной в п. 4.1. Если просто пропустить все операции, которые невозможно выполнить, то текущий элемент массива не будет вычислен. В результате может быть сформирован массив, у которого часть элементов будет не определено (массив с «дырами»). Дальнейшее использование такого массива недопустимо. Поэтому в случае возникновения аномалии при вычислении текущего элемента массива, ему надо присвоить такое значение, которое не повлияет на дальнейшие вычисления, например 0 (блок 9).

Таким образом, с помощью одного цикла «Для» будут поочередно перебраны все элементы массива Х, для каждого элемента X_i вычислен и выведен соответствующий элемент массива Y_i. После выхода из цикла вычисляется и выводится среднее арифметическое значение положительных элементов массива Y (блоки 13-15). При этом предварительно в блоке 13 проверяется возможность деления на ноль.
5.2. Нахождение максимального и минимального

элементов массива
Принцип поиска максимального или минимального элемента массива заключается в следующем: в дополнительную переменную заносится значение первого элемента массива, которое принимается за максимум (минимум); затем организовывается перебор оставшихся элементов массива, каждый из которых сравнивается с максимумом (минимумом); если текущий элемент массива оказывается больше (меньше), чем принятый за максимум (минимум), то этот элемент становится максимальным (минимальным). Таким образом, после завершения перебора элементов массива в дополнительной переменной окажется максимальное (минимальное) значение среди элементов массива. Фрагмент блок-схемы алгоритма, реализующий описанный метод приведен на рисунке 5.2.1.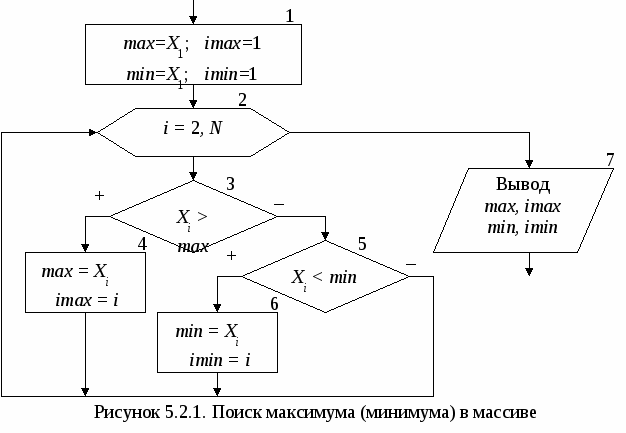



В блоке 1 дополнительным переменным max и min, в которых будут храниться максимальное и минимальное значения соответственно, присваивается значение 1-го элемента массива. Кроме этого введены еще две переменные imax и imin, которые будут использоваться для хранения номеров максимального и минимального элементов массива. С помощью блока модификации (блок 2) организовывается цикл по перебору элементов массива Х (перебор начинается со 2-го элемента, так как 1-й элемент уже обработан в блоке 1). Если текущий элемент массива X_i больше значения, которое хранится в переменной max (блок 3), то за максимум принимается значение этого элемента: max=X_i, и запоминается его номер: imax=i (блок 4). Если текущий элемент массива не больше максимума, то проверяется, не меньше ли он минимума (блок 5). В случае если текущий элемент X_i окажется меньше минимального значения, которое хранится в переменной min, то за минимум принимается значение этого элемента: min=X_i, и запоминается его номер: imin=i (блок 6). После выхода из цикла будут выведены значения максимального и минимального элементов, а также их номера в массиве (блок 7).

П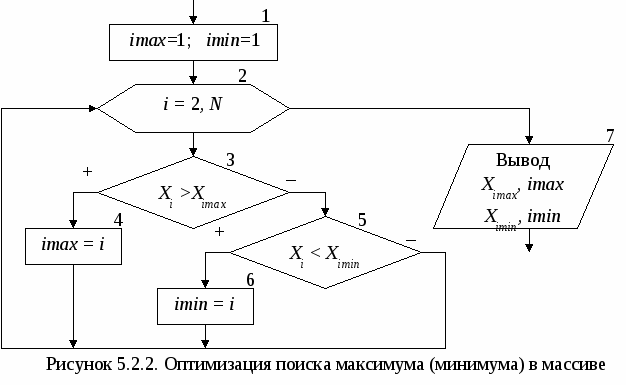риведенный выше алгоритм имеет один недостаток – в нем используется две лишние переменные max и min. Зная индекс элемента массива всегда можно получить его значение, поэтому нет необходимости хранить максимальное и минимальное значения в отдельных переменных. Оптимальный алгоритм приведен на рис. 5.2.2.

В блоке 1 дополнительным переменным imax и imin, используемых для хранения номеров максимального и минимального элемента, присваивается значение 1. Таким образом, за максимум и минимум принимается 1-й элемент массива, само же значение этого элемента нигде дополнительно не сохраняется. Оставшиеся элементы массива также перебираются, начиная со второго (блок 2). При этом каждый элемент массива X_i сравнивается с элементами, имеющими номер равный imax (блок 3) и imin (блок 6), т.е. с элементами принятыми за максимум (минимум). Если результат проверки условий является истиной, то в переменных imax и imin сохраняются индексы новых максимального (блок 4) и минимального (блок 6) элементов. После выхода из цикла будут выведены значения максимального и минимального элементов, а также их номера в массиве (блок 7).

Если в массиве имеется несколько элементов равных по значению максимальному (минимальному) элементу, то алгоритмы, приведенные на рис 5.2.1 и 5.2.2, определят позицию только первого такого элемента. Например, чтобы найти количество элементов массива равных максимальному и позицию последнего такого элемента, можно воспользоваться алгоритмом, приведенным на рис. 5.2.3.

В начале алгоритма за максимум принимается 1-й элемент массива и вводится переменная k для подсчета количества элементов равных максимальному (блок 1). Затем организовывается цикл по перебору оставшихся элементов массива (блок 2). На каждом шаге цикла выполняется следующая последовательность действий.




Вначале текущий элемент массива X_i сравнивается с максимальным (блок 3). Если он оказывается больше элемента, принятого за максимальный, то запоминается номер этого элемента и переменной k присваивается 1 (блок 4). Это означает, что встретился первый «новый» максимальный элемент.

Если текущий элемент не больше максимума, значит, он может быть равным или меньше максимального элемента. Поэтому в блоке 5 текущий элемент массива X_iпроверяется на равенство максимальному. Если он оказывается равным максимуму, то опять запоминается номер текущего элемента и значение переменной k увеличивается на 1 (блок 6). Это означает, что встретился следующий элемент равный максимальному элементу. В итоге после выхода из цикла в переменной imax будет храниться индекс последнего по счету элемента равного максимальному, а в переменной k количество элементов, равных максимуму. Если же из блока 6 убрать операцию imax=i, то в переменной imax, как и в предыдущих примерах будет сохранен номер первого по счету элемента равного максимальному.

В некоторых задачах невозможно вначале принять за максимум (минимум) первый элемент массива. Например, если элементы массива ещё не определены (не введены или не вычислены), или если необходимо найти максимум (минимум) только среди положительных, четных по значению и т.д. элементов. Во втором случае неизвестно когда в массиве встретится первый такой элемент. В таких ситуациях можно использовать способ, реализованный в алгоритме из примера 5.2.

Пример 5.2. В массиве Х [N] найти минимальный положительный элемент.

М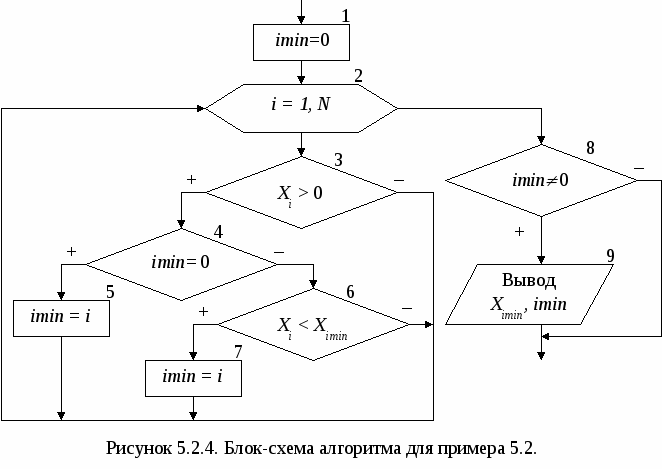ассив Х может содержать как положительные, так и отрицательные элементы. Поэтому неизвестно какой элемент массива или произвольное значение можно принять за начальный минимум. Решение поставленной задачи можно разбить на два этапа: поиск положительных элементов в массиве с определением первого такого элемента и поиск среди положительных элементов минимального по значению. Блок-схема алгоритма приведена на рис. 5.2.4.

В нашем примере нумерация элементов массива начинается с единицы, поэтому в качестве начального значения для переменной imin принимается 0 (блок 1), т.е. значение которое не могут принимать индексы элементов массива Х. Таким образом показывается, что при обработке массива еще не встречался положительный элемент, который можно принять за начальное значение для минимума. Затем организовывается цикл по перебору всех элементов массива (блок 2). На каждом шаге цикла выполняется следующая последовательность действий.

В блоке 3 проверяется, не является ли текущий элемент массива X_i положительным. Если он отрицательный или равен нулю, то такой элемент пропускается и над ним не выполняется никаких действий. Если X_i > 0, то в блоке 4 проверяется, не является ли этот элемент первым встретившимся положительным элементом массива (признаком чего служит значение imin равное 0). В этом случае в блоке 5 переменной imin будет присвоено текущее значение i. Таким образом, за начальное значение для минимума будет принято значение первого по счету положительного элемента массива Х. Эта ситуация может возникнуть только один раз, и при дальнейшей работе цикла блок 5 больше выполняться не будет. Остальные положительные элементы массива в блоке 6 будут сравниваться с элементом массива, принятым в текущий момент за минимум. Если такой элемент окажется меньше минимального, то в блоке 7 в переменной imin будет сохранен его номер i.

После выхода из цикла проверяется, не равно ли значение imin нулю (блок 8), так как сразу же выводить значение минимального элемента массива X_imin и его номер imin (блок 9) нельзя. Это объясняется тем что, если в массиве Х не будет положительных элементов, то значение переменной imin останется равным нулю, а обращение к несуществующему элементу массива Х₀ не допустимо.
5.3. Сортировка элементов массива
Под сортировкой элементов массива понимается упорядочение элементов массива в порядке возрастания (убывания) их значений. Для этого необходимо организовать два вложенных цикла. Внешний цикл будет перебирать элементы, начиная с 1-го до предпоследнего, и выбирать так называемый «главный» элемент. Внутренний цикл будет перебирать элементы, начиная со следующего после текущего «главного» и до последнего.

Алгоритмы сортировки элементов массива по возрастанию или убыванию полностью идентичны и отличаются только проверяемым во внутреннем цикле условием. Поэтому в качестве примера рассмотрим алгоритм сортировки элементов массива по возрастанию их значений (рис. 5.3).

Внешний цикл «Для» на основе блока модификации (блок 1) по параметру i будет перебирать все элементы массива Х, начиная с первого и заканчивая предпоследним (N-1-ым) элементом. Для каждого выбранного во внешнем цикле «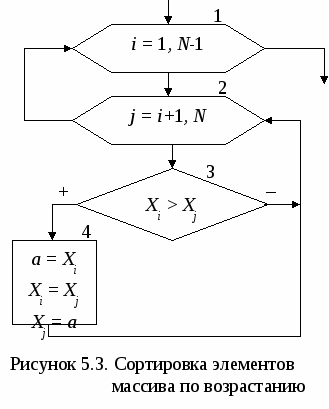
главного» элемента X_i организовывается внутренний цикл «Для» на основе блока модификации (блок 2), который будет перебирать элементы того же самого массива Х, только по параметру j. При этом перебираться будут элементы со следующего (i+1) после текущего «главного» элемента и заканчивая последним (N-ым) элементом. Таким образом, выбранный i-й элемент во внутреннем цикле (блок 3) поочередно будет сравниваться со всеми стоящими после него в массиве элементами (элементами с индексом j). Если «главный» i-й элемент оказывается больше, чем последующий j-й элемент, то их значения меняются местами (блок 4). Обмен значений двух элементов массива выполняется за 3 шага, с использованием дополнительной переменной a.

В процессе этих обменов в i-ю позицию будут выставляться все меньшие и меньшие значения. После завершения работы внутреннего цикла в i-м элементе массива будет находиться наименьшее, среди находящихся после «главного» элемента, значение. Затем во внешнем цикле выбирается следующий «главный» элемент, для которого выполняются те же самые действия и т.д. В итоге весь массив будет отсортирован в порядке возрастания значений его элементов.

Пусть массив Х состоит из четырех элементов {5; 7; 3; 2}. Пошаговое выполнение внутреннего цикла, при выбранном в качестве «главного» 1-го, а затем 2-го элементов массива, приведено ниже:

№ шага	X1	X2	X3	X4		№ шага	X1	X2	X3	X4
1	5	7	3	2		1	2	7	5	3
	↑i=1	↑j=2						↑i=2	↑j=3
2	5	7	3	2		2	2	5	7	3
	↑i=1		↑j=3					↑i=2		↑j=4
3	3	7	5	2		Итог	2	3	7	5
	↑i=1			↑ j=4
Итог	2	7	5	3

В итоге вначале в 1-й элемент массива занесено наименьшее значение. Затем во 2-й элемент массива занесено наименьшее среди оставшихся значение и т.д.

Для того чтобы этот алгоритм выполнял сортировку по убыванию достаточно в блоке 3 поменять знак больше на знак меньше.
5.4. Циклический сдвиг элементов массива
Под циклическим сдвигом понимается перестановка значений всех элементов массива на одну или несколько позиций влево или вправо. При этом значение первого (последнего) элемента массива заносится в последний (первый) элемент массива в зависимости от направления сдвига.

С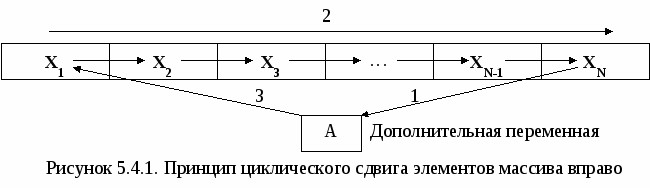хематичное изображение циклического сдвига элементов массива вправо на одну позицию, выполняемого в три этапа, показано на рис. 5.4.1. Блок-схема алгоритма, выполняющего такой сдвиг, показана на рис. 5.4.2.


На 1-м этапе значение последнего элемента массива X_N заносится в дополнительную переменную А (блок 1). На 2-м этапе организовывается цикл «Для» на основе блока модификации (блок 2), который перебирает элементы массива Х в обратном порядке, т.е. с правого края (шаг -1), начиная с N-го и заканчивая 2-м элементом. На каждом шаге цикла текущему элементу X_i присваивается значение предыдущего элемента X_i-1 (блок 3). В результате выполнения 2-го этапа значение предварительно сохраненного последнего элемента массива будет удалено. Значения остальных элементов массива будут смещены на одну позицию вправо. Значение первого элемента массива будет продублировано во втором элементе. На 3-м этапе алгоритма значение дополнительной переменной А, в которой хранится последний элемент исходного массива, будет занесено в первый элемент массива X₁. В итоге будет выполнен циклический сдвиг элементов массива Х на одну позицию вправо.

Следует обратить внимание на граничные значения параметра цикла i, который изменяется от N до 2. При подстановке этих значений в формулу сдвига не должно происходить обращение к несуществующим элементам массива. При i =N формула сдвига принимает вид X_N=X_{N -1}, при i=2 – X₂ =X₁. В случае если бы правая граница параметра i была равна 1, то в формуле сдвига происходило бы обращение к несуществующему элементу массива с индексом 0: X₁=X₀, что недопустимо.

С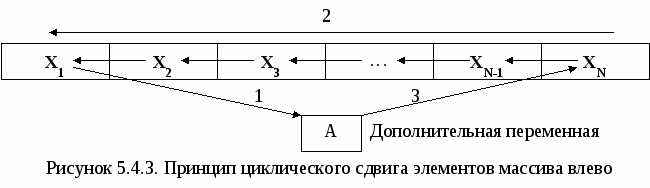хематичное изображение циклического сдвига элементов массива влево на одну позицию, также выполняемого в три этапа, показано на рис. 5.4.3. Блок-схема алгоритма, выполняющего такой сдвиг, показана на рис. 5.4.4.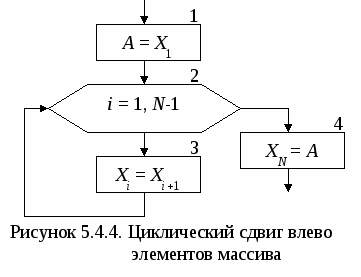




На 1-м этапе значение первого элемента массива X₁ заносится в дополнительную переменную А (блок 1). На 2-м этапе организовывается цикл «Для» (блок 2), который перебирает элементы массива Х в прямом порядке, т.е. с левого края (шаг +1), начиная с 1-го и заканчивая N-1-м элементом. На каждом шаге цикла текущему элементу X_i присваивается значение последующего элемента массива X_i+1 (блок 3). В результате выполнения 2-го этапа значение предварительно сохраненного первого элемента массива будет удалено. Значения остальных элементов массива будут смещены на одну позицию влево. Значение последнего элемента массива будет продублировано в предпоследнем элементе. На 3-м этапе алгоритма значение дополнительной переменной А, в которой хранится первый элемент исходного массива, будет занесено в последний элемент массива X_N. В итоге будет выполнен циклический сдвиг элементов массива Х на одну позицию влево.

Д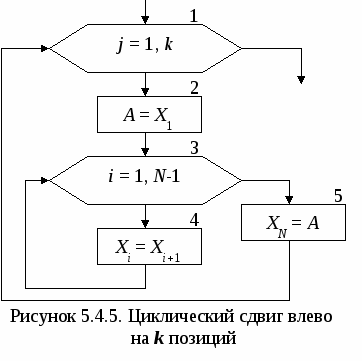ля выполнения циклического сдвига элементов массива на k позиций достаточно k раз выполнить алгоритм сдвига на одну позицию, т.е. добавить внешний цикл, который будет требуемое количество раз повторять сдвиг на одну позицию. Пример блок-схемы алгоритма, выполняющего циклический сдвиг элементов массива на k позиций влево, представлен на рис. 5.4.5.

Сдвиг элементов массива находит применение при удалении или добавлении элементов в массив, а также в других задачах.
5.5. Добавление и удаление элементов массива
Для добавления нового элемента массива необходимо выполнить следующую последовательность действий: увеличить размерность на единицу; сдвинуть вправо на одну позицию часть массива, начиная с позиции, в которую добавляется элемент; в «освободившийся» элемент записать добавляемое значение.

Пример 5.5.1. В массив Х размерностью N добавить новый элемент. Значение нового элемента и позиция, в которую он добавляется, указываются при вводе.

На рис. 5.5.1. приведен фрагмент блок-схемы алгоритма решения поставленной задачи. Процесс ввода и вывода массива Х не показан, т.к. он не отличается от описанного в п. 5.1.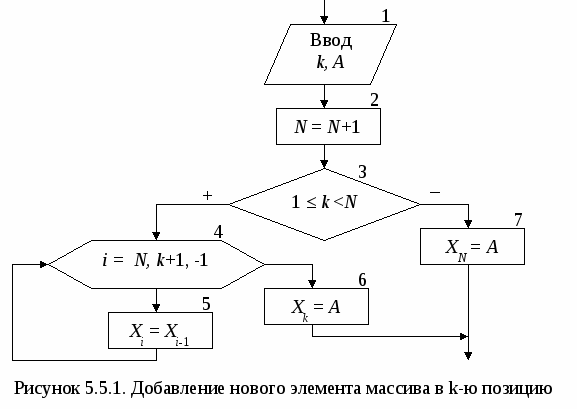



В блоке 1 в переменную А вводится значение нового элемента массива, а в переменную k заносится номер позиции, в которую он будет добавляться. После этого увеличивается размерность массива N на единицу (блок 2) и проверяется, действительно ли новый элемент добавляется в середину массива (блок 3). В этом случае производится сдвиг части элементов массива Х с N-й до k-й позиции вправо (блоки 4-5) и значение переменной А заносится в «освободившийся» элемент массива с номером k (блок 6). Если условие в блоке 3 не выполняется, то новый элемент добавляется в конец массива Х (блок 7).

Для удаления элемента из массива достаточно выполнить сдвиг части массива, расположенного после удаляемого, на одну позицию влево. В результате будет стерт удаляемый элемент, а последний элемент массива будет продублирован в предпоследний. После этого достаточно уменьшить размерность массива на единицу.

Пример 5.5.2. Из массива Х размерностью N удалить элемент с номером k. Номер удаляемого элемента указывается при вводе.

На рис. 5.5.2. показан фрагмент блок-схемы алгоритма решения поставленной задачи. При этом процесс ввода и вывода массива Х также не приводится.

В блоке 1 в переменную k вводится номер элемента, который необходимо удалить. В блоке 2 проверяется, находится ли удаляемый элемент в середине массива. В этом случае производится сдвиг части элементов массива Х с k-й до N-й позиции влево (блоки 3-4) и уменьшается размерность массива N на единицу (блок 7). В противном случае проверяется, не является ли удаляемый элемент последним в массиве (блок 5). Если это так, то для удаления элемента достаточно всего лишь уменьшить размерность массива N (блок 7). Если же значение k не удовлетворяет этим двум условием, значит, оно задано не верно и удаление элемента из массива не производится (блок 6).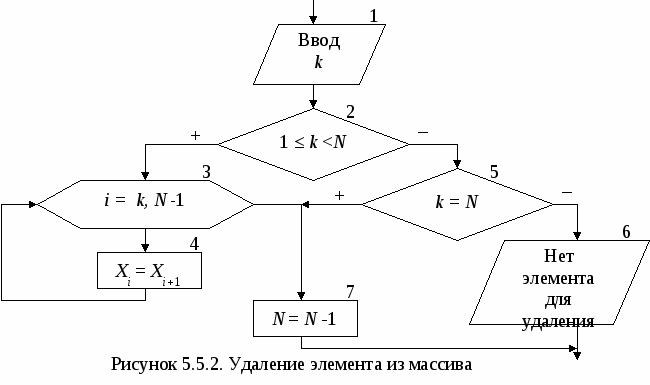



Иногда возникает необходимость удалить из массива не один, а несколько элементов, удовлетворяющих определенному условию (например, все элементы, значение которых равно 0). Для этой цели необходимо организовать два цикла по перебору элементов массива. Первый цикл (внешний) будет искать в массиве элементы, которые необходимо удалить. Второй цикл (внутренний) будет удалять найденные элементы, описанным выше способом. При этом для организации внешнего цикла не рекомендуется использовать цикл «Для». Это связано с тем, что после удаления элемента во внутреннем цикле, будет уменьшаться размерность массива, которая в свою очередь является граничным значением для параметра внешнего цикла.

На рис. 5.5.3. приводится фрагмент блок-схемы алгоритма, в котором выполняется удаление всех нулевых элементов из массива за один цикл.

Переменная k выполняет две функции: является счетчиком элементов массива, которые не надо удалять (не равные 0), и в тоже время задает позицию в массиве Х, в которую переставляется такой элемент (блок 1). В массиве осуществляется поиск (блоки 2-3) и подсчет количества элементов, которые не должны быть удалены (блок 4); каждый найденный элемент переставляется в начало массива в позицию, совпадающую с порядковым номером этого элемента (блок 4).




В результате все нулевые элементы массива будут пропущены, а элементы не равные 0 выставлены подряд в начало массива, размерность которого уже будет равна k(блок 5).
6. АЛГОРИТМЫ ОБРАБОТКИ ДВУМЕРНЫХ МАССИВОВ
Д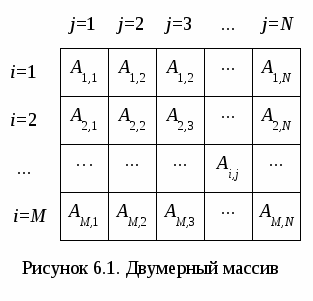
вумерный массив (матрица) представляет собой таблицу, на пересечении строк и столбцов которой располагаются элементы. Каждый элемент имеет два индекса. Первый индекс обычно обозначается буквой i и указывает номер строки, в которой расположен элемент. Второй индекс обозначается буквой j и указывает номер столбца, в котором расположен элемент (рис 6.1). Размерность двумерного массива задается двумя числами: M – количество строк и N – количество столбцов.

Двумерный массив, у которого количество строк равно количеству столбцов называется квадратной матрицей, в противном случае – прямоугольной.

Для обработки двумерного массива требуется два вложенных цикла, при этом наиболее удобно использовать циклы «Для» на основе блока модификации. Один будет перебирать строки, второй – столбцы массива. Таким образом, будут перебраны все элементы массива.

В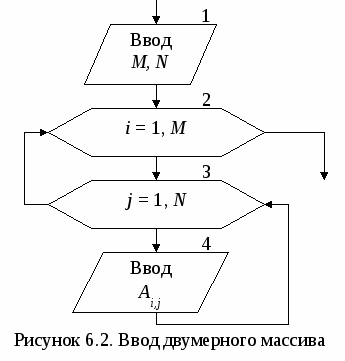
вод двумерного массива (рис. 6.2), также как и одномерного выполняется в два этапа. Вначале вводится размерность массива (блок 1), а затем значения для каждого элемента. Внешний цикл (блок 2) при i=1 «выбирает» 1-ю строку массива. Внутренний цикл (блок 3) перебирает все столбцы массива, т.е. поочередно выбираются элементы A_1,1, А_1,2, А_1,3 и т.д. до конца 1-й строки и вводятся их значения (блок 4). После выхода из внутреннего цикла происходит возврат в блок 2, где выбирается 2-я строка массива, для которой внутренний цикл опять переберет поочередно все элементы A_2,1, А_2,2, А_2,3 и т.д. Таким образом, элементы двумерного массива будут перебираться по строкам.

Аналогичным образом выполняется вывод элементов двумерного массива.

Если в блок-схеме на рис. 6.2. поменять местами параметры внешнего и внутреннего циклов, т.е. внешний цикл сделать по параметру j, а внутренний – по параметру i, то элементы массива будут перебираться по столбцам.

Пример 6.1. Сформировать вектор В размерностью M, каждый элемент которого равен количеству нулевых элементов соответствующей строки матрицы А размерностью M на N.

Как видно из условия количество элементов вектора В равно количеству строк матрицы А. Для решения поставленной задачи необходимо организовать построчный перебор элементов двумерного массива. Внешним должен быть цикл по параметру i, внутренним цикл по параметру j. Это даст возможность после завершения обработки каждой строки формировать элементы одномерного массива В. Блок-схема алгоритма приведена на рис. 6.3.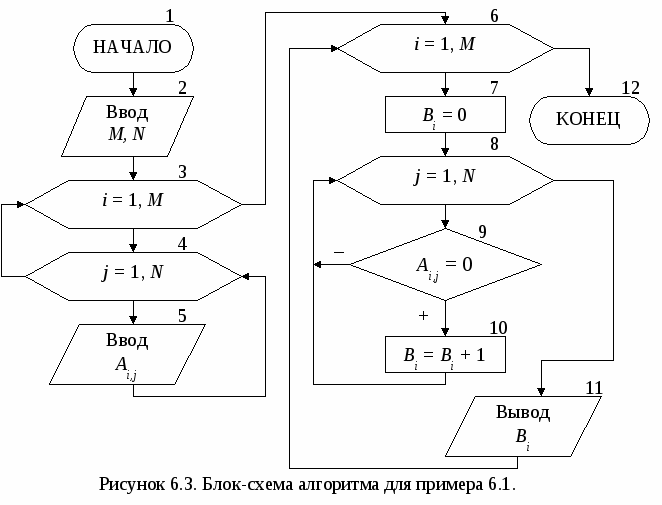



Блоки 2-5 вводят исходный двумерный массив А, описанным выше способом. Затем организовывается внешний цикл «Для» по параметру i на основе блока модификации (блок 6), который будет одновременно перебирать строки массива А и элементы одномерного массива В. С целью оптимизации алгоритма не вводится отдельная переменная для хранения количества нулевых элементов в каждой строке матрицы. Вместо неё будут использоваться непосредственно элементы массива В.

Для выбранной во внешнем цикле i-й строки обнуляется i-й элемент массива В (блок 7). Затем организовывается внутренний цикл «Для» по параметру j (блок 8), перебирающий столбцы массива А, т.е. элементы i-й строки. Каждый элемент проверяется на равенство нулю (блок 9), и в случае выполнения условия происходит увеличение счетчика нулевых элементов i-й строки, значение которого хранится в элементе B_i (блок 10). После завершения обработки строки (выхода из внутреннего цикла) происходит вывод i-го элемента массива В (блок 11) и переход к следующей строке. Обработав все строки двумерного массива А, алгоритм завершит свою работу.

Пример 6.2. Сформировать вектор В размерностью N, каждый элемент которого равен среднему арифметическому значению элементов соответствующего столбца матрицы А размерностью M на N.

В 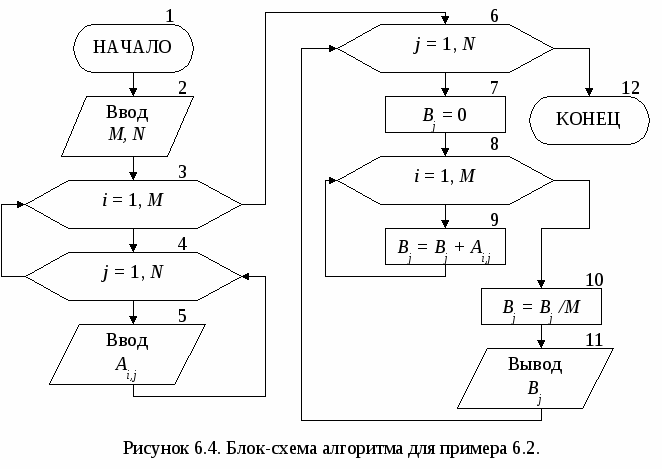данном примере количество элементов вектора В равно количеству столбцов матрицы А. Для решения задачи необходимо организовать перебор элементов двумерного массива по столбцам. Внешним должен быть цикл по параметру j, внутренним цикл по параметру i. Это даст возможность после завершения обработки каждого столбца вычислять соответствующие элементы одномерного массива В. Блок-схема алгоритма приведена на рис. 6.4.

Ввод элементов массива А осуществляется построчно (блоки 2-5). Во внешнем цикле по параметру j выбирается столбец массива А (блок 6), для него обнуляется значение суммы, которая будет хранится в соответствующем j-м элементе массива В (блок 7). Внутренний цикл по параметру i (блок 8) выполняет перебор и суммирование всех элементов текущего j-го столбца массива А (блок 9). После завершения работы внутреннего цикла в j-м элементе массива В вычисляется среднее арифметическое значение элементов j-го столбца массива А (блок 10), которое затем выводится (блок 11). На этом заканчивается тело внешнего цикла и происходит переход на его начало, где выбирается следующий столбец матрицы. Обработав все столбцы двумерного массива А, алгоритм завершит свою работу.

Принципы поиска максимального или минимального элементов в двумерных массивах ничем не отличаются от аналогичных принципов, используемых для одномерных массивов. Только в качестве параметров такого элемента определяются номера строки и столбца.

Пример 6.3. В каждой строке квадратной матрицы А размерностью N на N найти наибольший элемент и поменять его местами с элементом главной диагонали.

Главной диагональю квадратной матрицы называется диагональ, соединяющая верхний левый угол матрицы с правым нижним углом. Для элементов, расположенных на главной диагонали соблюдается соотношение между индексами: i=j. Для элементов расположенных ниже главной диагонали: i > j. Для элементов расположенных выше главной диагонали: i < j. Перебирая элементы матрицы и проверяя соотношения между индексами, всегда можно определить, где расположен текущий элемент.

В данной задаче необходимо организовать построчный перебор элементов матрицы. В каждой строке будем искать максимальный элемент, при этом для однозначного его определения достаточно хранить только номер столбца, в котором он находится в текущей строке. Блок-схема алгоритма приведена на рис. 6.5.

В блоках 2-5 вводится построчно квадратная матрица А размерностью N на N. Внешний цикл по параметру i (блок 6) выбирает текущую i-ю строку матрицы, в которой будет выполняться поиск максимального элемента. Вначале за максимум принимается первый элемент i-й строки (блок 7). Внутренний цикл перебирает элементы строки, начиная со второго (блок 8), и сравнивает их с элементом принятым за максимальный (блок 9). Если текущий элемент оказывается больше, чем принятый за максимум, то в переменной jmax запоминается его позиция в i-й строке, т.е. номер столбца, в котором этот элемент находится (блок 10). В противном случае текущий элемент пропускается. После выхода из внутреннего цикла в элемент главной диагонали A_i,i текущей i-й строки заносится значение максимального элемента этой строки A_i,jmax (блок 11). На этом заканчивается обработка текущей строки массива А (тело внешнего цикла) и происходит выбор следующей строки массива. После завершения обработки всех строк двумерного массива А, в блоках 12-14 выводится преобразованная матрица и алгоритм завершает свою работу.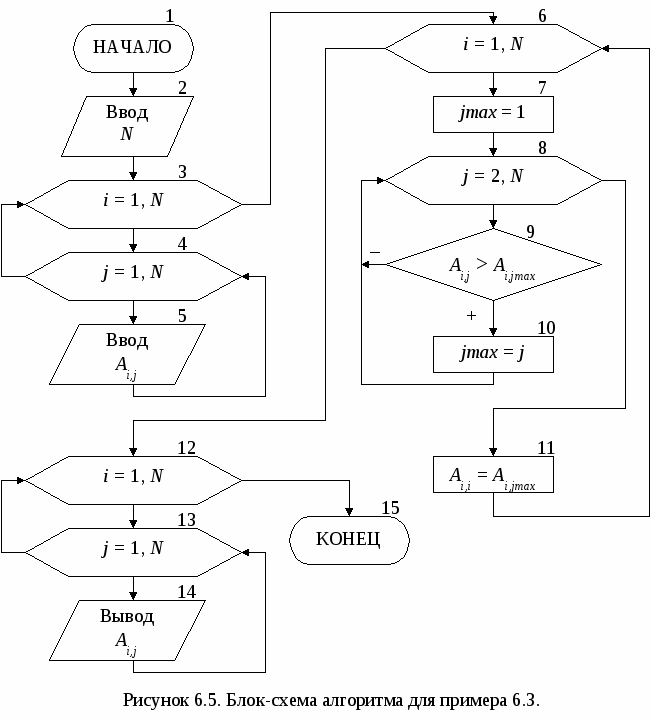



7. АЛГОРИТМЫ, СОДЕРЖАЩИЕ ВСПОМОГАТЕЛЬНЫЕ

ПОДЗАДАЧИ
При решении многих расчетных задачах возникает необходимость повторить несколько раз одну и ту же последовательность действий в разных частях алгоритма. В этом случае рационально выделить повторяющуюся последовательность действий в отдельную подзадачу – подпрограмму. Разработав алгоритм вспомогательной подзадачи, при составлении блок-схемы основного алгоритма необходимо предусмотреть обращение (вызов) к этой подзадаче.

Пример 7. Составить подпрограмму вычисления суммы элементов массива, которую использовать для обработки массивов A[Na], B[Nb]. Элементы массивов вычислять по формулам: A_r=0.3r²–1.2r; B_t=0.5t²+1.7t.

При решении поставленной задачи можно выделить несколько подзадач:

1. Подзадача вычисления (формирования) элементов исходных массивов А и В. Для этого следует обратить внимание на формульные зависимости по которым вычисляются элементы массивов и вывести общую зависимость. В нашем случае она будет иметь вид: X_i= k1i²+k2i.

2. Подзадача вывода элементов исходных массивов.

3. Подзадача вычисления суммы элементов массивов.

На рис. 7.1 приведена блок-схема алгоритма подзадачи вычисления элементов внутреннего одномерного массива Х. В качестве исходных данных в подзадачу передаются: массив Х, размерность массива M, коэффициенты k1 и k2.

На рис. 7.2 приведена блок-схема алгоритма подзадачи вывода элементов внутреннего массива Х. В качестве исходных данных в подзадачу передаются: массив Х, размерность массива M.



На рис. 7.3 приведена блок-схема алгоритма подзадачи вычисления суммы элементов внутреннего массива Х. В качестве исходных данных в подзадачу передаются: массив Х, размерность массива M. Результатом работы подзадачи будет вычисленное значение суммы элементов массива S.

На рис. 7.4 приведена блок-схема основного алгоритма решения задачи. Вначале алгоритма вводятся размерности обрабатываемых массивов А и В (блок 2). Блок 3 выполняет обращение к подпрограмме расчета элементов массива рр1 и передает в неё фактические параметры массива А и коэффициенты для формульной зависимости. После завершения работы подпрограммы рр1 в основной алгоритм будет возвращен сформированный массив А. Затем в блоке 4 выполняется вызов подпрограммы вывода элементов массива рр2, в которую также передаются фактические параметры массива А. Завершается обработка 1-го массива обращением к подпрограмме рр3 (блок 5), которая возвратит в переменную Sa значение вычисленной суммы элементов массива А.

Аналогичным образом в блоках 6-8 обрабатывается массив В. Завершает работу основного алгоритма вывод результирующих сумм Sa и Sb (блок 9).

Использование вспомогательных подзадач позволило избежать повторения одних и тех же по сути фрагментов блок-схемы алгоритма.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ